Paths to Equilibrium in Normal-Form Games

In multi-agent reinforcement learning (MARL), agents repeatedly interact across time and revise their strategies as new data arrives, producing a sequence of strategy profiles. This paper studies sequences of strategies satisfying a pairwise constraint inspired by policy updating in reinforcement learning, where an agent who is best responding in period $t$ does not switch its strategy in the next period $t+1$. This constraint merely requires that optimizing agents do not switch strategies, but does not constrain the other non-optimizing agents in any way, and thus allows for exploration. Sequences with this property are called satisficing paths, and arise naturally in many MARL algorithms. A fundamental question about strategic dynamics is such: for a given game and initial strategy profile, is it always possible to construct a satisficing path that terminates at an equilibrium strategy? The resolution of this question has implications about the capabilities or limitations of a class of MARL algorithms. We answer this question in the affirmative for mixed extensions of finite normal-form games.%

Asynchronous Decentralized Q-Learning: Two Timescale Analysis By Persistence

Non-stationarity is a fundamental challenge in multi-agent reinforcement learning (MARL), where agents update their behaviour as they learn. Many theoretical advances in MARL avoid the challenge of non-stationarity by coordinating the policy updates of agents in various ways, including synchronizing times at which agents are allowed to revise their policies. Synchronization enables analysis of many MARL algorithms via multi-timescale methods, but such synchrony is infeasible in many decentralized applications. In this paper, we study an asynchronous variant of the decentralized Q-learning algorithm, a recent MARL algorithm for stochastic games. We provide sufficient conditions under which the asynchronous algorithm drives play to equilibrium with high probability. Our solution utilizes constant learning rates in the Q-factor update, which we show to be critical for relaxing the synchrony assumptions of earlier work. Our analysis also applies to asynchronous generalizations of a number of other algorithms from the regret testing tradition, whose performance is analyzed by multi-timescale methods that study Markov chains obtained via policy update dynamics. This work extends the applicability of the decentralized Q-learning algorithm and its relatives to settings in which parameters are selected in an independent manner, and tames non-stationarity without imposing the coordination assumptions of prior work.

Decentralized Multi-Agent Reinforcement Learning for Continuous-Space Stochastic Games

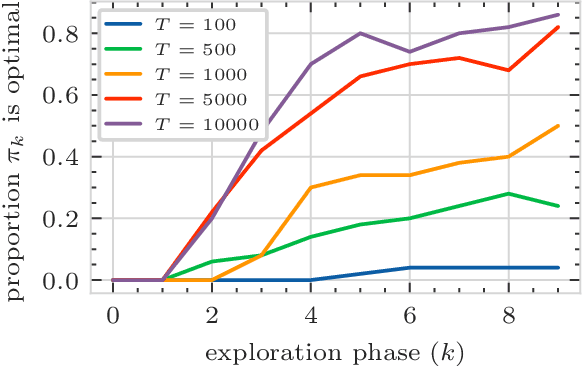
Stochastic games are a popular framework for studying multi-agent reinforcement learning (MARL). Recent advances in MARL have focused primarily on games with finitely many states. In this work, we study multi-agent learning in stochastic games with general state spaces and an information structure in which agents do not observe each other's actions. In this context, we propose a decentralized MARL algorithm and we prove the near-optimality of its policy updates. Furthermore, we study the global policy-updating dynamics for a general class of best-reply based algorithms and derive a closed-form characterization of convergence probabilities over the joint policy space.

An Independent Learning Algorithm for a Class of Symmetric Stochastic Games

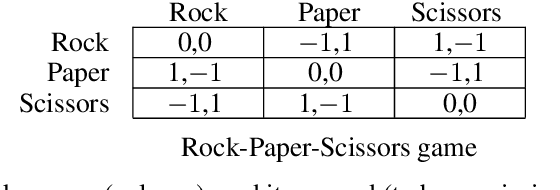
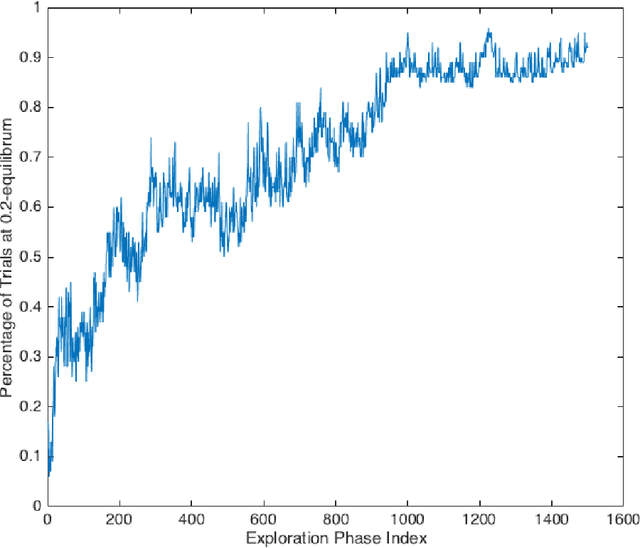
In multi-agent reinforcement learning, independent learners are those that do not access the action selections of other learning agents in the system. This paper investigates the feasibility of using independent learners to find approximate equilibrium policies in non-episodic, discounted stochastic games. We define a property, here called the $\epsilon$-revision paths property, and prove that a class of games exhibiting symmetry among the players has this property for any $\epsilon \geq 0$. Building on this result, we present an independent learning algorithm that comes with high probability guarantees of approximate equilibrium in this class of games. This guarantee is made assuming symmetry alone, without additional assumptions such as a zero sum, team, or potential game structure.