Paths to Equilibrium in Normal-Form Games

In multi-agent reinforcement learning (MARL), agents repeatedly interact across time and revise their strategies as new data arrives, producing a sequence of strategy profiles. This paper studies sequences of strategies satisfying a pairwise constraint inspired by policy updating in reinforcement learning, where an agent who is best responding in period $t$ does not switch its strategy in the next period $t+1$. This constraint merely requires that optimizing agents do not switch strategies, but does not constrain the other non-optimizing agents in any way, and thus allows for exploration. Sequences with this property are called satisficing paths, and arise naturally in many MARL algorithms. A fundamental question about strategic dynamics is such: for a given game and initial strategy profile, is it always possible to construct a satisficing path that terminates at an equilibrium strategy? The resolution of this question has implications about the capabilities or limitations of a class of MARL algorithms. We answer this question in the affirmative for mixed extensions of finite normal-form games.%

Recursive Reasoning in Minimax Games: A Level $k$ Gradient Play Method

Despite the success of generative adversarial networks (GANs) in generating visually appealing images, they are notoriously challenging to train. In order to stabilize the learning dynamics in minimax games, we propose a novel recursive reasoning algorithm: Level $k$ Gradient Play (Lv.$k$ GP) algorithm. In contrast to many existing algorithms, our algorithm does not require sophisticated heuristics or curvature information. We show that as $k$ increases, Lv.$k$ GP converges asymptotically towards an accurate estimation of players' future strategy. Moreover, we justify that Lv.$\infty$ GP naturally generalizes a line of provably convergent game dynamics which rely on predictive updates. Furthermore, we provide its local convergence property in nonconvex-nonconcave zero-sum games and global convergence in bilinear and quadratic games. By combining Lv.$k$ GP with Adam optimizer, our algorithm shows a clear advantage in terms of performance and computational overhead compared to other methods. Using a single Nvidia RTX3090 GPU and 30 times fewer parameters than BigGAN on CIFAR-10, we achieve an FID of 10.17 for unconditional image generation within 30 hours, allowing GAN training on common computational resources to reach state-of-the-art performance.

Second-Order Mirror Descent: Convergence in Games Beyond Averaging and Discounting

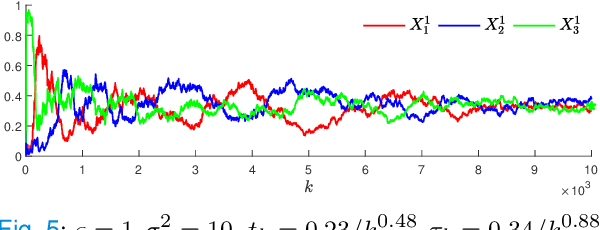
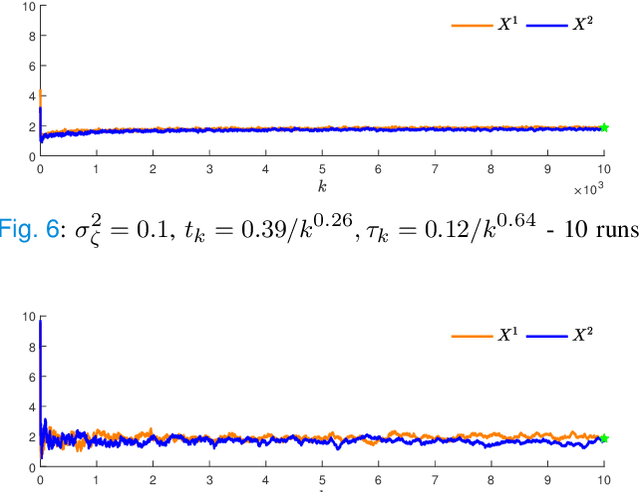
In this paper, we propose a second-order extension of the continuous-time game-theoretic mirror descent (MD) dynamics, referred to as MD2, which converges to mere (but not necessarily strict) variationally stable states (VSS) without using common auxiliary techniques such as averaging or discounting. We show that MD2 enjoys no-regret as well as exponential rate of convergence towards a strong VSS upon a slight modification. Furthermore, MD2 can be used to derive many novel primal-space dynamics. Lastly, using stochastic approximation techniques, we provide a convergence guarantee of discrete-time MD2 with noisy observations towards interior mere VSS. Selected simulations are provided to illustrate our results.

Continuous-time Discounted Mirror-Descent Dynamics in Monotone Concave Games

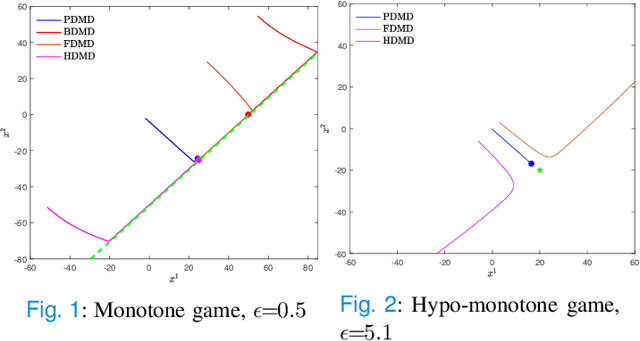
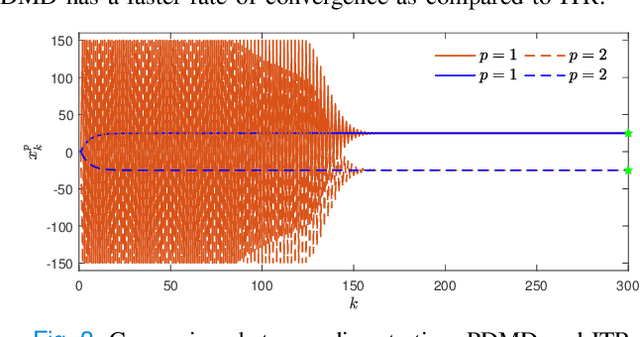
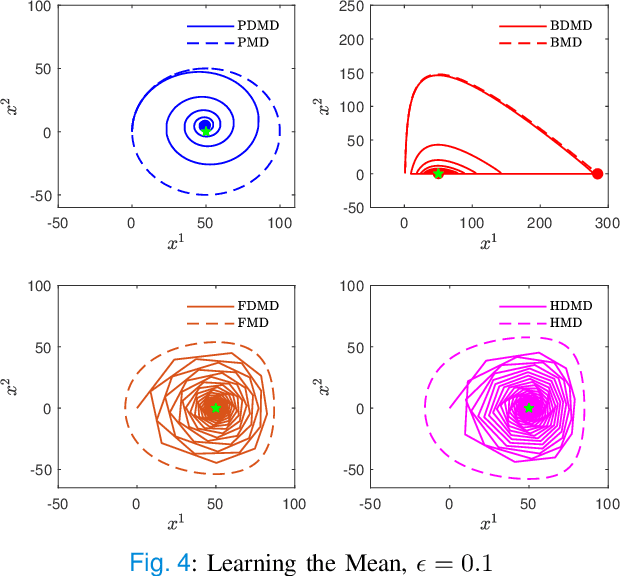
In this paper, we consider concave continuous-kernel games characterized by monotonicity properties and propose discounted mirror descent-type dynamics. We introduce two classes of dynamics whereby the associated mirror map is constructed based on a strongly convex or a Legendre regularizer. Depending on the properties of the regularizer we show that these new dynamics can converge asymptotically in concave games with monotone (negative) pseudo-gradient. Furthermore, we show that when the regularizer enjoys strong convexity, the resulting dynamics can converge even in games with hypo-monotone (negative) pseudo-gradient, which corresponds to a shortage of monotonicity.

From Game-theoretic Multi-agent Log Linear Learning to Reinforcement Learning

The main focus of this paper is on enhancement of two types of game-theoretic learning algorithms: log-linear learning and reinforcement learning. The standard analysis of log-linear learning needs a highly structured environment, i.e. strong assumptions about the game from an implementation perspective. In this paper, we introduce a variant of log-linear learning that provides asymptotic guarantees while relaxing the structural assumptions to include synchronous updates and limitations in information available to the players. On the other hand, model-free reinforcement learning is able to perform even under weaker assumptions on players' knowledge about the environment and other players' strategies. We propose a reinforcement algorithm that uses a double-aggregation scheme in order to deepen players' insight about the environment and constant learning step-size which achieves a higher convergence rate. Numerical experiments are conducted to verify each algorithm's robustness and performance.

On the Properties of the Softmax Function with Application in Game Theory and Reinforcement Learning

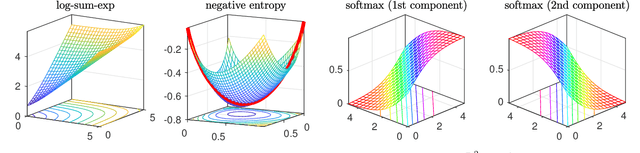
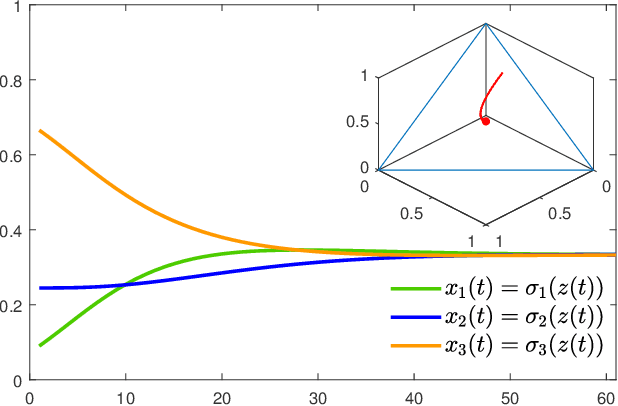
In this paper, we utilize results from convex analysis and monotone operator theory to derive additional properties of the softmax function that have not yet been covered in the existing literature. In particular, we show that the softmax function is the monotone gradient map of the log-sum-exp function. By exploiting this connection, we show that the inverse temperature parameter determines the Lipschitz and co-coercivity properties of the softmax function. We then demonstrate the usefulness of these properties through an application in game-theoretic reinforcement learning.