Second-Order Mirror Descent: Convergence in Games Beyond Averaging and Discounting

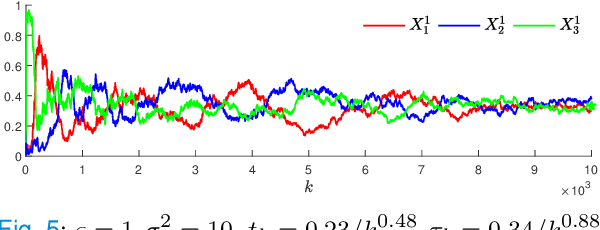
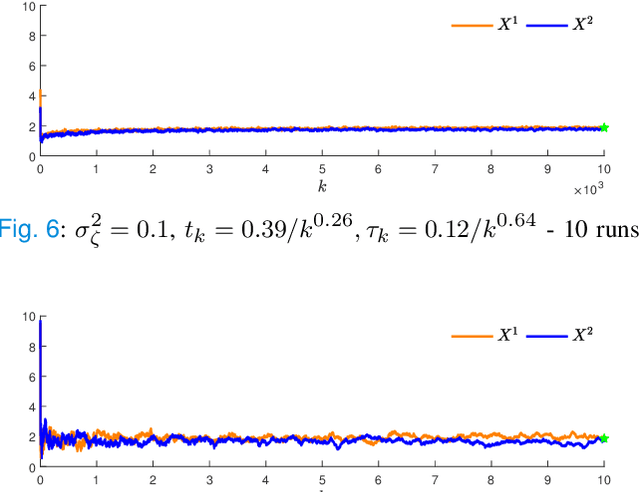
In this paper, we propose a second-order extension of the continuous-time game-theoretic mirror descent (MD) dynamics, referred to as MD2, which converges to mere (but not necessarily strict) variationally stable states (VSS) without using common auxiliary techniques such as averaging or discounting. We show that MD2 enjoys no-regret as well as exponential rate of convergence towards a strong VSS upon a slight modification. Furthermore, MD2 can be used to derive many novel primal-space dynamics. Lastly, using stochastic approximation techniques, we provide a convergence guarantee of discrete-time MD2 with noisy observations towards interior mere VSS. Selected simulations are provided to illustrate our results.