On the Properties of the Softmax Function with Application in Game Theory and Reinforcement Learning
Paper and Code
Aug 21, 2018
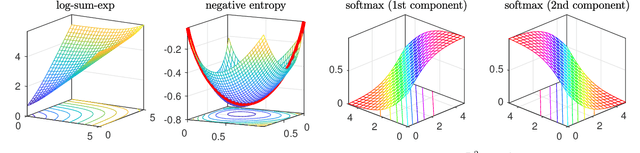
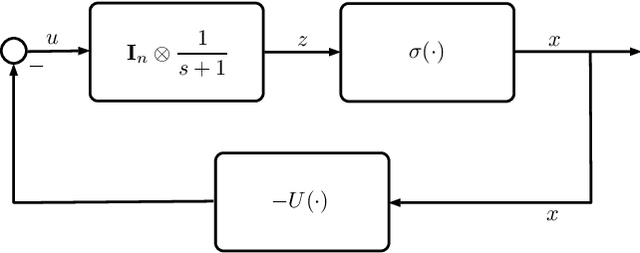
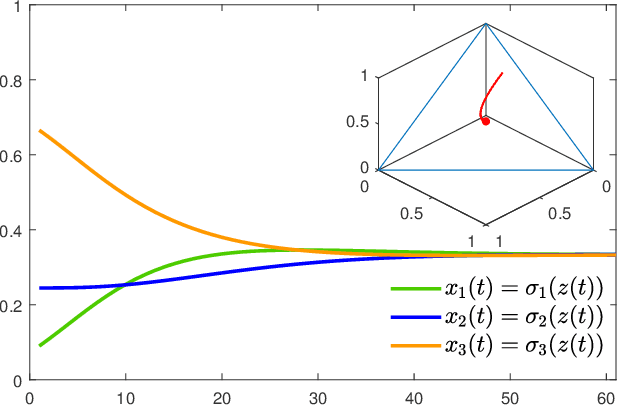
In this paper, we utilize results from convex analysis and monotone operator theory to derive additional properties of the softmax function that have not yet been covered in the existing literature. In particular, we show that the softmax function is the monotone gradient map of the log-sum-exp function. By exploiting this connection, we show that the inverse temperature parameter determines the Lipschitz and co-coercivity properties of the softmax function. We then demonstrate the usefulness of these properties through an application in game-theoretic reinforcement learning.
* 10 pages, 4 figures. Comments are welcome
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge