Paths to Equilibrium in Normal-Form Games

In multi-agent reinforcement learning (MARL), agents repeatedly interact across time and revise their strategies as new data arrives, producing a sequence of strategy profiles. This paper studies sequences of strategies satisfying a pairwise constraint inspired by policy updating in reinforcement learning, where an agent who is best responding in period $t$ does not switch its strategy in the next period $t+1$. This constraint merely requires that optimizing agents do not switch strategies, but does not constrain the other non-optimizing agents in any way, and thus allows for exploration. Sequences with this property are called satisficing paths, and arise naturally in many MARL algorithms. A fundamental question about strategic dynamics is such: for a given game and initial strategy profile, is it always possible to construct a satisficing path that terminates at an equilibrium strategy? The resolution of this question has implications about the capabilities or limitations of a class of MARL algorithms. We answer this question in the affirmative for mixed extensions of finite normal-form games.%

Asynchronous Decentralized Q-Learning: Two Timescale Analysis By Persistence

Non-stationarity is a fundamental challenge in multi-agent reinforcement learning (MARL), where agents update their behaviour as they learn. Many theoretical advances in MARL avoid the challenge of non-stationarity by coordinating the policy updates of agents in various ways, including synchronizing times at which agents are allowed to revise their policies. Synchronization enables analysis of many MARL algorithms via multi-timescale methods, but such synchrony is infeasible in many decentralized applications. In this paper, we study an asynchronous variant of the decentralized Q-learning algorithm, a recent MARL algorithm for stochastic games. We provide sufficient conditions under which the asynchronous algorithm drives play to equilibrium with high probability. Our solution utilizes constant learning rates in the Q-factor update, which we show to be critical for relaxing the synchrony assumptions of earlier work. Our analysis also applies to asynchronous generalizations of a number of other algorithms from the regret testing tradition, whose performance is analyzed by multi-timescale methods that study Markov chains obtained via policy update dynamics. This work extends the applicability of the decentralized Q-learning algorithm and its relatives to settings in which parameters are selected in an independent manner, and tames non-stationarity without imposing the coordination assumptions of prior work.

An Independent Learning Algorithm for a Class of Symmetric Stochastic Games

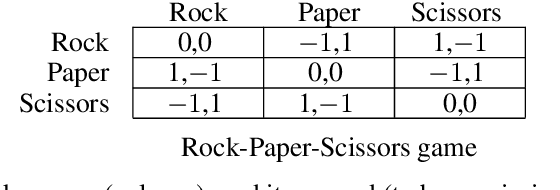
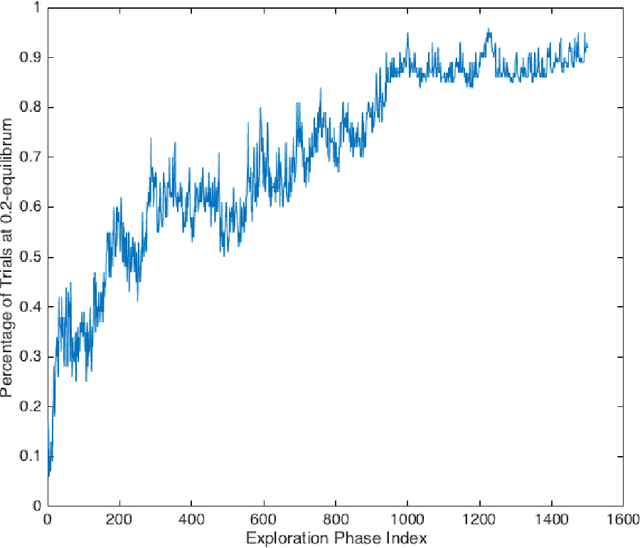
In multi-agent reinforcement learning, independent learners are those that do not access the action selections of other learning agents in the system. This paper investigates the feasibility of using independent learners to find approximate equilibrium policies in non-episodic, discounted stochastic games. We define a property, here called the $\epsilon$-revision paths property, and prove that a class of games exhibiting symmetry among the players has this property for any $\epsilon \geq 0$. Building on this result, we present an independent learning algorithm that comes with high probability guarantees of approximate equilibrium in this class of games. This guarantee is made assuming symmetry alone, without additional assumptions such as a zero sum, team, or potential game structure.

Decentralized Q-Learning for Stochastic Teams and Games

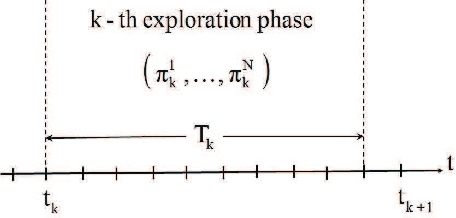
There are only a few learning algorithms applicable to stochastic dynamic teams and games which generalize Markov decision processes to decentralized stochastic control problems involving possibly self-interested decision makers. Learning in games is generally difficult because of the non-stationary environment in which each decision maker aims to learn its optimal decisions with minimal information in the presence of the other decision makers who are also learning. In stochastic dynamic games, learning is more challenging because, while learning, the decision makers alter the state of the system and hence the future cost. In this paper, we present decentralized Q-learning algorithms for stochastic games, and study their convergence for the weakly acyclic case which includes team problems as an important special case. The algorithm is decentralized in that each decision maker has access to only its local information, the state information, and the local cost realizations; furthermore, it is completely oblivious to the presence of other decision makers. We show that these algorithms converge to equilibrium policies almost surely in large classes of stochastic games.