An Independent Learning Algorithm for a Class of Symmetric Stochastic Games
Paper and Code
Oct 09, 2021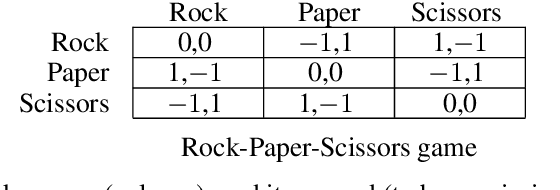

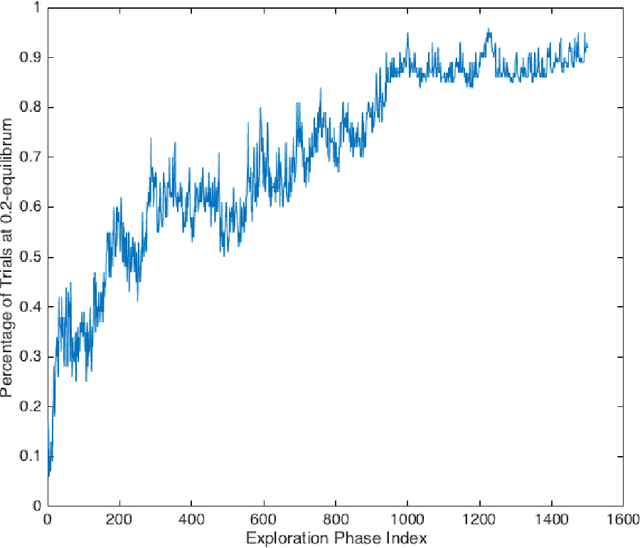
In multi-agent reinforcement learning, independent learners are those that do not access the action selections of other learning agents in the system. This paper investigates the feasibility of using independent learners to find approximate equilibrium policies in non-episodic, discounted stochastic games. We define a property, here called the $\epsilon$-revision paths property, and prove that a class of games exhibiting symmetry among the players has this property for any $\epsilon \geq 0$. Building on this result, we present an independent learning algorithm that comes with high probability guarantees of approximate equilibrium in this class of games. This guarantee is made assuming symmetry alone, without additional assumptions such as a zero sum, team, or potential game structure.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge