Continuous-time Discounted Mirror-Descent Dynamics in Monotone Concave Games

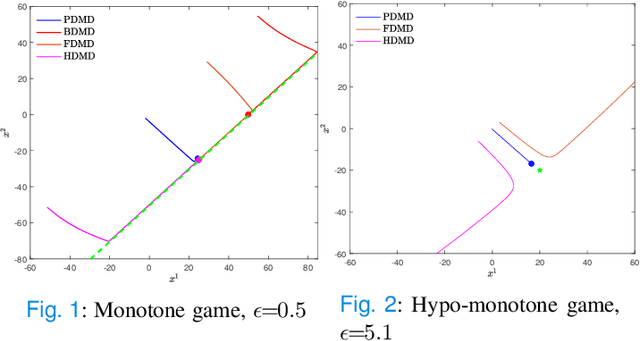
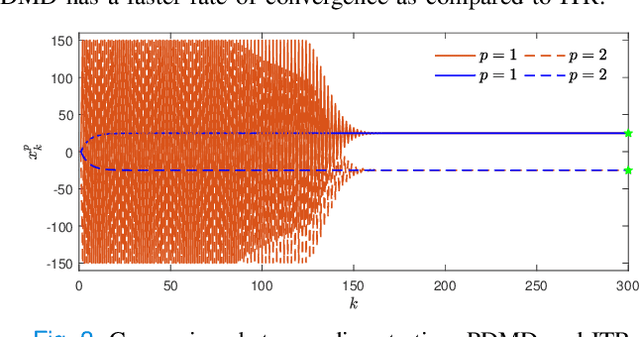
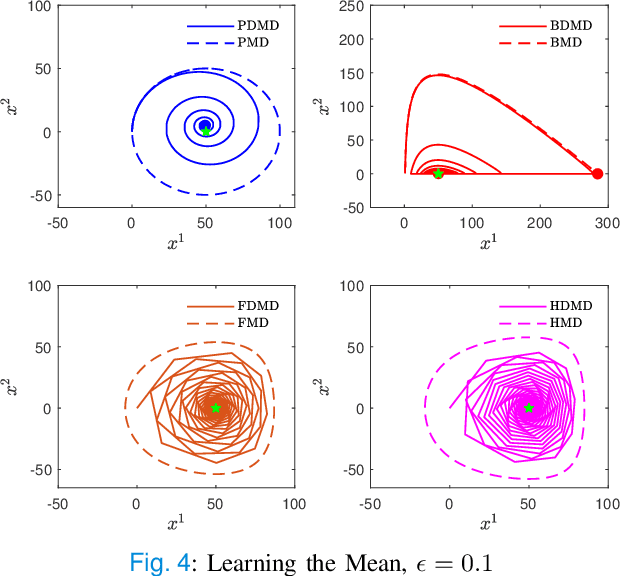
In this paper, we consider concave continuous-kernel games characterized by monotonicity properties and propose discounted mirror descent-type dynamics. We introduce two classes of dynamics whereby the associated mirror map is constructed based on a strongly convex or a Legendre regularizer. Depending on the properties of the regularizer we show that these new dynamics can converge asymptotically in concave games with monotone (negative) pseudo-gradient. Furthermore, we show that when the regularizer enjoys strong convexity, the resulting dynamics can converge even in games with hypo-monotone (negative) pseudo-gradient, which corresponds to a shortage of monotonicity.