Decentralized Multi-Agent Reinforcement Learning for Continuous-Space Stochastic Games
Paper and Code
Mar 16, 2023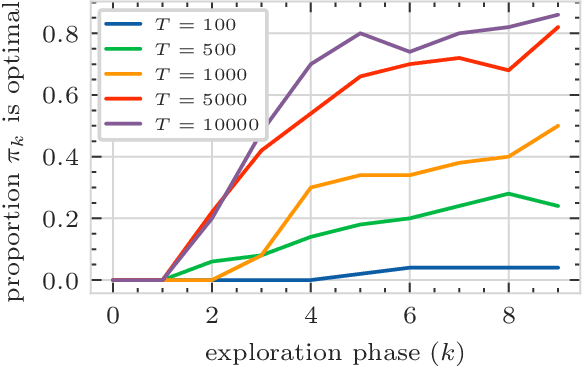
Stochastic games are a popular framework for studying multi-agent reinforcement learning (MARL). Recent advances in MARL have focused primarily on games with finitely many states. In this work, we study multi-agent learning in stochastic games with general state spaces and an information structure in which agents do not observe each other's actions. In this context, we propose a decentralized MARL algorithm and we prove the near-optimality of its policy updates. Furthermore, we study the global policy-updating dynamics for a general class of best-reply based algorithms and derive a closed-form characterization of convergence probabilities over the joint policy space.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge