On the Role of Information Structure in Reinforcement Learning for Partially-Observable Sequential Teams and Games

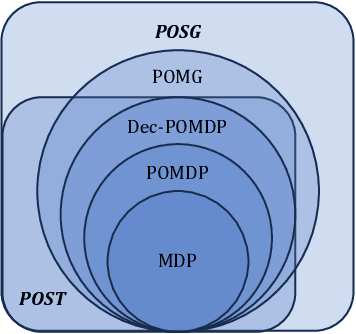
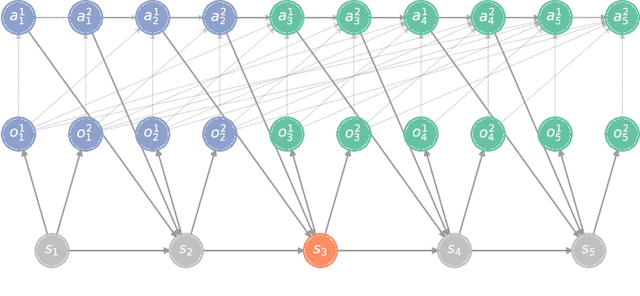
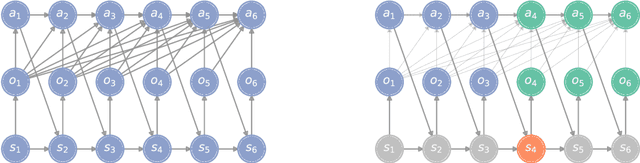
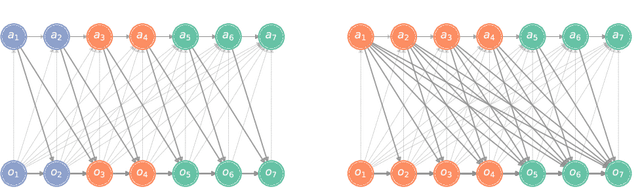
In a sequential decision-making problem, the information structure is the description of how events in the system occurring at different points in time affect each other. Classical models of reinforcement learning (e.g., MDPs, POMDPs, Dec-POMDPs, and POMGs) assume a very simple and highly regular information structure, while more general models like predictive state representations do not explicitly model the information structure. By contrast, real-world sequential decision-making problems typically involve a complex and time-varying interdependence of system variables, requiring a rich and flexible representation of information structure. In this paper, we argue for the perspective that explicit representation of information structures is an important component of analyzing and solving reinforcement learning problems. We propose novel reinforcement learning models with an explicit representation of information structure, capturing classical models as special cases. We show that this leads to a richer analysis of sequential decision-making problems and enables more tailored algorithm design. In particular, we characterize the "complexity" of the observable dynamics of any sequential decision-making problem through a graph-theoretic analysis of the DAG representation of its information structure. The central quantity in this analysis is the minimal set of variables that $d$-separates the past observations from future observations. Furthermore, through constructing a generalization of predictive state representations, we propose tailored reinforcement learning algorithms and prove that the sample complexity is in part determined by the information structure. This recovers known tractability results and gives a novel perspective on reinforcement learning in general sequential decision-making problems, providing a systematic way of identifying new tractable classes of problems.