Paraformer: Parameterization of Sub-grid Scale Processes Using Transformers

One of the major sources of uncertainty in the current generation of Global Climate Models (GCMs) is the representation of sub-grid scale physical processes. Over the years, a series of deep-learning-based parameterization schemes have been developed and tested on both idealized and real-geography GCMs. However, datasets on which previous deep-learning models were trained either contain limited variables or have low spatial-temporal coverage, which can not fully simulate the parameterization process. Additionally, these schemes rely on classical architectures while the latest attention mechanism used in Transformer models remains unexplored in this field. In this paper, we propose Paraformer, a "memory-aware" Transformer-based model on ClimSim, the largest dataset ever created for climate parameterization. Our results demonstrate that the proposed model successfully captures the complex non-linear dependencies in the sub-grid scale variables and outperforms classical deep-learning architectures. This work highlights the applicability of the attenuation mechanism in this field and provides valuable insights for developing future deep-learning-based climate parameterization schemes.

CDA: Contrastive-adversarial Domain Adaptation

Recent advances in domain adaptation reveal that adversarial learning on deep neural networks can learn domain invariant features to reduce the shift between source and target domains. While such adversarial approaches achieve domain-level alignment, they ignore the class (label) shift. When class-conditional data distributions are significantly different between the source and target domain, it can generate ambiguous features near class boundaries that are more likely to be misclassified. In this work, we propose a two-stage model for domain adaptation called \textbf{C}ontrastive-adversarial \textbf{D}omain \textbf{A}daptation \textbf{(CDA)}. While the adversarial component facilitates domain-level alignment, two-stage contrastive learning exploits class information to achieve higher intra-class compactness across domains resulting in well-separated decision boundaries. Furthermore, the proposed contrastive framework is designed as a plug-and-play module that can be easily embedded with existing adversarial methods for domain adaptation. We conduct experiments on two widely used benchmark datasets for domain adaptation, namely, \textit{Office-31} and \textit{Digits-5}, and demonstrate that CDA achieves state-of-the-art results on both datasets.

Robust Causality and False Attribution in Data-Driven Earth Science Discoveries

Causal and attribution studies are essential for earth scientific discoveries and critical for informing climate, ecology, and water policies. However, the current generation of methods needs to keep pace with the complexity of scientific and stakeholder challenges and data availability combined with the adequacy of data-driven methods. Unless carefully informed by physics, they run the risk of conflating correlation with causation or getting overwhelmed by estimation inaccuracies. Given that natural experiments, controlled trials, interventions, and counterfactual examinations are often impractical, information-theoretic methods have been developed and are being continually refined in the earth sciences. Here we show that transfer entropy-based causal graphs, which have recently become popular in the earth sciences with high-profile discoveries, can be spurious even when augmented with statistical significance. We develop a subsample-based ensemble approach for robust causality analysis. Simulated data, and observations in climate and ecohydrology, suggest the robustness and consistency of this approach.

Deep Transfer Learning on Satellite Imagery Improves Air Quality Estimates in Developing Nations

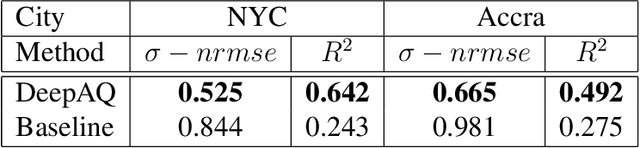
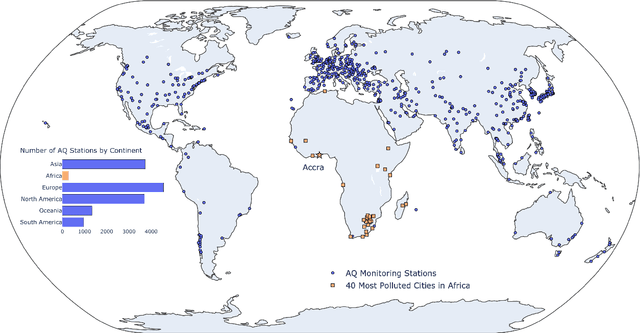
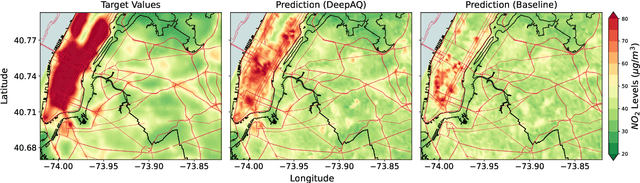
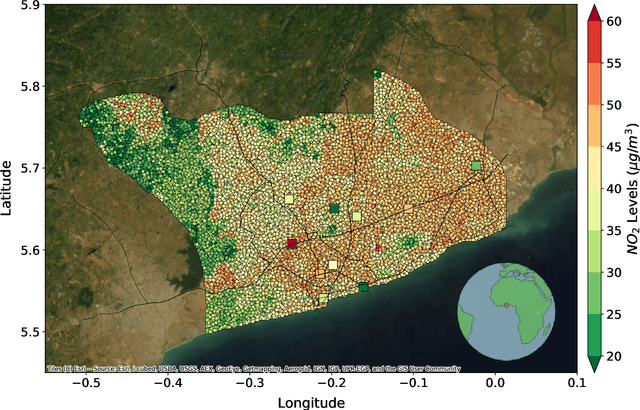
Urban air pollution is a public health challenge in low- and middle-income countries (LMICs). However, LMICs lack adequate air quality (AQ) monitoring infrastructure. A persistent challenge has been our inability to estimate AQ accurately in LMIC cities, which hinders emergency preparedness and risk mitigation. Deep learning-based models that map satellite imagery to AQ can be built for high-income countries (HICs) with adequate ground data. Here we demonstrate that a scalable approach that adapts deep transfer learning on satellite imagery for AQ can extract meaningful estimates and insights in LMIC cities based on spatiotemporal patterns learned in HIC cities. The approach is demonstrated for Accra in Ghana, Africa, with AQ patterns learned from two US cities, specifically Los Angeles and New York.

Explainable deep learning for insights in El Nino and river flows

The El Nino Southern Oscillation (ENSO) is a semi-periodic fluctuation in sea surface temperature (SST) over the tropical central and eastern Pacific Ocean that influences interannual variability in regional hydrology across the world through long-range dependence or teleconnections. Recent research has demonstrated the value of Deep Learning (DL) methods for improving ENSO prediction as well as Complex Networks (CN) for understanding teleconnections. However, gaps in predictive understanding of ENSO-driven river flows include the black box nature of DL, the use of simple ENSO indices to describe a complex phenomenon and translating DL-based ENSO predictions to river flow predictions. Here we show that eXplainable DL (XDL) methods, based on saliency maps, can extract interpretable predictive information contained in global SST and discover novel SST information regions and dependence structures relevant for river flows which, in tandem with climate network constructions, enable improved predictive understanding. Our results reveal additional information content in global SST beyond ENSO indices, develop new understanding of how SSTs influence river flows, and generate improved river flow predictions with uncertainties. Observations, reanalysis data, and earth system model simulations are used to demonstrate the value of the XDL-CN based methods for future interannual and decadal scale climate projections.

Bayesian Deep Learning Hyperparameter Search for Robust Function Mapping to Polynomials with Noise

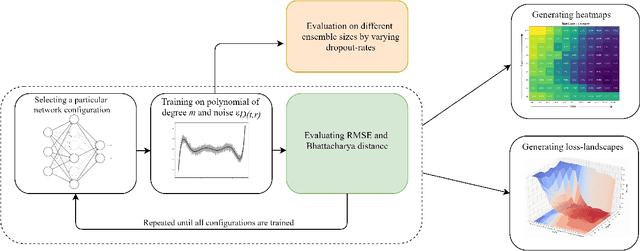
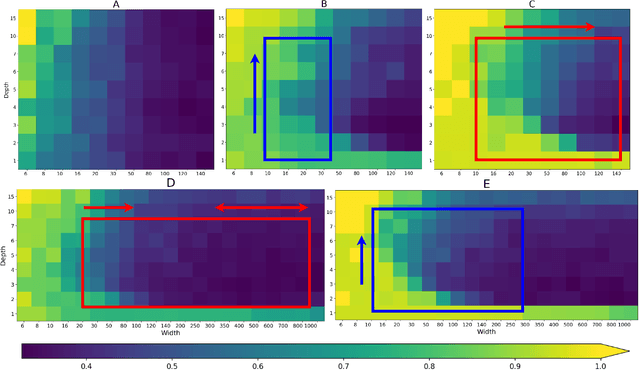
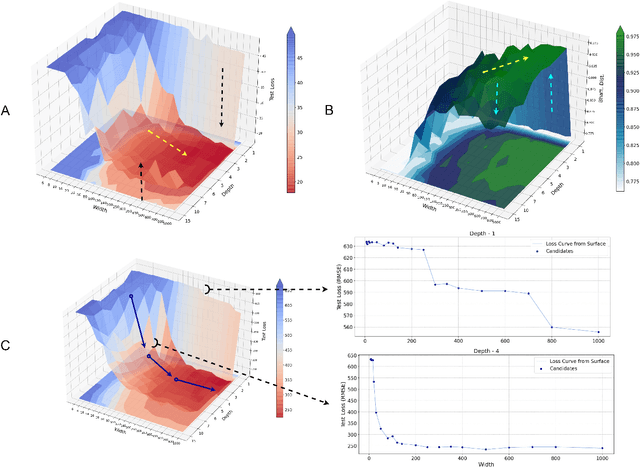
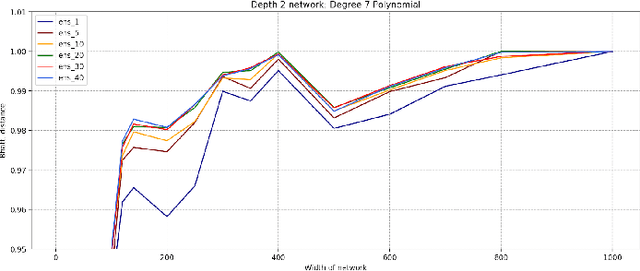
Advances in neural architecture search, as well as explainability and interpretability of connectionist architectures, have been reported in the recent literature. However, our understanding of how to design Bayesian Deep Learning (BDL) hyperparameters, specifically, the depth, width and ensemble size, for robust function mapping with uncertainty quantification, is still emerging. This paper attempts to further our understanding by mapping Bayesian connectionist representations to polynomials of different orders with varying noise types and ratios. We examine the noise-contaminated polynomials to search for the combination of hyperparameters that can extract the underlying polynomial signals while quantifying uncertainties based on the noise attributes. Specifically, we attempt to study the question that an appropriate neural architecture and ensemble configuration can be found to detect a signal of any n-th order polynomial contaminated with noise having different distributions and signal-to-noise (SNR) ratios and varying noise attributes. Our results suggest the possible existence of an optimal network depth as well as an optimal number of ensembles for prediction skills and uncertainty quantification, respectively. However, optimality is not discernible for width, even though the performance gain reduces with increasing width at high values of width. Our experiments and insights can be directional to understand theoretical properties of BDL representations and to design practical solutions.

Machine Learning for Robust Identification of Complex Nonlinear Dynamical Systems: Applications to Earth Systems Modeling

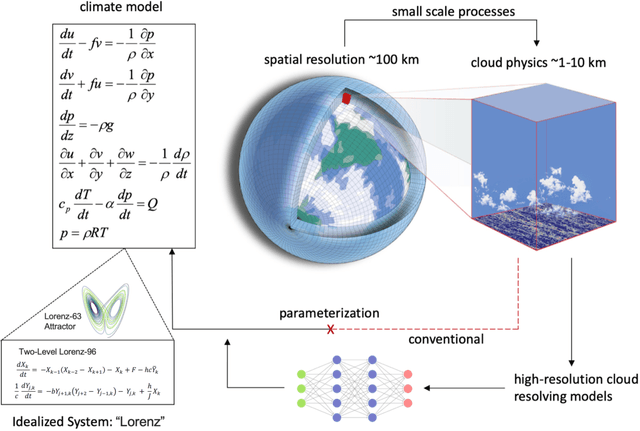
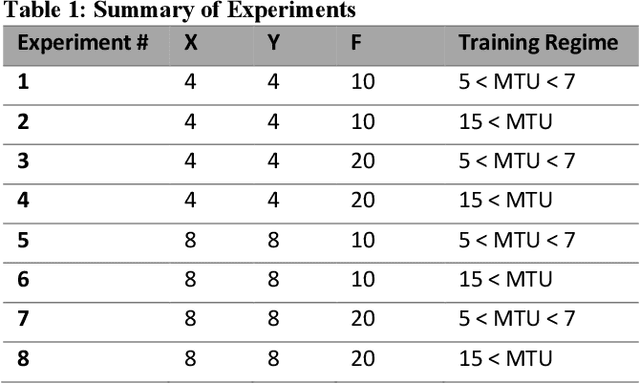
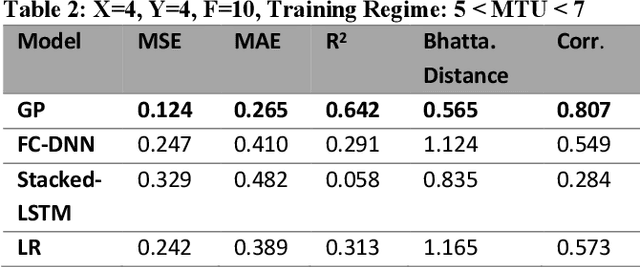
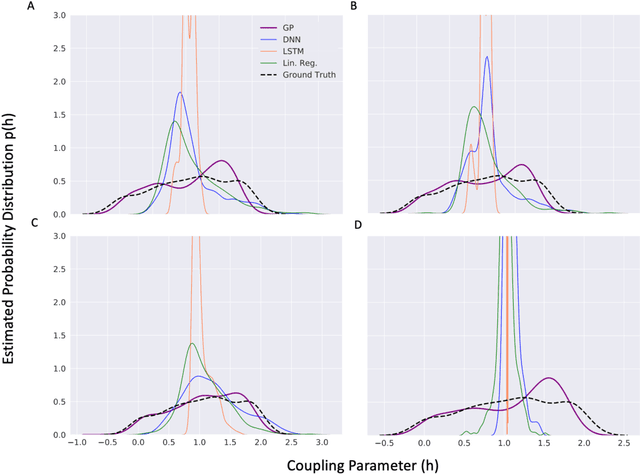
Systems exhibiting nonlinear dynamics, including but not limited to chaos, are ubiquitous across Earth Sciences such as Meteorology, Hydrology, Climate and Ecology, as well as Biology such as neural and cardiac processes. However, System Identification remains a challenge. In climate and earth systems models, while governing equations follow from first principles and understanding of key processes has steadily improved, the largest uncertainties are often caused by parameterizations such as cloud physics, which in turn have witnessed limited improvements over the last several decades. Climate scientists have pointed to Machine Learning enhanced parameter estimation as a possible solution, with proof-of-concept methodological adaptations being examined on idealized systems. While climate science has been highlighted as a "Big Data" challenge owing to the volume and complexity of archived model-simulations and observations from remote and in-situ sensors, the parameter estimation process is often relatively a "small data" problem. A crucial question for data scientists in this context is the relevance of state-of-the-art data-driven approaches including those based on deep neural networks or kernel-based processes. Here we consider a chaotic system - two-level Lorenz-96 - used as a benchmark model in the climate science literature, adopt a methodology based on Gaussian Processes for parameter estimation and compare the gains in predictive understanding with a suite of Deep Learning and strawman Linear Regression methods. Our results show that adaptations of kernel-based Gaussian Processes can outperform other approaches under small data constraints along with uncertainty quantification; and needs to be considered as a viable approach in climate science and earth system modeling.

Deep Learning Emulation of Multi-Angle Implementation of Atmospheric Correction (MAIAC)

New generation geostationary satellites make solar reflectance observations available at a continental scale with unprecedented spatiotemporal resolution and spectral range. Generating quality land monitoring products requires correction of the effects of atmospheric scattering and absorption, which vary in time and space according to geometry and atmospheric composition. Many atmospheric radiative transfer models, including that of Multi-Angle Implementation of Atmospheric Correction (MAIAC), are too computationally complex to be run in real time, and rely on precomputed look-up tables. Additionally, uncertainty in measurements and models for remote sensing receives insufficient attention, in part due to the difficulty of obtaining sufficient ground measurements. In this paper, we present an adaptation of Bayesian Deep Learning (BDL) to emulation of the MAIAC atmospheric correction algorithm. Emulation approaches learn a statistical model as an efficient approximation of a physical model, while machine learning methods have demonstrated performance in extracting spatial features and learning complex, nonlinear mappings. We demonstrate stable surface reflectance retrieval by emulation (R2 between MAIAC and emulator SR are 0.63, 0.75, 0.86, 0.84, 0.95, and 0.91 for Blue, Green, Red, NIR, SWIR1, and SWIR2 bands, respectively), accurate cloud detection (86\%), and well-calibrated, geolocated uncertainty estimates. Our results support BDL-based emulation as an accurate and efficient (up to 6x speedup) method for approximation atmospheric correction, where built-in uncertainty estimates stand to open new opportunities for model assessment and support informed use of SR-derived quantities in multiple domains.

Quantifying Uncertainty in Discrete-Continuous and Skewed Data with Bayesian Deep Learning

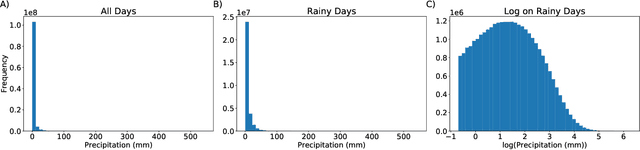
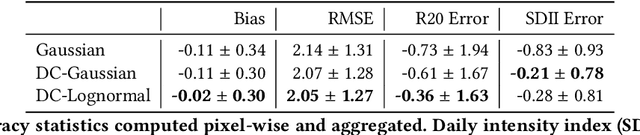
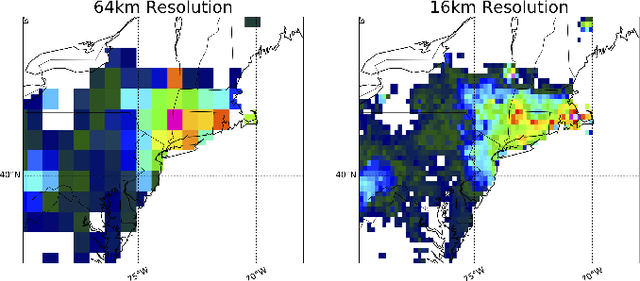
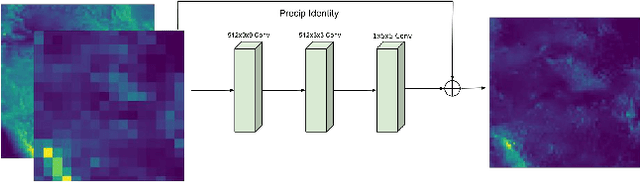
Deep Learning (DL) methods have been transforming computer vision with innovative adaptations to other domains including climate change. For DL to pervade Science and Engineering (S&E) applications where risk management is a core component, well-characterized uncertainty estimates must accompany predictions. However, S&E observations and model-simulations often follow heavily skewed distributions and are not well modeled with DL approaches, since they usually optimize a Gaussian, or Euclidean, likelihood loss. Recent developments in Bayesian Deep Learning (BDL), which attempts to capture uncertainties from noisy observations, aleatoric, and from unknown model parameters, epistemic, provide us a foundation. Here we present a discrete-continuous BDL model with Gaussian and lognormal likelihoods for uncertainty quantification (UQ). We demonstrate the approach by developing UQ estimates on `DeepSD', a super-resolution based DL model for Statistical Downscaling (SD) in climate applied to precipitation, which follows an extremely skewed distribution. We find that the discrete-continuous models outperform a basic Gaussian distribution in terms of predictive accuracy and uncertainty calibration. Furthermore, we find that the lognormal distribution, which can handle skewed distributions, produces quality uncertainty estimates at the extremes. Such results may be important across S&E, as well as other domains such as finance and economics, where extremes are often of significant interest. Furthermore, to our knowledge, this is the first UQ model in SD where both aleatoric and epistemic uncertainties are characterized.