Quantifying Uncertainty in Discrete-Continuous and Skewed Data with Bayesian Deep Learning

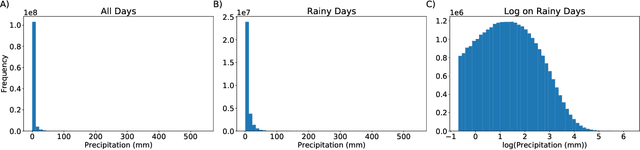
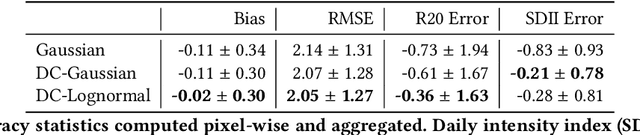
Deep Learning (DL) methods have been transforming computer vision with innovative adaptations to other domains including climate change. For DL to pervade Science and Engineering (S&E) applications where risk management is a core component, well-characterized uncertainty estimates must accompany predictions. However, S&E observations and model-simulations often follow heavily skewed distributions and are not well modeled with DL approaches, since they usually optimize a Gaussian, or Euclidean, likelihood loss. Recent developments in Bayesian Deep Learning (BDL), which attempts to capture uncertainties from noisy observations, aleatoric, and from unknown model parameters, epistemic, provide us a foundation. Here we present a discrete-continuous BDL model with Gaussian and lognormal likelihoods for uncertainty quantification (UQ). We demonstrate the approach by developing UQ estimates on `DeepSD', a super-resolution based DL model for Statistical Downscaling (SD) in climate applied to precipitation, which follows an extremely skewed distribution. We find that the discrete-continuous models outperform a basic Gaussian distribution in terms of predictive accuracy and uncertainty calibration. Furthermore, we find that the lognormal distribution, which can handle skewed distributions, produces quality uncertainty estimates at the extremes. Such results may be important across S&E, as well as other domains such as finance and economics, where extremes are often of significant interest. Furthermore, to our knowledge, this is the first UQ model in SD where both aleatoric and epistemic uncertainties are characterized.

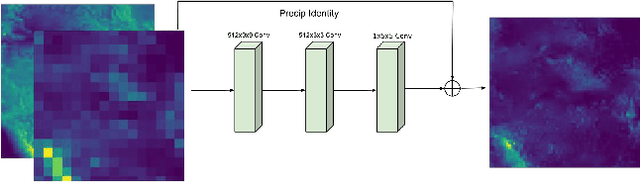
DeepSD: Generating High Resolution Climate Change Projections through Single Image Super-Resolution

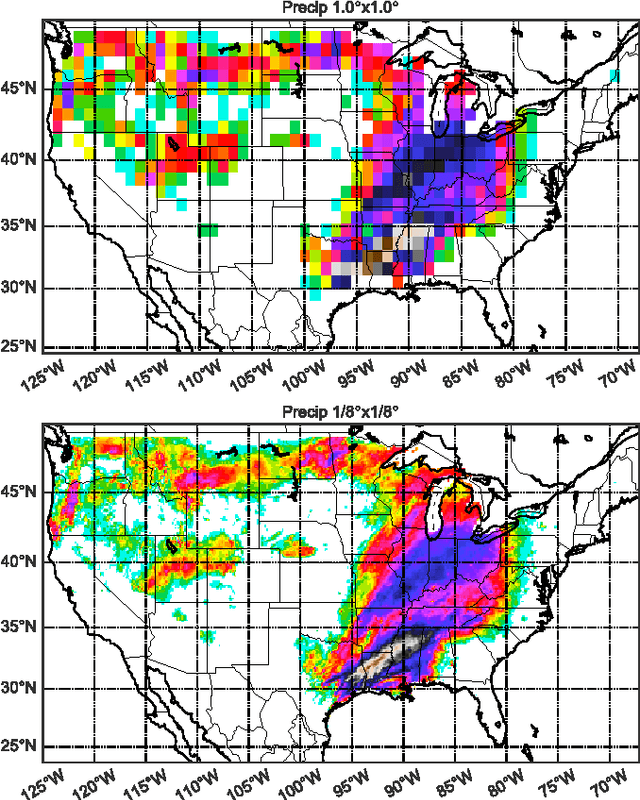
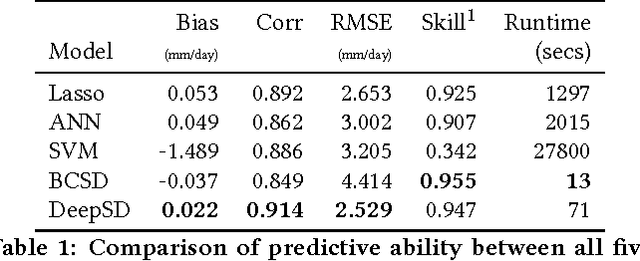
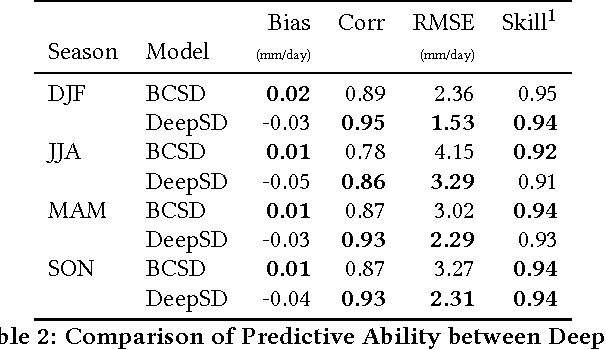
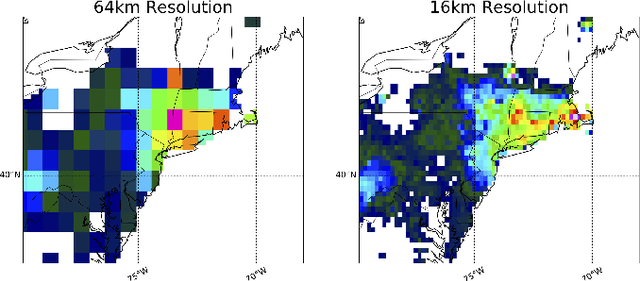
The impacts of climate change are felt by most critical systems, such as infrastructure, ecological systems, and power-plants. However, contemporary Earth System Models (ESM) are run at spatial resolutions too coarse for assessing effects this localized. Local scale projections can be obtained using statistical downscaling, a technique which uses historical climate observations to learn a low-resolution to high-resolution mapping. Depending on statistical modeling choices, downscaled projections have been shown to vary significantly terms of accuracy and reliability. The spatio-temporal nature of the climate system motivates the adaptation of super-resolution image processing techniques to statistical downscaling. In our work, we present DeepSD, a generalized stacked super resolution convolutional neural network (SRCNN) framework for statistical downscaling of climate variables. DeepSD augments SRCNN with multi-scale input channels to maximize predictability in statistical downscaling. We provide a comparison with Bias Correction Spatial Disaggregation as well as three Automated-Statistical Downscaling approaches in downscaling daily precipitation from 1 degree (~100km) to 1/8 degrees (~12.5km) over the Continental United States. Furthermore, a framework using the NASA Earth Exchange (NEX) platform is discussed for downscaling more than 20 ESM models with multiple emission scenarios.

Intercomparison of Machine Learning Methods for Statistical Downscaling: The Case of Daily and Extreme Precipitation

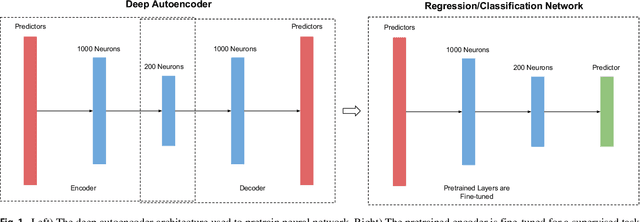
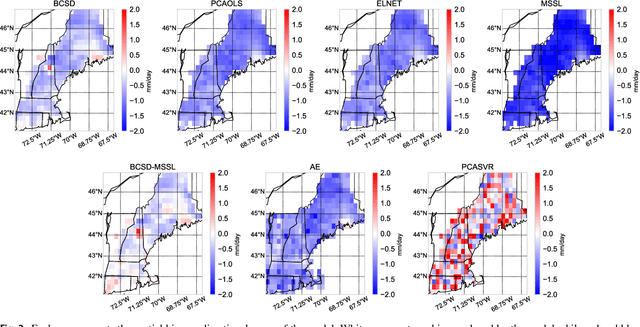
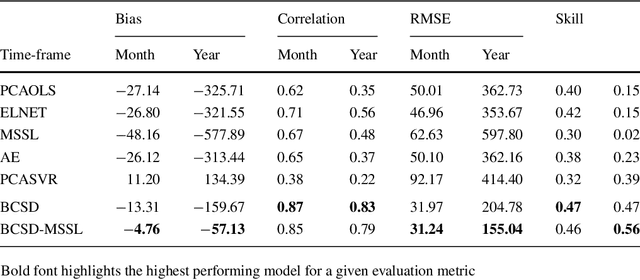
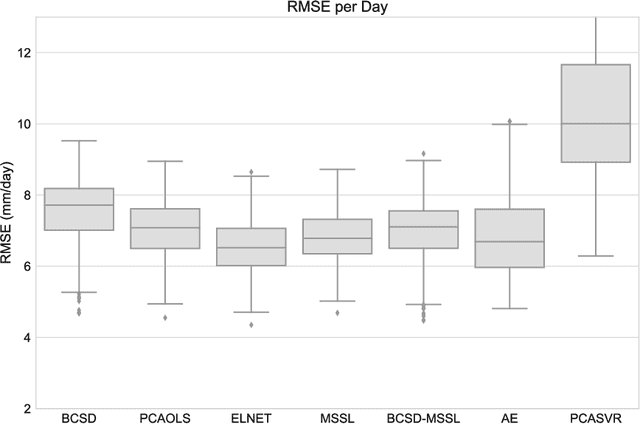
Statistical downscaling of global climate models (GCMs) allows researchers to study local climate change effects decades into the future. A wide range of statistical models have been applied to downscaling GCMs but recent advances in machine learning have not been explored. In this paper, we compare four fundamental statistical methods, Bias Correction Spatial Disaggregation (BCSD), Ordinary Least Squares, Elastic-Net, and Support Vector Machine, with three more advanced machine learning methods, Multi-task Sparse Structure Learning (MSSL), BCSD coupled with MSSL, and Convolutional Neural Networks to downscale daily precipitation in the Northeast United States. Metrics to evaluate of each method's ability to capture daily anomalies, large scale climate shifts, and extremes are analyzed. We find that linear methods, led by BCSD, consistently outperform non-linear approaches. The direct application of state-of-the-art machine learning methods to statistical downscaling does not provide improvements over simpler, longstanding approaches.