Bayesian Deep Learning Hyperparameter Search for Robust Function Mapping to Polynomials with Noise
Paper and Code
Jun 23, 2021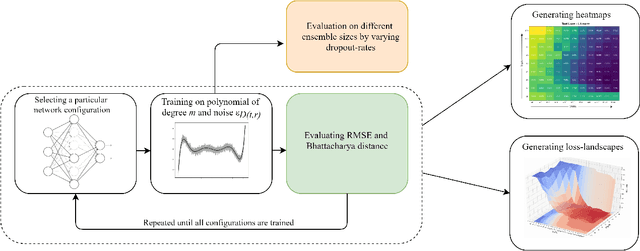
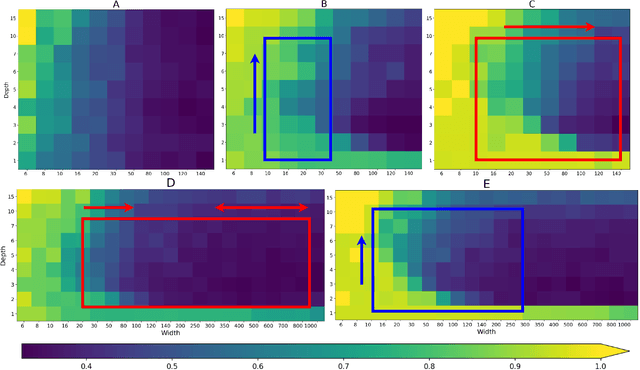
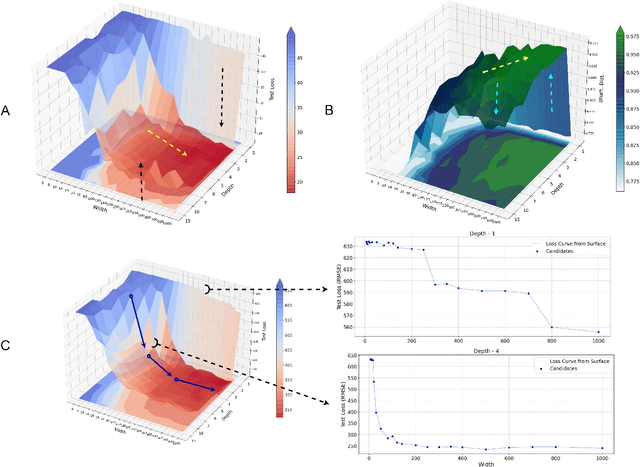
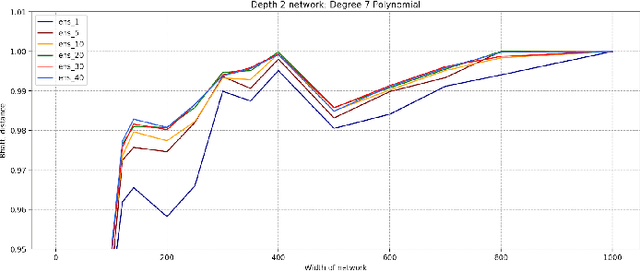
Advances in neural architecture search, as well as explainability and interpretability of connectionist architectures, have been reported in the recent literature. However, our understanding of how to design Bayesian Deep Learning (BDL) hyperparameters, specifically, the depth, width and ensemble size, for robust function mapping with uncertainty quantification, is still emerging. This paper attempts to further our understanding by mapping Bayesian connectionist representations to polynomials of different orders with varying noise types and ratios. We examine the noise-contaminated polynomials to search for the combination of hyperparameters that can extract the underlying polynomial signals while quantifying uncertainties based on the noise attributes. Specifically, we attempt to study the question that an appropriate neural architecture and ensemble configuration can be found to detect a signal of any n-th order polynomial contaminated with noise having different distributions and signal-to-noise (SNR) ratios and varying noise attributes. Our results suggest the possible existence of an optimal network depth as well as an optimal number of ensembles for prediction skills and uncertainty quantification, respectively. However, optimality is not discernible for width, even though the performance gain reduces with increasing width at high values of width. Our experiments and insights can be directional to understand theoretical properties of BDL representations and to design practical solutions.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge