Generalization Bounds for Physics-Informed Neural Networks for the Incompressible Navier-Stokes Equations

This work establishes rigorous first-of-its-kind upper bounds on the generalization error for the method of approximating solutions to the (d+1)-dimensional incompressible Navier-Stokes equations by training depth-2 neural networks trained via the unsupervised Physics-Informed Neural Network (PINN) framework. This is achieved by bounding the Rademacher complexity of the PINN risk. For appropriately weight bounded net classes our derived generalization bounds do not explicitly depend on the network width and our framework characterizes the generalization gap in terms of the fluid's kinematic viscosity and loss regularization parameters. In particular, the resulting sample complexity bounds are dimension-independent. Our generalization bounds suggest using novel activation functions for solving fluid dynamics. We provide empirical validation of the suggested activation functions and the corresponding bounds on a PINN setup solving the Taylor-Green vortex benchmark.

Noisy PDE Training Requires Bigger PINNs

Physics-Informed Neural Networks (PINNs) are increasingly used to approximate solutions of partial differential equations (PDEs), especially in high dimensions. In real-world applications, data samples are noisy, so it is important to know when a predictor can still achieve low empirical risk. However, little is known about the conditions under which a PINN can do so effectively. We prove a lower bound on the size of neural networks required for the supervised PINN empirical risk to fall below the variance of noisy supervision labels. Specifically, if a predictor achieves an empirical risk $O(\eta)$ below $\sigma^2$ (variance of supervision data), then necessarily $d_N\log d_N\gtrsim N_s \eta^2$, where $N_s$ is the number of samples and $d_N$ is the number of trainable parameters of the PINN. A similar constraint applies to the fully unsupervised PINN setting when boundary labels are sampled noisily. Consequently, increasing the number of noisy supervision labels alone does not provide a ``free lunch'' in reducing empirical risk. We also show empirically that PINNs can indeed achieve empirical risks below $\sigma^2$ under such conditions. As a case study, we investigate PINNs applied to the Hamilton--Jacobi--Bellman (HJB) PDE. Our findings lay the groundwork for quantitatively understanding the parameter requirements for training PINNs in the presence of noise.

Langevin Monte-Carlo Provably Learns Depth Two Neural Nets at Any Size and Data

In this work, we will establish that the Langevin Monte-Carlo algorithm can learn depth-2 neural nets of any size and for any data and we give non-asymptotic convergence rates for it. We achieve this via showing that under Total Variation distance and q-Renyi divergence, the iterates of Langevin Monte Carlo converge to the Gibbs distribution of Frobenius norm regularized losses for any of these nets, when using smooth activations and in both classification and regression settings. Most critically, the amount of regularization needed for our results is independent of the size of the net. The key observation of ours is that two layer neural loss functions can always be regularized by a constant amount such that they satisfy the Villani conditions, and thus their Gibbs measures satisfy a Poincare inequality.

Improving PINNs By Algebraic Inclusion of Boundary and Initial Conditions

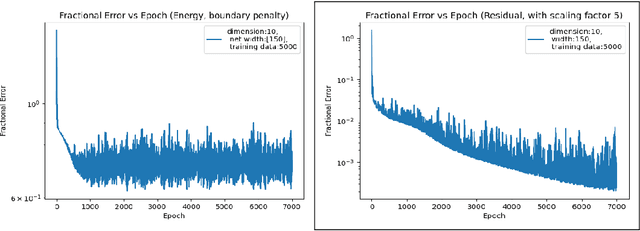
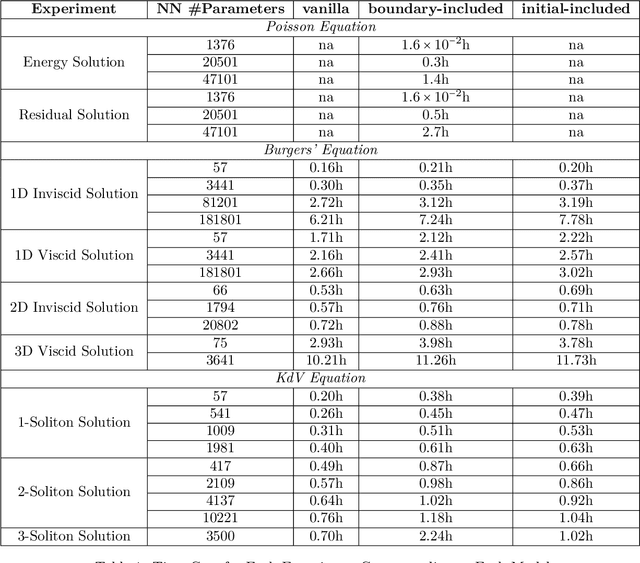
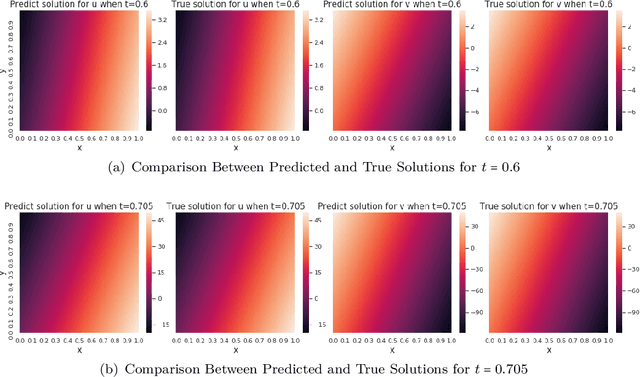
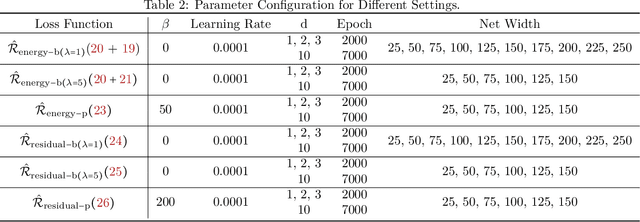
"AI for Science" aims to solve fundamental scientific problems using AI techniques. As most physical phenomena can be described as Partial Differential Equations (PDEs) , approximating their solutions using neural networks has evolved as a central component of scientific-ML. Physics-Informed Neural Networks (PINNs) is the general method that has evolved for this task but its training is well-known to be very unstable. In this work we explore the possibility of changing the model being trained from being just a neural network to being a non-linear transformation of it - one that algebraically includes the boundary/initial conditions. This reduces the number of terms in the loss function than the standard PINN losses. We demonstrate that our modification leads to significant performance gains across a range of benchmark tasks, in various dimensions and without having to tweak the training algorithm. Our conclusions are based on conducting hundreds of experiments, in the fully unsupervised setting, over multiple linear and non-linear PDEs set to exactly solvable scenarios, which lends to a concrete measurement of our performance gains in terms of order(s) of magnitude lower fractional errors being achieved, than by standard PINNs. The code accompanying this manuscript is publicly available at, https://github.com/MorganREN/Improving-PINNs-By-Algebraic-Inclusion-of-Boundary-and-Initial-Conditions

Regularized Gradient Clipping Provably Trains Wide and Deep Neural Networks

In this work, we instantiate a regularized form of the gradient clipping algorithm and prove that it can converge to the global minima of deep neural network loss functions provided that the net is of sufficient width. We present empirical evidence that our theoretically founded regularized gradient clipping algorithm is also competitive with the state-of-the-art deep-learning heuristics. Hence the algorithm presented here constitutes a new approach to rigorous deep learning. The modification we do to standard gradient clipping is designed to leverage the PL* condition, a variant of the Polyak-Lojasiewicz inequality which was recently proven to be true for various neural networks for any depth within a neighborhood of the initialisation.

Investigating the Ability of PINNs To Solve Burgers' PDE Near Finite-Time BlowUp

Physics Informed Neural Networks (PINNs) have been achieving ever newer feats of solving complicated PDEs numerically while offering an attractive trade-off between accuracy and speed of inference. A particularly challenging aspect of PDEs is that there exist simple PDEs which can evolve into singular solutions in finite time starting from smooth initial conditions. In recent times some striking experiments have suggested that PINNs might be good at even detecting such finite-time blow-ups. In this work, we embark on a program to investigate this stability of PINNs from a rigorous theoretical viewpoint. Firstly, we derive generalization bounds for PINNs for Burgers' PDE, in arbitrary dimensions, under conditions that allow for a finite-time blow-up. Then we demonstrate via experiments that our bounds are significantly correlated to the $\ell_2$-distance of the neurally found surrogate from the true blow-up solution, when computed on sequences of PDEs that are getting increasingly close to a blow-up.

LIPEx -- Locally Interpretable Probabilistic Explanations -- To Look Beyond The True Class

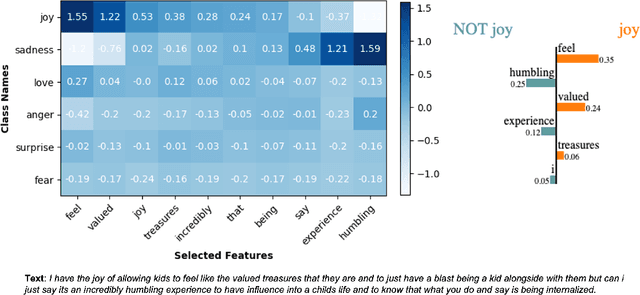
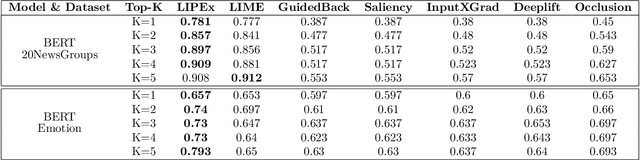
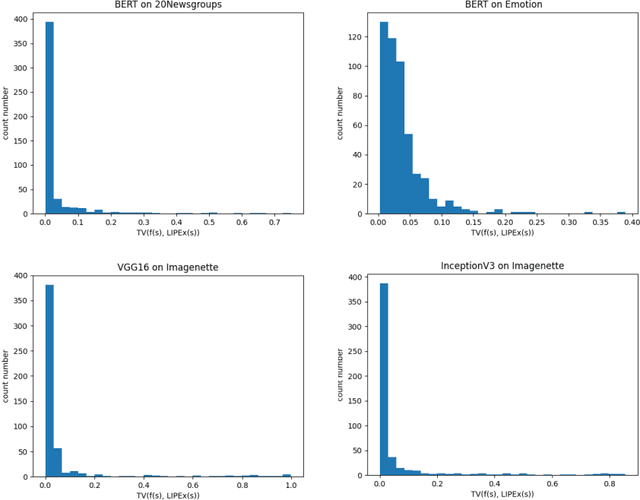
In this work, we instantiate a novel perturbation-based multi-class explanation framework, LIPEx (Locally Interpretable Probabilistic Explanation). We demonstrate that LIPEx not only locally replicates the probability distributions output by the widely used complex classification models but also provides insight into how every feature deemed to be important affects the prediction probability for each of the possible classes. We achieve this by defining the explanation as a matrix obtained via regression with respect to the Hellinger distance in the space of probability distributions. Ablation tests on text and image data, show that LIPEx-guided removal of important features from the data causes more change in predictions for the underlying model than similar tests on other saliency-based or feature importance-based XAI methods. It is also shown that compared to LIME, LIPEx is much more data efficient in terms of the number of perturbations needed for reliable evaluation of the explanation.

Global Convergence of SGD For Logistic Loss on Two Layer Neural Nets

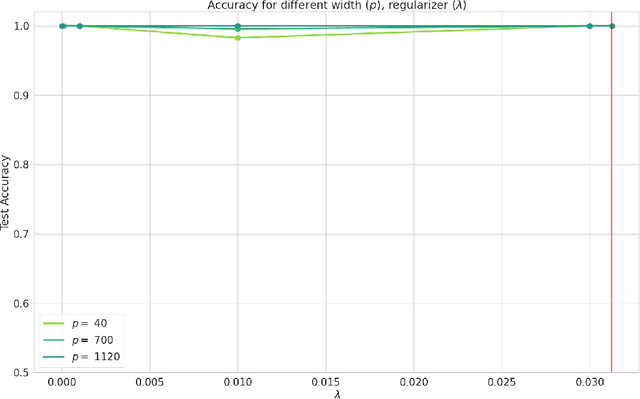
In this note, we demonstrate a first-of-its-kind provable convergence of SGD to the global minima of appropriately regularized logistic empirical risk of depth $2$ nets -- for arbitrary data and with any number of gates with adequately smooth and bounded activations like sigmoid and tanh. We also prove an exponentially fast convergence rate for continuous time SGD that also applies to smooth unbounded activations like SoftPlus. Our key idea is to show the existence of Frobenius norm regularized logistic loss functions on constant-sized neural nets which are "Villani functions" and thus be able to build on recent progress with analyzing SGD on such objectives.

Size Lowerbounds for Deep Operator Networks

Deep Operator Networks are an increasingly popular paradigm for solving regression in infinite dimensions and hence solve families of PDEs in one shot. In this work, we aim to establish a first-of-its-kind data-dependent lowerbound on the size of DeepONets required for them to be able to reduce empirical error on noisy data. In particular, we show that for low training errors to be obtained on $n$ data points it is necessary that the common output dimension of the branch and the trunk net be scaling as $\Omega \left ( {\sqrt{n}} \right )$. This inspires our experiments with DeepONets solving the advection-diffusion-reaction PDE, where we demonstrate the possibility that at a fixed model size, to leverage increase in this common output dimension and get monotonic lowering of training error, the size of the training data might necessarily need to scale quadratically with it.

Global Convergence of SGD On Two Layer Neural Nets

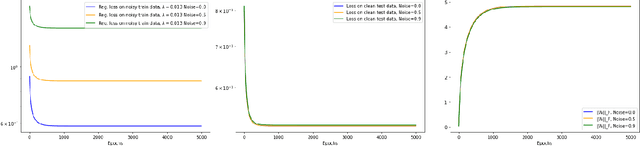
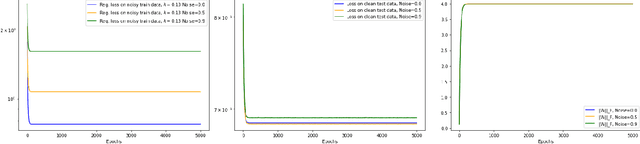
In this note we demonstrate provable convergence of SGD to the global minima of appropriately regularized $\ell_2-$empirical risk of depth $2$ nets -- for arbitrary data and with any number of gates, if they are using adequately smooth and bounded activations like sigmoid and tanh. We build on the results in [1] and leverage a constant amount of Frobenius norm regularization on the weights, along with sampling of the initial weights from an appropriate distribution. We also give a continuous time SGD convergence result that also applies to smooth unbounded activations like SoftPlus. Our key idea is to show the existence loss functions on constant sized neural nets which are "Villani Functions". [1] Bin Shi, Weijie J. Su, and Michael I. Jordan. On learning rates and schr\"odinger operators, 2020. arXiv:2004.06977