Global Convergence of SGD On Two Layer Neural Nets
Paper and Code
Oct 20, 2022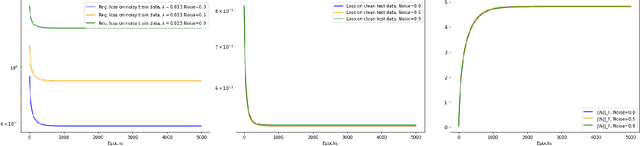
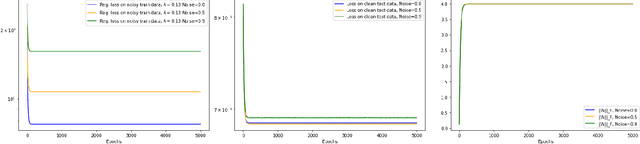


In this note we demonstrate provable convergence of SGD to the global minima of appropriately regularized $\ell_2-$empirical risk of depth $2$ nets -- for arbitrary data and with any number of gates, if they are using adequately smooth and bounded activations like sigmoid and tanh. We build on the results in [1] and leverage a constant amount of Frobenius norm regularization on the weights, along with sampling of the initial weights from an appropriate distribution. We also give a continuous time SGD convergence result that also applies to smooth unbounded activations like SoftPlus. Our key idea is to show the existence loss functions on constant sized neural nets which are "Villani Functions". [1] Bin Shi, Weijie J. Su, and Michael I. Jordan. On learning rates and schr\"odinger operators, 2020. arXiv:2004.06977
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge