PFedDST: Personalized Federated Learning with Decentralized Selection Training

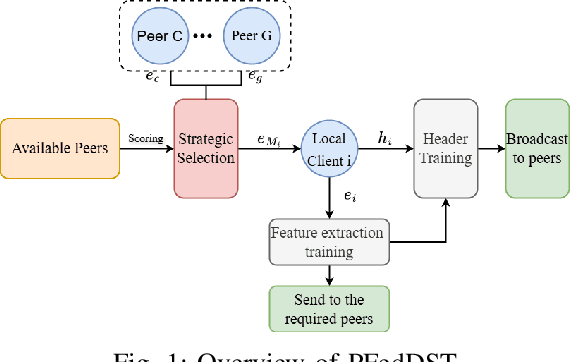
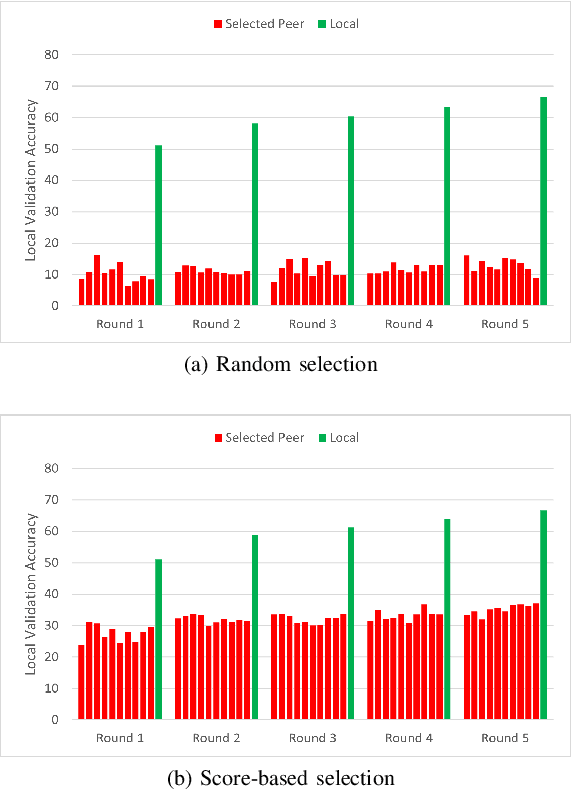
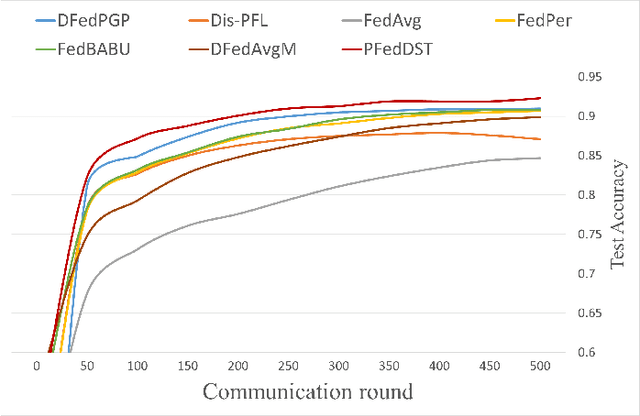
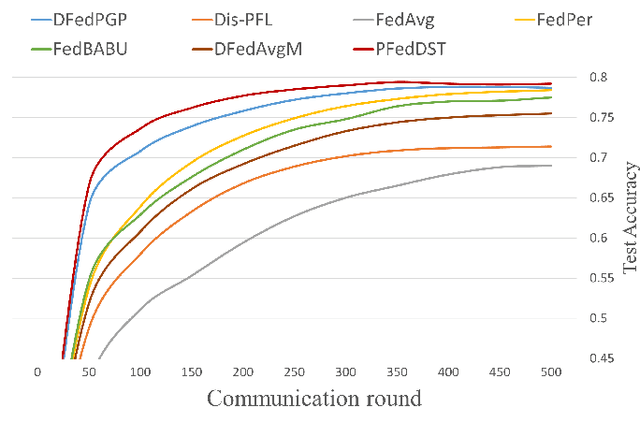
Distributed Learning (DL) enables the training of machine learning models across multiple devices, yet it faces challenges like non-IID data distributions and device capability disparities, which can impede training efficiency. Communication bottlenecks further complicate traditional Federated Learning (FL) setups. To mitigate these issues, we introduce the Personalized Federated Learning with Decentralized Selection Training (PFedDST) framework. PFedDST enhances model training by allowing devices to strategically evaluate and select peers based on a comprehensive communication score. This score integrates loss, task similarity, and selection frequency, ensuring optimal peer connections. This selection strategy is tailored to increase local personalization and promote beneficial peer collaborations to strengthen the stability and efficiency of the training process. Our experiments demonstrate that PFedDST not only enhances model accuracy but also accelerates convergence. This approach outperforms state-of-the-art methods in handling data heterogeneity, delivering both faster and more effective training in diverse and decentralized systems.

Measuring Heterogeneity in Machine Learning with Distributed Energy Distance

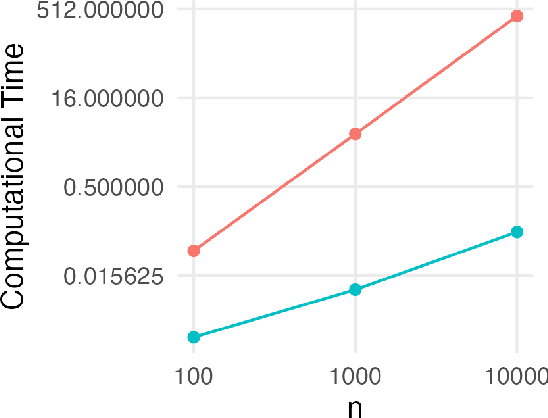
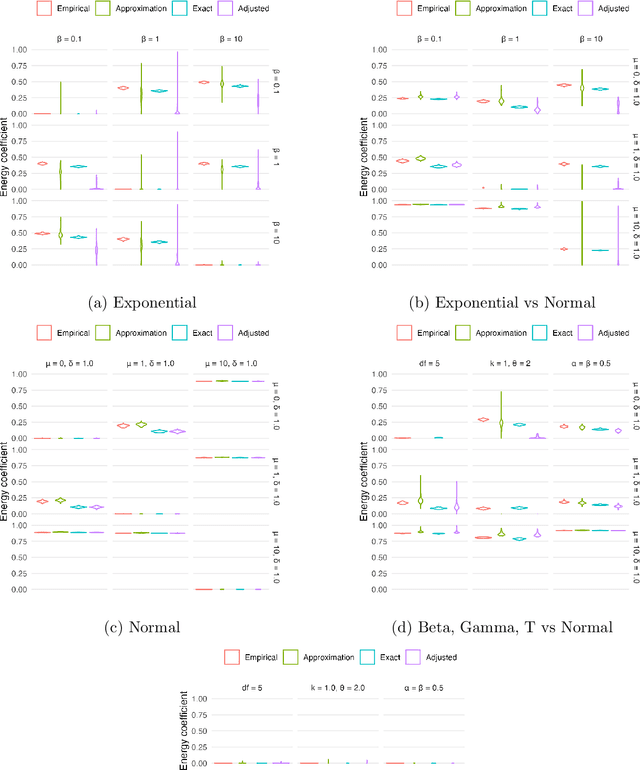
In distributed and federated learning, heterogeneity across data sources remains a major obstacle to effective model aggregation and convergence. We focus on feature heterogeneity and introduce energy distance as a sensitive measure for quantifying distributional discrepancies. While we show that energy distance is robust for detecting data distribution shifts, its direct use in large-scale systems can be prohibitively expensive. To address this, we develop Taylor approximations that preserve key theoretical quantitative properties while reducing computational overhead. Through simulation studies, we show how accurately capturing feature discrepancies boosts convergence in distributed learning. Finally, we propose a novel application of energy distance to assign penalty weights for aligning predictions across heterogeneous nodes, ultimately enhancing coordination in federated and distributed settings.

Impacts of Darwinian Evolution on Pre-trained Deep Neural Networks

Darwinian evolution of the biological brain is documented through multiple lines of evidence, although the modes of evolutionary changes remain unclear. Drawing inspiration from the evolved neural systems (e.g., visual cortex), deep learning models have demonstrated superior performance in visual tasks, among others. While the success of training deep neural networks has been relying on back-propagation (BP) and its variants to learn representations from data, BP does not incorporate the evolutionary processes that govern biological neural systems. This work proposes a neural network optimization framework based on evolutionary theory. Specifically, BP-trained deep neural networks for visual recognition tasks obtained from the ending epochs are considered the primordial ancestors (initial population). Subsequently, the population evolved with differential evolution. Extensive experiments are carried out to examine the relationships between Darwinian evolution and neural network optimization, including the correspondence between datasets, environment, models, and living species. The empirical results show that the proposed framework has positive impacts on the network, with reduced over-fitting and an order of magnitude lower time complexity compared to BP. Moreover, the experiments show that the proposed framework performs well on deep neural networks and big datasets.

Improving PINNs By Algebraic Inclusion of Boundary and Initial Conditions

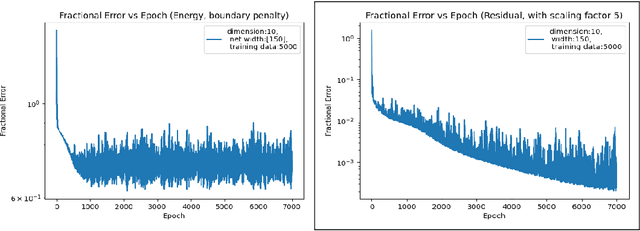
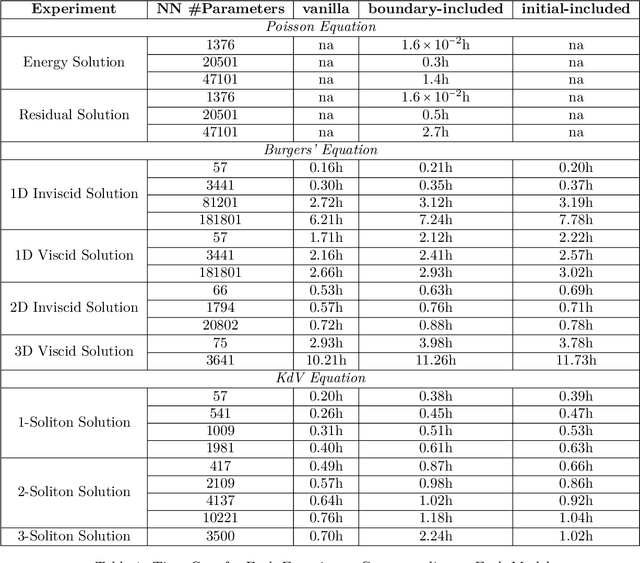
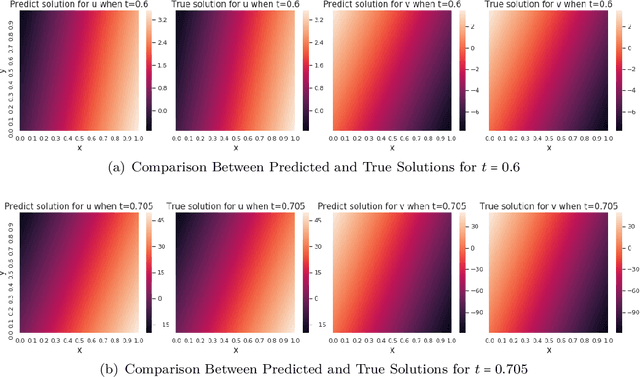
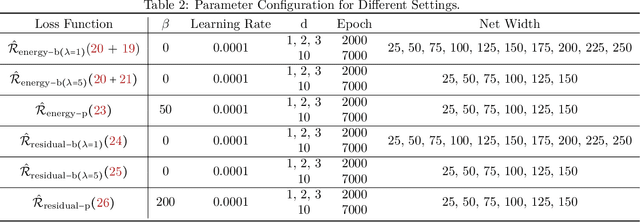
"AI for Science" aims to solve fundamental scientific problems using AI techniques. As most physical phenomena can be described as Partial Differential Equations (PDEs) , approximating their solutions using neural networks has evolved as a central component of scientific-ML. Physics-Informed Neural Networks (PINNs) is the general method that has evolved for this task but its training is well-known to be very unstable. In this work we explore the possibility of changing the model being trained from being just a neural network to being a non-linear transformation of it - one that algebraically includes the boundary/initial conditions. This reduces the number of terms in the loss function than the standard PINN losses. We demonstrate that our modification leads to significant performance gains across a range of benchmark tasks, in various dimensions and without having to tweak the training algorithm. Our conclusions are based on conducting hundreds of experiments, in the fully unsupervised setting, over multiple linear and non-linear PDEs set to exactly solvable scenarios, which lends to a concrete measurement of our performance gains in terms of order(s) of magnitude lower fractional errors being achieved, than by standard PINNs. The code accompanying this manuscript is publicly available at, https://github.com/MorganREN/Improving-PINNs-By-Algebraic-Inclusion-of-Boundary-and-Initial-Conditions

Interpretable Data Fusion for Distributed Learning: A Representative Approach via Gradient Matching

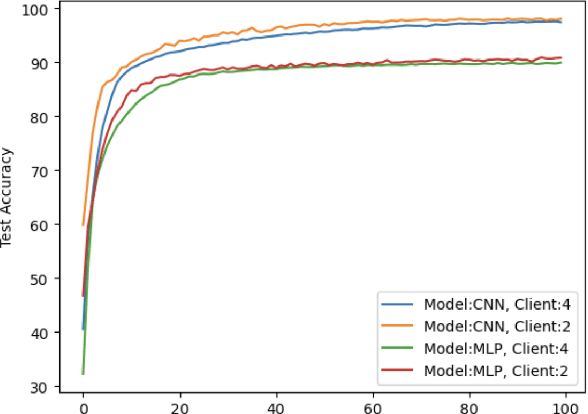
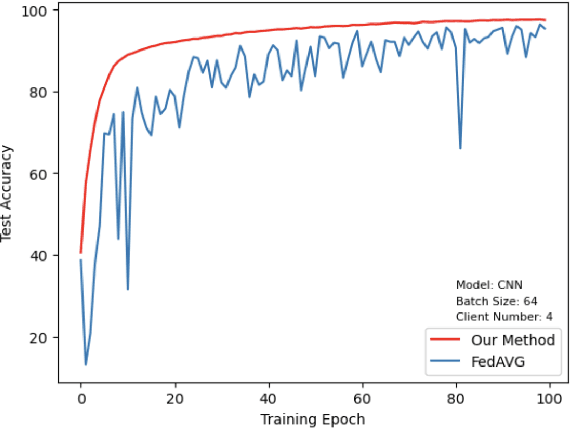
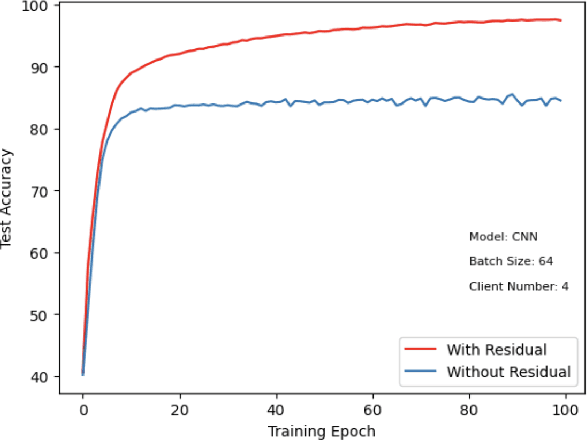
This paper introduces a representative-based approach for distributed learning that transforms multiple raw data points into a virtual representation. Unlike traditional distributed learning methods such as Federated Learning, which do not offer human interpretability, our method makes complex machine learning processes accessible and comprehensible. It achieves this by condensing extensive datasets into digestible formats, thus fostering intuitive human-machine interactions. Additionally, this approach maintains privacy and communication efficiency, and it matches the training performance of models using raw data. Simulation results show that our approach is competitive with or outperforms traditional Federated Learning in accuracy and convergence, especially in scenarios with complex models and a higher number of clients. This framework marks a step forward in integrating human intuition with machine intelligence, which potentially enhances human-machine learning interfaces and collaborative efforts.