An Empirical Study of the Occurrence of Heavy-Tails in Training a ReLU Gate

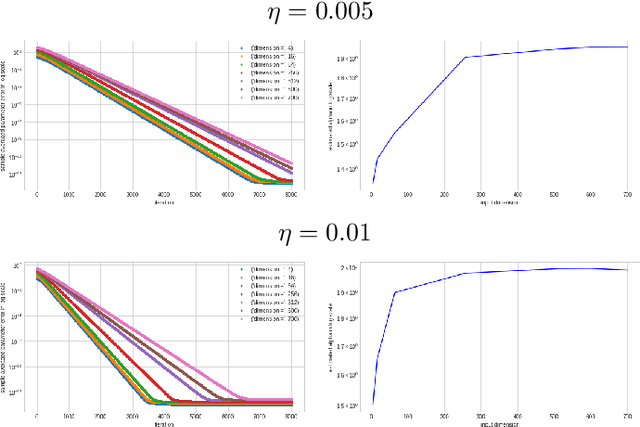
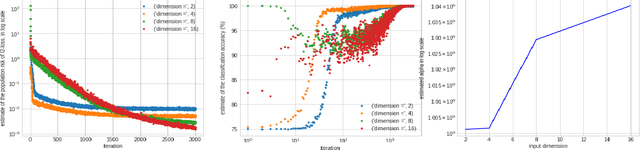
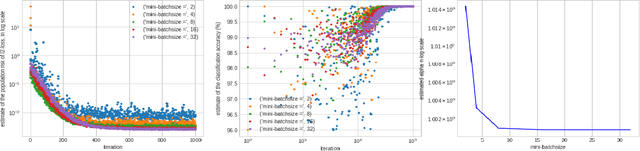
A particular direction of recent advance about stochastic deep-learning algorithms has been about uncovering a rather mysterious heavy-tailed nature of the stationary distribution of these algorithms, even when the data distribution is not so. Moreover, the heavy-tail index is known to show interesting dependence on the input dimension of the net, the mini-batch size and the step size of the algorithm. In this short note, we undertake an experimental study of this index for S.G.D. while training a $\relu$ gate (in the realizable and in the binary classification setup) and for a variant of S.G.D. that was proven in Karmakar and Mukherjee (2022) for ReLU realizable data. From our experiments we conjecture that these two algorithms have similar heavy-tail behaviour on any data where the latter can be proven to converge. Secondly, we demonstrate that the heavy-tail index of the late time iterates in this model scenario has strikingly different properties than either what has been proven for linear hypothesis classes or what has been previously demonstrated for large nets.