Sharp Gaussian approximations for Decentralized Federated Learning

Federated Learning has gained traction in privacy-sensitive collaborative environments, with local SGD emerging as a key optimization method in decentralized settings. While its convergence properties are well-studied, asymptotic statistical guarantees beyond convergence remain limited. In this paper, we present two generalized Gaussian approximation results for local SGD and explore their implications. First, we prove a Berry-Esseen theorem for the final local SGD iterates, enabling valid multiplier bootstrap procedures. Second, motivated by robustness considerations, we introduce two distinct time-uniform Gaussian approximations for the entire trajectory of local SGD. The time-uniform approximations support Gaussian bootstrap-based tests for detecting adversarial attacks. Extensive simulations are provided to support our theoretical results.

Capacity Bounds for the DeepONet Method of Solving Differential Equations

In recent times machine learning methods have made significant advances in becoming a useful tool for analyzing physical systems. A particularly active area in this theme has been "physics informed machine learning" [1] which focuses on using neural nets for numerically solving differential equations. Among all the proposals for solving differential equations using deep-learning, in this paper we aim to advance the theory of generalization error for DeepONets - which is unique among all the available ideas because of its particularly intriguing structure of having an inner-product of two neural nets. Our key contribution is to give a bound on the Rademacher complexity for a large class of DeepONets. Our bound does not explicitly scale with the number of parameters of the nets involved and is thus a step towards explaining the efficacy of overparameterized DeepONets. Additionally, a capacity bound such as ours suggests a novel regularizer on the neural net weights that can help in training DeepONets - irrespective of the differential equation being solved. [1] G. E. Karniadakis, I. G. Kevrekidis, L. Lu, P. Perdikaris, S. Wang, and L. Yang. Physics-informed machine learning. Nature Reviews Physics, 2021.

An Empirical Study of the Occurrence of Heavy-Tails in Training a ReLU Gate

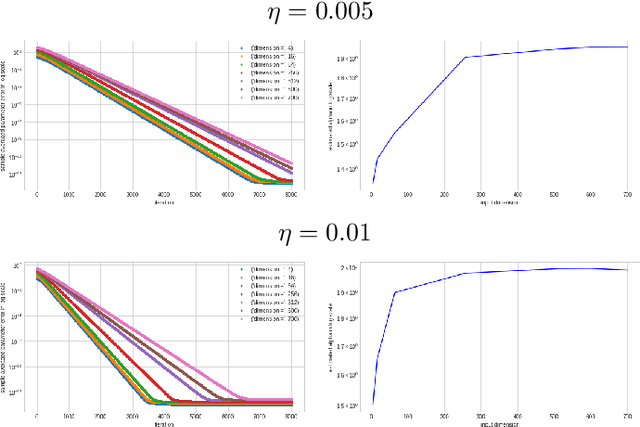
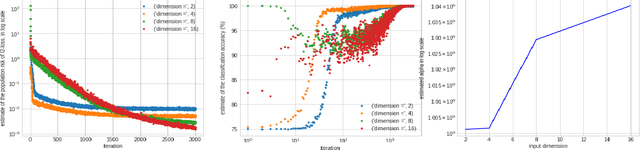
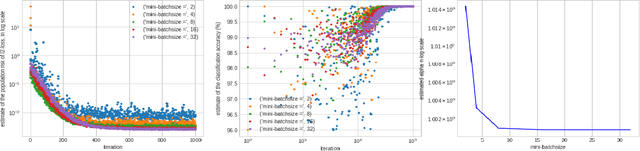
A particular direction of recent advance about stochastic deep-learning algorithms has been about uncovering a rather mysterious heavy-tailed nature of the stationary distribution of these algorithms, even when the data distribution is not so. Moreover, the heavy-tail index is known to show interesting dependence on the input dimension of the net, the mini-batch size and the step size of the algorithm. In this short note, we undertake an experimental study of this index for S.G.D. while training a $\relu$ gate (in the realizable and in the binary classification setup) and for a variant of S.G.D. that was proven in Karmakar and Mukherjee (2022) for ReLU realizable data. From our experiments we conjecture that these two algorithms have similar heavy-tail behaviour on any data where the latter can be proven to converge. Secondly, we demonstrate that the heavy-tail index of the late time iterates in this model scenario has strikingly different properties than either what has been proven for linear hypothesis classes or what has been previously demonstrated for large nets.