Amnon Catav
MultiModalQA: Complex Question Answering over Text, Tables and Images
Apr 13, 2021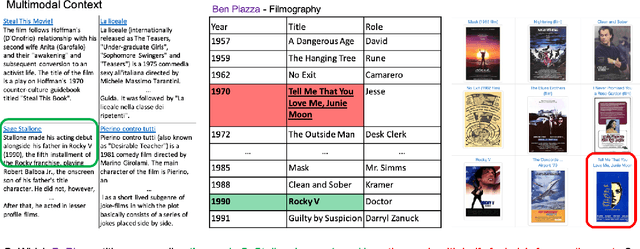
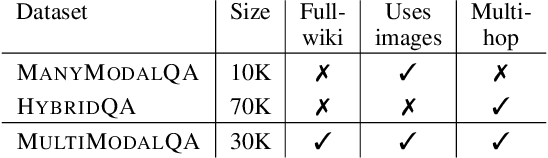

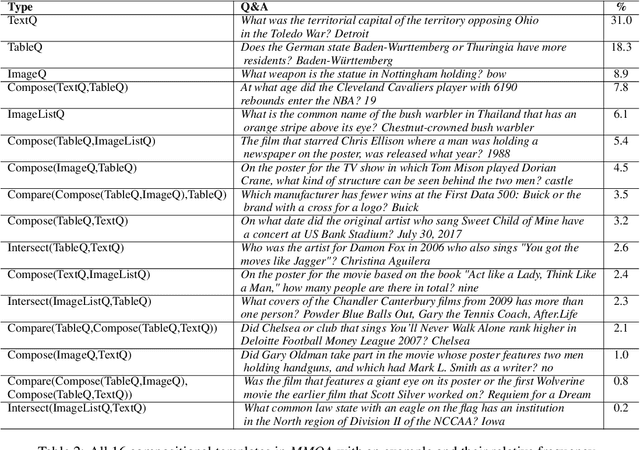
Abstract:When answering complex questions, people can seamlessly combine information from visual, textual and tabular sources. While interest in models that reason over multiple pieces of evidence has surged in recent years, there has been relatively little work on question answering models that reason across multiple modalities. In this paper, we present MultiModalQA(MMQA): a challenging question answering dataset that requires joint reasoning over text, tables and images. We create MMQA using a new framework for generating complex multi-modal questions at scale, harvesting tables from Wikipedia, and attaching images and text paragraphs using entities that appear in each table. We then define a formal language that allows us to take questions that can be answered from a single modality, and combine them to generate cross-modal questions. Last, crowdsourcing workers take these automatically-generated questions and rephrase them into more fluent language. We create 29,918 questions through this procedure, and empirically demonstrate the necessity of a multi-modal multi-hop approach to solve our task: our multi-hop model, ImplicitDecomp, achieves an average F1of 51.7 over cross-modal questions, substantially outperforming a strong baseline that achieves 38.2 F1, but still lags significantly behind human performance, which is at 90.1 F1
Marginal Contribution Feature Importance -- an Axiomatic Approach for The Natural Case
Oct 15, 2020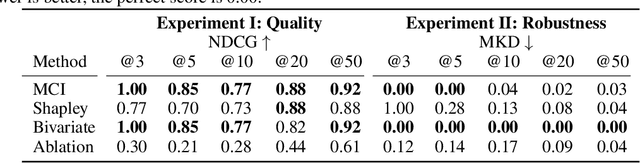
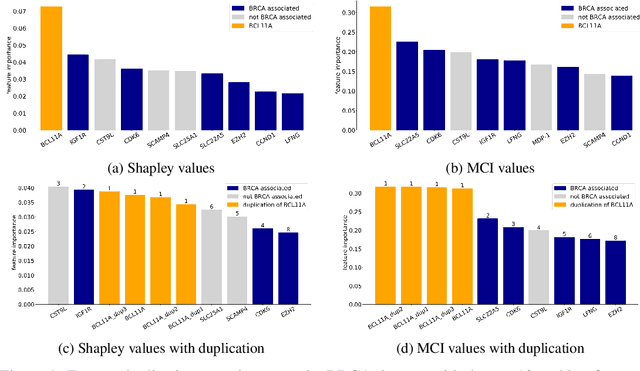
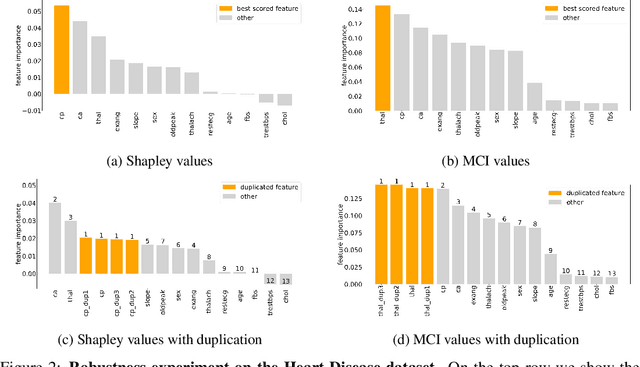
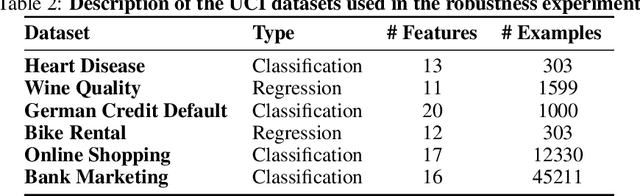
Abstract:When training a predictive model over medical data, the goal is sometimes to gain insights about a certain disease. In such cases, it is common to use feature importance as a tool to highlight significant factors contributing to that disease. As there are many existing methods for computing feature importance scores, understanding their relative merits is not trivial. Further, the diversity of scenarios in which they are used lead to different expectations from the feature importance scores. While it is common to make the distinction between local scores that focus on individual predictions and global scores that look at the contribution of a feature to the model, another important division distinguishes model scenarios, in which the goal is to understand predictions of a given model from natural scenarios, in which the goal is to understand a phenomenon such as a disease. We develop a set of axioms that represent the properties expected from a feature importance function in the natural scenario and prove that there exists only one function that satisfies all of them, the Marginal Contribution Feature Importance (MCI). We analyze this function for its theoretical and empirical properties and compare it to other feature importance scores. While our focus is the natural scenario, we suggest that our axiomatic approach could be carried out in other scenarios too.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge