Sriram Sankararaman
dotears: Scalable, consistent DAG estimation using observational and interventional data
May 30, 2023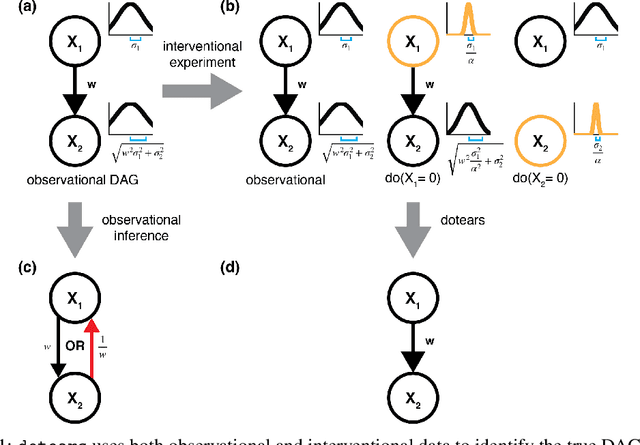

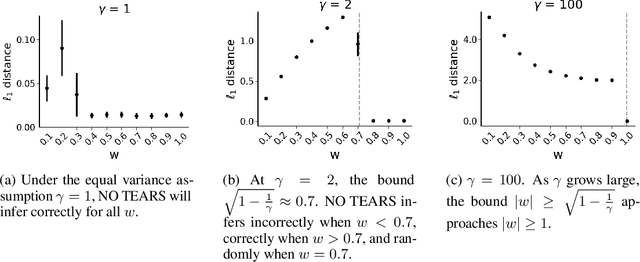
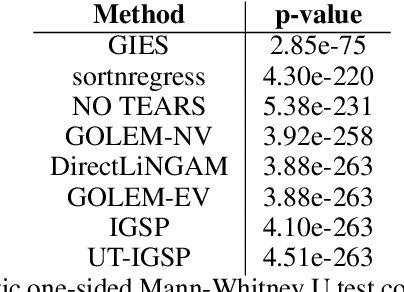
Abstract:Learning causal directed acyclic graphs (DAGs) from data is complicated by a lack of identifiability and the combinatorial space of solutions. Recent work has improved tractability of score-based structure learning of DAGs in observational data, but is sensitive to the structure of the exogenous error variances. On the other hand, learning exogenous variance structure from observational data requires prior knowledge of structure. Motivated by new biological technologies that link highly parallel gene interventions to a high-dimensional observation, we present $\texttt{dotears}$ [doo-tairs], a scalable structure learning framework which leverages observational and interventional data to infer a single causal structure through continuous optimization. $\texttt{dotears}$ exploits predictable structural consequences of interventions to directly estimate the exogenous error structure, bypassing the circular estimation problem. We extend previous work to show, both empirically and analytically, that the inferences of previous methods are driven by exogenous variance structure, but $\texttt{dotears}$ is robust to exogenous variance structure. Across varied simulations of large random DAGs, $\texttt{dotears}$ outperforms state-of-the-art methods in structure estimation. Finally, we show that $\texttt{dotears}$ is a provably consistent estimator of the true DAG under mild assumptions.
Contrastive Mixup: Self- and Semi-Supervised learning for Tabular Domain
Sep 01, 2021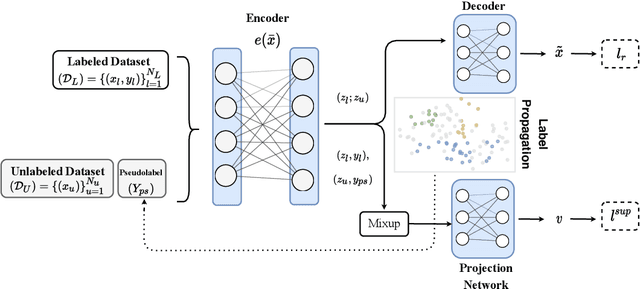
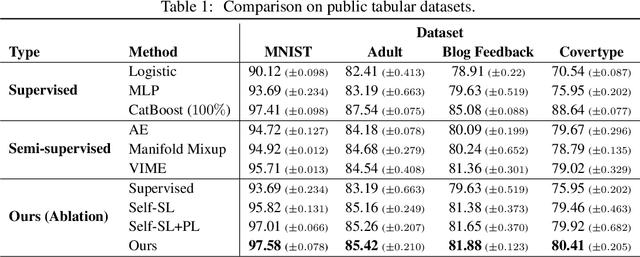
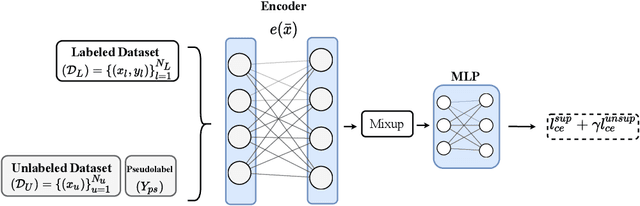
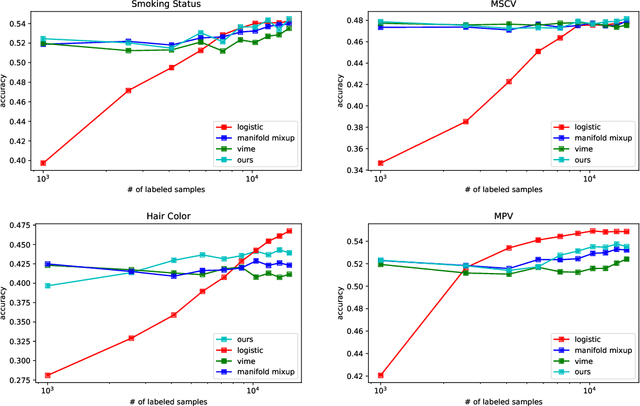
Abstract:Recent literature in self-supervised has demonstrated significant progress in closing the gap between supervised and unsupervised methods in the image and text domains. These methods rely on domain-specific augmentations that are not directly amenable to the tabular domain. Instead, we introduce Contrastive Mixup, a semi-supervised learning framework for tabular data and demonstrate its effectiveness in limited annotated data settings. Our proposed method leverages Mixup-based augmentation under the manifold assumption by mapping samples to a low dimensional latent space and encourage interpolated samples to have high a similarity within the same labeled class. Unlabeled samples are additionally employed via a transductive label propagation method to further enrich the set of similar and dissimilar pairs that can be used in the contrastive loss term. We demonstrate the effectiveness of the proposed framework on public tabular datasets and real-world clinical datasets.
Marginal Contribution Feature Importance -- an Axiomatic Approach for The Natural Case
Oct 15, 2020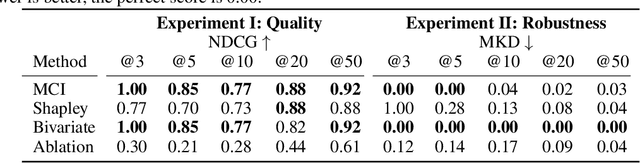
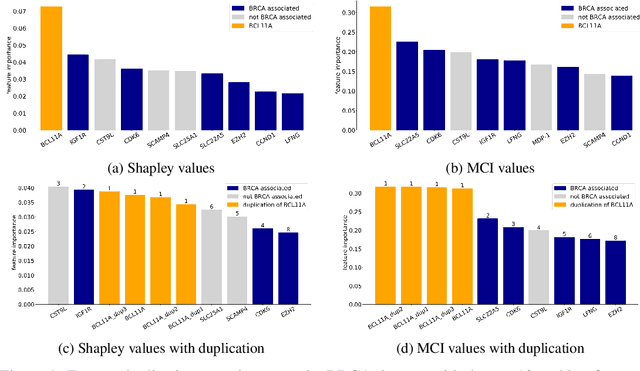
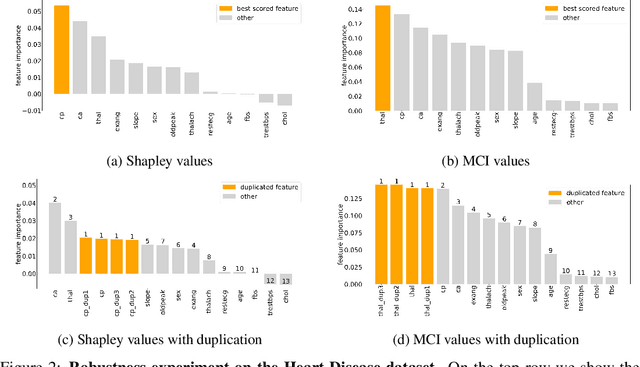
Abstract:When training a predictive model over medical data, the goal is sometimes to gain insights about a certain disease. In such cases, it is common to use feature importance as a tool to highlight significant factors contributing to that disease. As there are many existing methods for computing feature importance scores, understanding their relative merits is not trivial. Further, the diversity of scenarios in which they are used lead to different expectations from the feature importance scores. While it is common to make the distinction between local scores that focus on individual predictions and global scores that look at the contribution of a feature to the model, another important division distinguishes model scenarios, in which the goal is to understand predictions of a given model from natural scenarios, in which the goal is to understand a phenomenon such as a disease. We develop a set of axioms that represent the properties expected from a feature importance function in the natural scenario and prove that there exists only one function that satisfies all of them, the Marginal Contribution Feature Importance (MCI). We analyze this function for its theoretical and empirical properties and compare it to other feature importance scores. While our focus is the natural scenario, we suggest that our axiomatic approach could be carried out in other scenarios too.
Explaining Groups of Points in Low-Dimensional Representations
Mar 18, 2020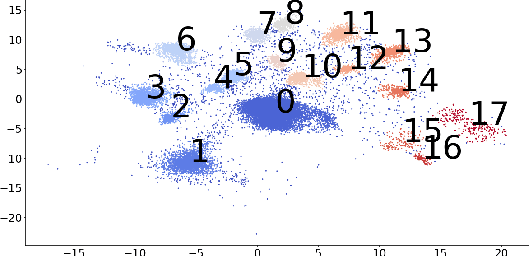
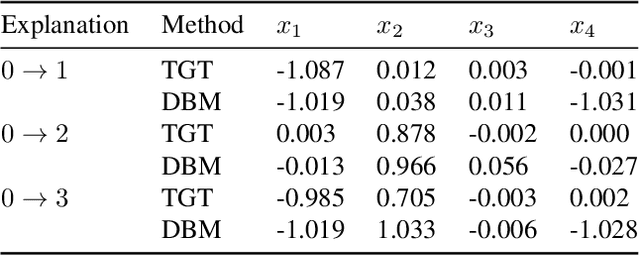
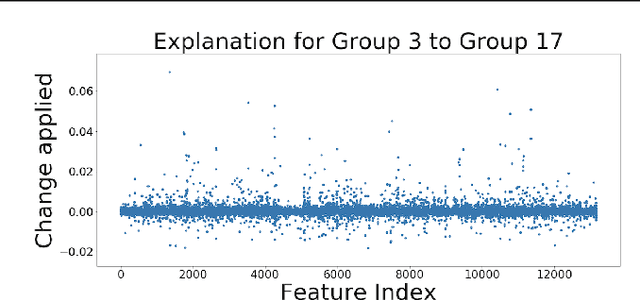
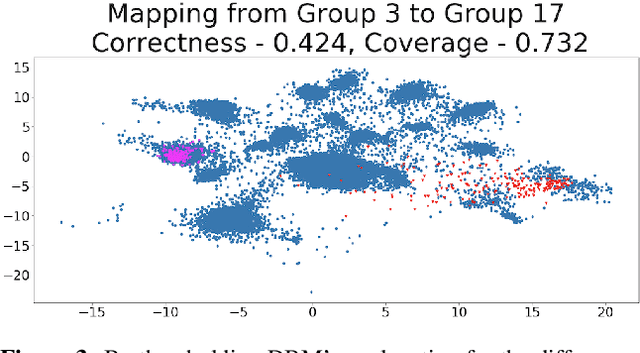
Abstract:A common workflow in data exploration is to learn a low-dimensional representation of the data, identify groups of points in that representation, and examine the differences between the groups to determine what they represent. We treat this as an interpretable machine learning problem by leveraging the model that learned the low-dimensional representation to help identify the key differences between the groups. To solve this problem, we introduce a new type of explanation, a Global Counterfactual Explanation (GCE), and our algorithm, Transitive Global Translations (TGT), for computing GCEs. TGT identifies the differences between each pair of groups using compressed sensing but constrains those pairwise differences to be consistent among all of the groups. Empirically, we demonstrate that TGT is able to identify explanations that accurately explain the model while being relatively sparse, and that these explanations match real patterns in the data.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge