The Gray Area: Characterizing Moderator Disagreement on Reddit

Volunteer moderators play a crucial role in sustaining online dialogue, but they often disagree about what should or should not be allowed. In this paper, we study the complexity of content moderation with a focus on disagreements between moderators, which we term the ``gray area'' of moderation. Leveraging 5 years and 4.3 million moderation log entries from 24 subreddits of different topics and sizes, we characterize how gray area, or disputed cases, differ from undisputed cases. We show that one-in-seven moderation cases are disputed among moderators, often addressing transgressions where users' intent is not directly legible, such as in trolling and brigading, as well as tensions around community governance. This is concerning, as almost half of all gray area cases involved automated moderation decisions. Through information-theoretic evaluations, we demonstrate that gray area cases are inherently harder to adjudicate than undisputed cases and show that state-of-the-art language models struggle to adjudicate them. We highlight the key role of expert human moderators in overseeing the moderation process and provide insights about the challenges of current moderation processes and tools.

LORE: Lagrangian-Optimized Robust Embeddings for Visual Encoders

Visual encoders have become fundamental components in modern computer vision pipelines. However, ensuring robustness against adversarial perturbations remains a critical challenge. Recent efforts have explored both supervised and unsupervised adversarial fine-tuning strategies. We identify two key limitations in these approaches: (i) they often suffer from instability, especially during the early stages of fine-tuning, resulting in suboptimal convergence and degraded performance on clean data, and (ii) they exhibit a suboptimal trade-off between robustness and clean data accuracy, hindering the simultaneous optimization of both objectives. To overcome these challenges, we propose Lagrangian-Optimized Robust Embeddings (LORE), a novel unsupervised adversarial fine-tuning framework. LORE utilizes constrained optimization, which offers a principled approach to balancing competing goals, such as improving robustness while preserving nominal performance. By enforcing embedding-space proximity constraints, LORE effectively maintains clean data performance throughout adversarial fine-tuning. Extensive experiments show that LORE significantly improves zero-shot adversarial robustness with minimal degradation in clean data accuracy. Furthermore, we demonstrate the effectiveness of the adversarially fine-tuned CLIP image encoder in out-of-distribution generalization and enhancing the interpretability of image embeddings.

One Goal, Many Challenges: Robust Preference Optimization Amid Content-Aware and Multi-Source Noise

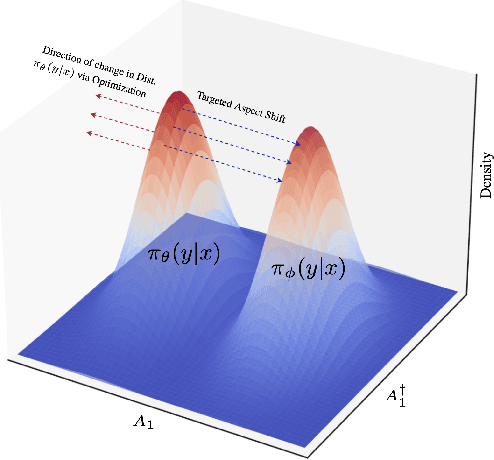
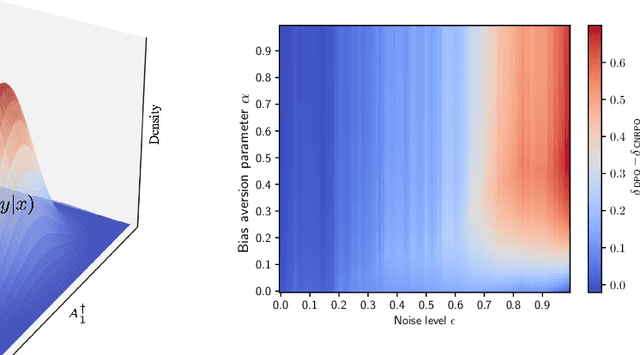
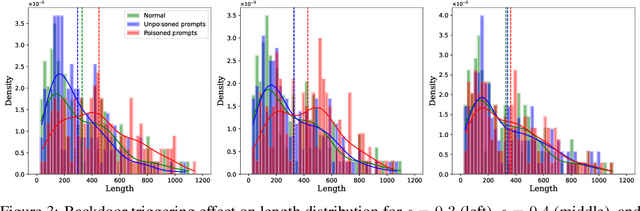
Large Language Models (LLMs) have made significant strides in generating human-like responses, largely due to preference alignment techniques. However, these methods often assume unbiased human feedback, which is rarely the case in real-world scenarios. This paper introduces Content-Aware Noise-Resilient Preference Optimization (CNRPO), a novel framework that addresses multiple sources of content-dependent noise in preference learning. CNRPO employs a multi-objective optimization approach to separate true preferences from content-aware noises, effectively mitigating their impact. We leverage backdoor attack mechanisms to efficiently learn and control various noise sources within a single model. Theoretical analysis and extensive experiments on different synthetic noisy datasets demonstrate that CNRPO significantly improves alignment with primary human preferences while controlling for secondary noises and biases, such as response length and harmfulness.

Cooperative Multi-Agent Constrained Stochastic Linear Bandits

In this study, we explore a collaborative multi-agent stochastic linear bandit setting involving a network of $N$ agents that communicate locally to minimize their collective regret while keeping their expected cost under a specified threshold $\tau$. Each agent encounters a distinct linear bandit problem characterized by its own reward and cost parameters, i.e., local parameters. The goal of the agents is to determine the best overall action corresponding to the average of these parameters, or so-called global parameters. In each round, an agent is randomly chosen to select an action based on its current knowledge of the system. This chosen action is then executed by all agents, then they observe their individual rewards and costs. We propose a safe distributed upper confidence bound algorithm, so called \textit{MA-OPLB}, and establish a high probability bound on its $T$-round regret. MA-OPLB utilizes an accelerated consensus method, where agents can compute an estimate of the average rewards and costs across the network by communicating the proper information with their neighbors. We show that our regret bound is of order $ \mathcal{O}\left(\frac{d}{\tau-c_0}\frac{\log(NT)^2}{\sqrt{N}}\sqrt{\frac{T}{\log(1/|\lambda_2|)}}\right)$, where $\lambda_2$ is the second largest (in absolute value) eigenvalue of the communication matrix, and $\tau-c_0$ is the known cost gap of a feasible action. We also experimentally show the performance of our proposed algorithm in different network structures.

Generalizable Spacecraft Trajectory Generation via Multimodal Learning with Transformers

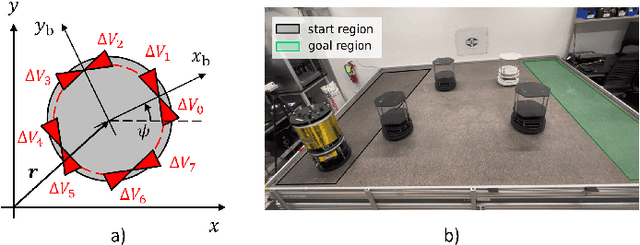
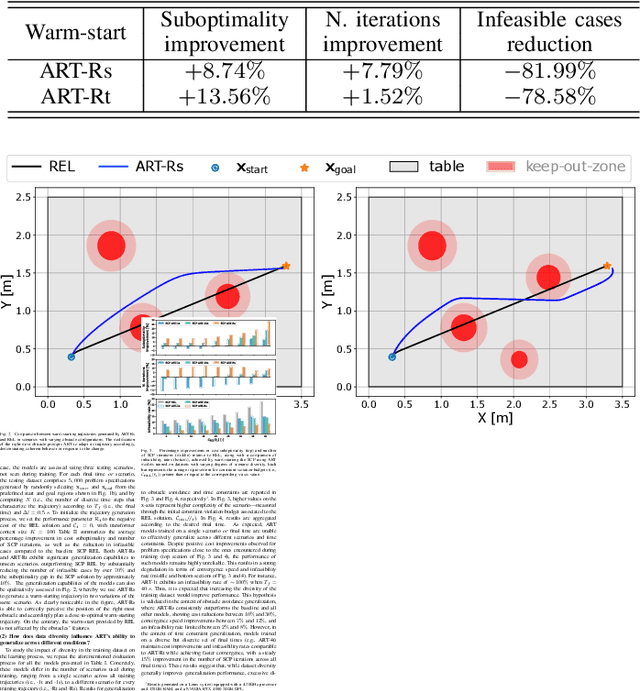
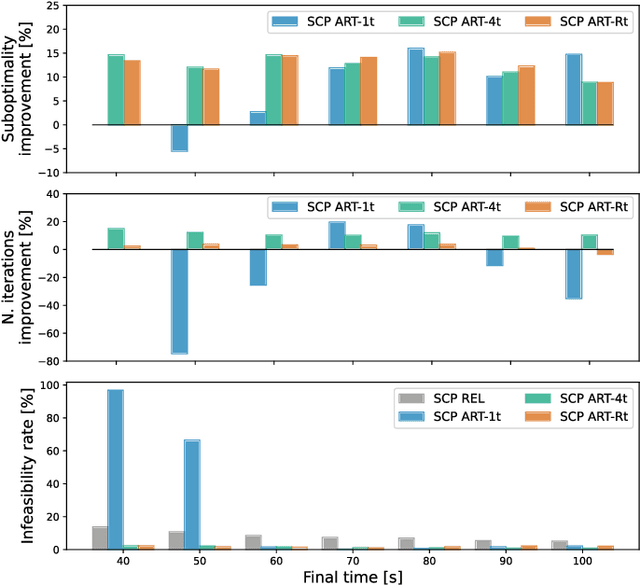
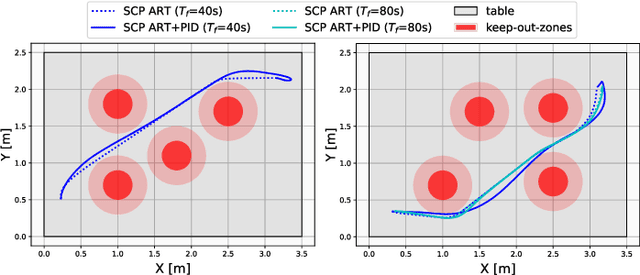
Effective trajectory generation is essential for reliable on-board spacecraft autonomy. Among other approaches, learning-based warm-starting represents an appealing paradigm for solving the trajectory generation problem, effectively combining the benefits of optimization- and data-driven methods. Current approaches for learning-based trajectory generation often focus on fixed, single-scenario environments, where key scene characteristics, such as obstacle positions or final-time requirements, remain constant across problem instances. However, practical trajectory generation requires the scenario to be frequently reconfigured, making the single-scenario approach a potentially impractical solution. To address this challenge, we present a novel trajectory generation framework that generalizes across diverse problem configurations, by leveraging high-capacity transformer neural networks capable of learning from multimodal data sources. Specifically, our approach integrates transformer-based neural network models into the trajectory optimization process, encoding both scene-level information (e.g., obstacle locations, initial and goal states) and trajectory-level constraints (e.g., time bounds, fuel consumption targets) via multimodal representations. The transformer network then generates near-optimal initial guesses for non-convex optimization problems, significantly enhancing convergence speed and performance. The framework is validated through extensive simulations and real-world experiments on a free-flyer platform, achieving up to 30% cost improvement and 80% reduction in infeasible cases with respect to traditional approaches, and demonstrating robust generalization across diverse scenario variations.

Markov Decision Processes with Noisy State Observation

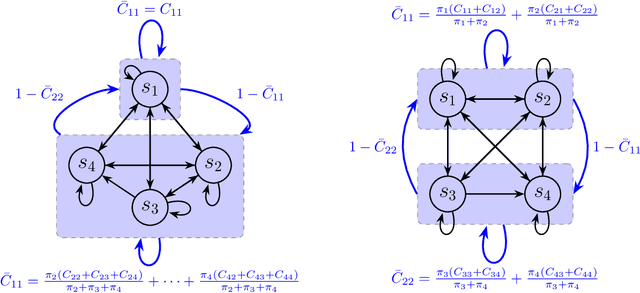
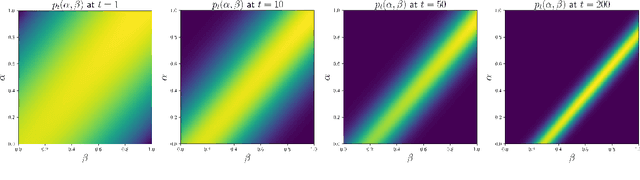
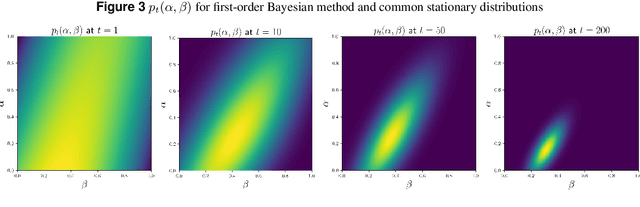
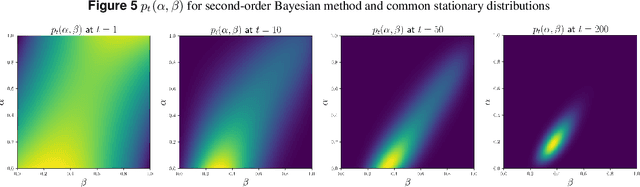
This paper addresses the challenge of a particular class of noisy state observations in Markov Decision Processes (MDPs), a common issue in various real-world applications. We focus on modeling this uncertainty through a confusion matrix that captures the probabilities of misidentifying the true state. Our primary goal is to estimate the inherent measurement noise, and to this end, we propose two novel algorithmic approaches. The first, the method of second-order repetitive actions, is designed for efficient noise estimation within a finite time window, providing identifiable conditions for system analysis. The second approach comprises a family of Bayesian algorithms, which we thoroughly analyze and compare in terms of performance and limitations. We substantiate our theoretical findings with simulations, demonstrating the effectiveness of our methods in different scenarios, particularly highlighting their behavior in environments with varying stationary distributions. Our work advances the understanding of reinforcement learning in noisy environments, offering robust techniques for more accurate state estimation in MDPs.

Convex Methods for Constrained Linear Bandits

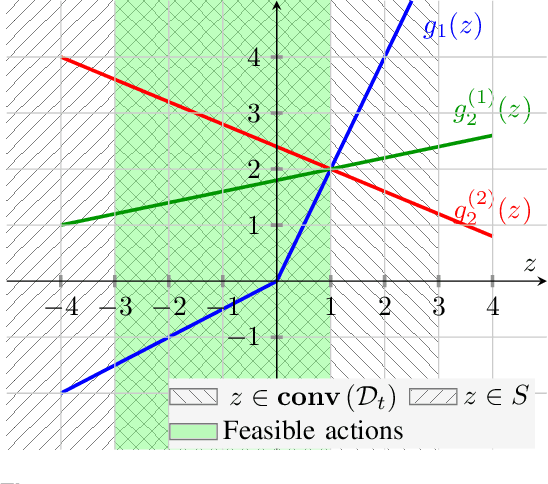
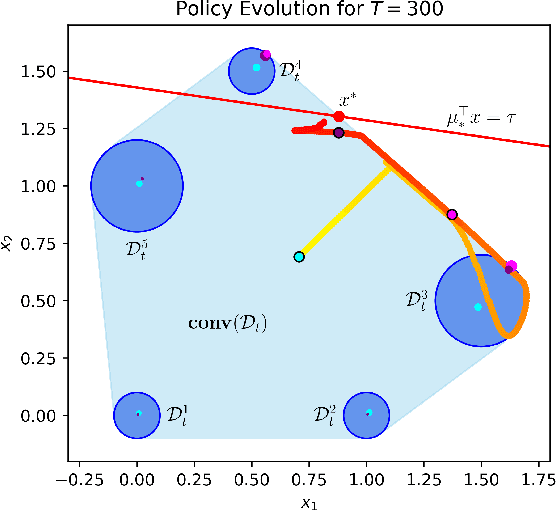
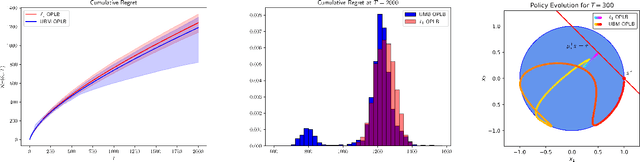
Recently, bandit optimization has received significant attention in real-world safety-critical systems that involve repeated interactions with humans. While there exist various algorithms with performance guarantees in the literature, practical implementation of the algorithms has not received as much attention. This work presents a comprehensive study on the computational aspects of safe bandit algorithms, specifically safe linear bandits, by introducing a framework that leverages convex programming tools to create computationally efficient policies. In particular, we first characterize the properties of the optimal policy for safe linear bandit problem and then propose an end-to-end pipeline of safe linear bandit algorithms that only involves solving convex problems. We also numerically evaluate the performance of our proposed methods.