Model-free Reinforcement Learning for Model-based Control: Towards Safe, Interpretable and Sample-efficient Agents

Training sophisticated agents for optimal decision-making under uncertainty has been key to the rapid development of modern autonomous systems across fields. Notably, model-free reinforcement learning (RL) has enabled decision-making agents to improve their performance directly through system interactions, with minimal prior knowledge about the system. Yet, model-free RL has generally relied on agents equipped with deep neural network function approximators, appealing to the networks' expressivity to capture the agent's policy and value function for complex systems. However, neural networks amplify the issues of sample inefficiency, unsafe learning, and limited interpretability in model-free RL. To this end, this work introduces model-based agents as a compelling alternative for control policy approximation, leveraging adaptable models of system dynamics, cost, and constraints for safe policy learning. These models can encode prior system knowledge to inform, constrain, and aid in explaining the agent's decisions, while deficiencies due to model mismatch can be remedied with model-free RL. We outline the benefits and challenges of learning model-based agents -- exemplified by model predictive control -- and detail the primary learning approaches: Bayesian optimization, policy search RL, and offline strategies, along with their respective strengths. While model-free RL has long been established, its interplay with model-based agents remains largely unexplored, motivating our perspective on their combined potentials for sample-efficient learning of safe and interpretable decision-making agents.

Towards Scalable Bayesian Optimization via Gradient-Informed Bayesian Neural Networks

Bayesian optimization (BO) is a widely used method for data-driven optimization that generally relies on zeroth-order data of objective function to construct probabilistic surrogate models. These surrogates guide the exploration-exploitation process toward finding global optimum. While Gaussian processes (GPs) are commonly employed as surrogates of the unknown objective function, recent studies have highlighted the potential of Bayesian neural networks (BNNs) as scalable and flexible alternatives. Moreover, incorporating gradient observations into GPs, when available, has been shown to improve BO performance. However, the use of gradients within BNN surrogates remains unexplored. By leveraging automatic differentiation, gradient information can be seamlessly integrated into BNN training, resulting in more informative surrogates for BO. We propose a gradient-informed loss function for BNN training, effectively augmenting function observations with local gradient information. The effectiveness of this approach is demonstrated on well-known benchmarks in terms of improved BNN predictions and faster BO convergence as the number of decision variables increases.

MPCritic: A plug-and-play MPC architecture for reinforcement learning

The reinforcement learning (RL) and model predictive control (MPC) communities have developed vast ecosystems of theoretical approaches and computational tools for solving optimal control problems. Given their conceptual similarities but differing strengths, there has been increasing interest in synergizing RL and MPC. However, existing approaches tend to be limited for various reasons, including computational cost of MPC in an RL algorithm and software hurdles towards seamless integration of MPC and RL tools. These challenges often result in the use of "simple" MPC schemes or RL algorithms, neglecting the state-of-the-art in both areas. This paper presents MPCritic, a machine learning-friendly architecture that interfaces seamlessly with MPC tools. MPCritic utilizes the loss landscape defined by a parameterized MPC problem, focusing on "soft" optimization over batched training steps; thereby updating the MPC parameters while avoiding costly minimization and parametric sensitivities. Since the MPC structure is preserved during training, an MPC agent can be readily used for online deployment, where robust constraint satisfaction is paramount. We demonstrate the versatility of MPCritic, in terms of MPC architectures and RL algorithms that it can accommodate, on classic control benchmarks.

LLM Test Generation via Iterative Hybrid Program Analysis

Automating unit test generation remains a significant challenge, particularly for complex methods in real-world projects. While Large Language Models (LLMs) have made strides in code generation, they struggle to achieve high branch coverage due to their limited ability to reason about intricate control flow structures. To address this limitation, we introduce Panta, a technique that emulates the iterative process human developers follow when analyzing code and constructing test cases. Panta integrates static control flow analysis and dynamic code coverage analysis to systematically guide LLMs in identifying uncovered execution paths and generating better test cases. By incorporating an iterative feedback-driven mechanism, our technique continuously refines test generation based on static and dynamic path coverage insights, ensuring more comprehensive and effective testing. Our empirical evaluation, conducted on classes with high cyclomatic complexity from open-source projects, demonstrates that Panta achieves 26% higher line coverage and 23% higher branch coverage compared to the state-of-the-art.

User-Preference Meets Pareto-Optimality: Multi-Objective Bayesian Optimization with Local Gradient Search

Incorporating user preferences into multi-objective Bayesian optimization (MOBO) allows for personalization of the optimization procedure. Preferences are often abstracted in the form of an unknown utility function, estimated through pairwise comparisons of potential outcomes. However, utility-driven MOBO methods can yield solutions that are dominated by nearby solutions, as non-dominance is not enforced. Additionally, classical MOBO commonly relies on estimating the entire Pareto-front to identify the Pareto-optimal solutions, which can be expensive and ignore user preferences. Here, we present a new method, termed preference-utility-balanced MOBO (PUB-MOBO), that allows users to disambiguate between near-Pareto candidate solutions. PUB-MOBO combines utility-based MOBO with local multi-gradient descent to refine user-preferred solutions to be near-Pareto-optimal. To this end, we propose a novel preference-dominated utility function that concurrently preserves user-preferences and dominance amongst candidate solutions. A key advantage of PUB-MOBO is that the local search is restricted to a (small) region of the Pareto-front directed by user preferences, alleviating the need to estimate the entire Pareto-front. PUB-MOBO is tested on three synthetic benchmark problems: DTLZ1, DTLZ2 and DH1, as well as on three real-world problems: Vehicle Safety, Conceptual Marine Design, and Car Side Impact. PUB-MOBO consistently outperforms state-of-the-art competitors in terms of proximity to the Pareto-front and utility regret across all the problems.

Imitation Learning of MPC with Neural Networks: Error Guarantees and Sparsification

This paper presents a framework for bounding the approximation error in imitation model predictive controllers utilizing neural networks. Leveraging the Lipschitz properties of these neural networks, we derive a bound that guides dataset design to ensure the approximation error remains at chosen limits. We discuss how this method can be used to design a stable neural network controller with performance guarantees employing existing robust model predictive control approaches for data generation. Additionally, we introduce a training adjustment, which is based on the sensitivities of the optimization problem and reduces dataset density requirements based on the derived bounds. We verify that the proposed augmentation results in improvements to the network's predictive capabilities and a reduction of the Lipschitz constant. Moreover, on a simulated inverted pendulum problem, we show that the approach results in a closer match of the closed-loop behavior between the imitation and the original model predictive controller.

NaviQAte: Functionality-Guided Web Application Navigation

End-to-end web testing is challenging due to the need to explore diverse web application functionalities. Current state-of-the-art methods, such as WebCanvas, are not designed for broad functionality exploration; they rely on specific, detailed task descriptions, limiting their adaptability in dynamic web environments. We introduce NaviQAte, which frames web application exploration as a question-and-answer task, generating action sequences for functionalities without requiring detailed parameters. Our three-phase approach utilizes advanced large language models like GPT-4o for complex decision-making and cost-effective models, such as GPT-4o mini, for simpler tasks. NaviQAte focuses on functionality-guided web application navigation, integrating multi-modal inputs such as text and images to enhance contextual understanding. Evaluations on the Mind2Web-Live and Mind2Web-Live-Abstracted datasets show that NaviQAte achieves a 44.23% success rate in user task navigation and a 38.46% success rate in functionality navigation, representing a 15% and 33% improvement over WebCanvas. These results underscore the effectiveness of our approach in advancing automated web application testing.

Lyapunov Neural ODE Feedback Control Policies

Deep neural networks are increasingly used as an effective way to represent control policies in a wide-range of learning-based control methods. For continuous-time optimal control problems (OCPs), which are central to many decision-making tasks, control policy learning can be cast as a neural ordinary differential equation (NODE) problem wherein state and control constraints are naturally accommodated. This paper presents a Lyapunov-NODE control (L-NODEC) approach to solving continuous-time OCPs for the case of stabilizing a known constrained nonlinear system around a terminal equilibrium point. We propose a Lyapunov loss formulation that incorporates a control-theoretic Lyapunov condition into the problem of learning a state-feedback neural control policy. We establish that L-NODEC ensures exponential stability of the controlled system, as well as its adversarial robustness to uncertain initial conditions. The performance of L-NODEC is illustrated on a benchmark double integrator problem and for optimal control of thermal dose delivery using a cold atmospheric plasma biomedical system. L-NODEC can substantially reduce the inference time necessary to reach the equilibrium state.

Stability-informed Bayesian Optimization for MPC Cost Function Learning

Designing predictive controllers towards optimal closed-loop performance while maintaining safety and stability is challenging. This work explores closed-loop learning for predictive control parameters under imperfect information while considering closed-loop stability. We employ constrained Bayesian optimization to learn a model predictive controller's (MPC) cost function parametrized as a feedforward neural network, optimizing closed-loop behavior as well as minimizing model-plant mismatch. Doing so offers a high degree of freedom and, thus, the opportunity for efficient and global optimization towards the desired and optimal closed-loop behavior. We extend this framework by stability constraints on the learned controller parameters, exploiting the optimal value function of the underlying MPC as a Lyapunov candidate. The effectiveness of the proposed approach is underlined in simulations, highlighting its performance and safety capabilities.

Neural Schrödinger Bridge with Sinkhorn Losses: Application to Data-driven Minimum Effort Control of Colloidal Self-assembly

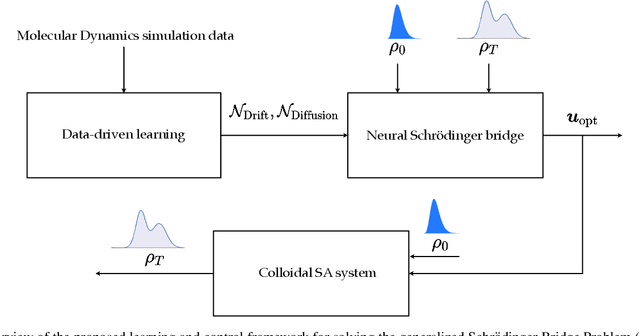
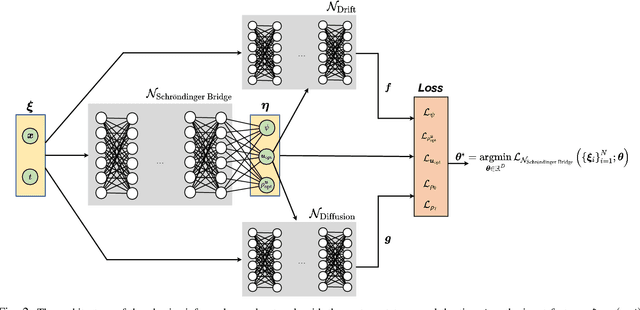
We show that the minimum effort control of colloidal self-assembly can be naturally formulated in the order-parameter space as a generalized Schr\"odinger bridge problem -- a class of fixed-horizon stochastic optimal control problems that originated in the works of Erwin Schr\"odinger in the early 1930s. In recent years, this class of problems has seen a resurgence of research activities in control and machine learning communities. Different from the existing literature on the theory and computation for such problems, the controlled drift and diffusion coefficients for colloidal self-assembly are typically non-affine in control, and are difficult to obtain from physics-based modeling. We deduce the conditions of optimality for such generalized problems, and show that the resulting system of equations is structurally very different from the existing results in a way that standard computational approaches no longer apply. Thus motivated, we propose a data-driven learning and control framework, named `neural Schr\"odinger bridge', to solve such generalized Schr\"odinger bridge problems by innovating on recent advances in neural networks. We illustrate the effectiveness of the proposed framework using a numerical case study of colloidal self-assembly. We learn the controlled drift and diffusion coefficients as two neural networks using molecular dynamics simulation data, and then use these two to train a third network with Sinkhorn losses designed for distributional endpoint constraints, specific for this class of control problems.