Efficient Controller Learning from Human Preferences and Numerical Data Via Multi-Modal Surrogate Models

Tuning control policies manually to meet high-level objectives is often time-consuming. Bayesian optimization provides a data-efficient framework for automating this process using numerical evaluations of an objective function. However, many systems, particularly those involving humans, require optimization based on subjective criteria. Preferential Bayesian optimization addresses this by learning from pairwise comparisons instead of quantitative measurements, but relying solely on preference data can be inefficient. We propose a multi-fidelity, multi-modal Bayesian optimization framework that integrates low-fidelity numerical data with high-fidelity human preferences. Our approach employs Gaussian process surrogate models with both hierarchical, autoregressive and non-hierarchical, coregionalization-based structures, enabling efficient learning from mixed-modality data. We illustrate the framework by tuning an autonomous vehicle's trajectory planner, showing that combining numerical and preference data significantly reduces the need for experiments involving the human decision maker while effectively adapting driving style to individual preferences.

High-Dimensional Surrogate Modeling for Closed-Loop Learning of Neural-Network-Parameterized Model Predictive Control

Learning controller parameters from closed-loop data has been shown to improve closed-loop performance. Bayesian optimization, a widely used black-box and sample-efficient learning method, constructs a probabilistic surrogate of the closed-loop performance from few experiments and uses it to select informative controller parameters. However, it typically struggles with dense high-dimensional controller parameterizations, as they may appear, for example, in tuning model predictive controllers, because standard surrogate models fail to capture the structure of such spaces. This work suggests that the use of Bayesian neural networks as surrogate models may help to mitigate this limitation. Through a comparison between Gaussian processes with Matern kernels, finite-width Bayesian neural networks, and infinite-width Bayesian neural networks on a cart-pole task, we find that Bayesian neural network surrogate models achieve faster and more reliable convergence of the closed-loop cost and enable successful optimization of parameterizations with hundreds of dimensions. Infinite-width Bayesian neural networks also maintain performance in settings with more than one thousand parameters, whereas Matern-kernel Gaussian processes rapidly lose effectiveness. These results indicate that Bayesian neural network surrogate models may be suitable for learning dense high-dimensional controller parameterizations and offer practical guidance for selecting surrogate models in learning-based controller design.

Exploiting Prior Knowledge in Preferential Learning of Individualized Autonomous Vehicle Driving Styles

Trajectory planning for automated vehicles commonly employs optimization over a moving horizon - Model Predictive Control - where the cost function critically influences the resulting driving style. However, finding a suitable cost function that results in a driving style preferred by passengers remains an ongoing challenge. We employ preferential Bayesian optimization to learn the cost function by iteratively querying a passenger's preference. Due to increasing dimensionality of the parameter space, preference learning approaches might struggle to find a suitable optimum with a limited number of experiments and expose the passenger to discomfort when exploring the parameter space. We address these challenges by incorporating prior knowledge into the preferential Bayesian optimization framework. Our method constructs a virtual decision maker from real-world human driving data to guide parameter sampling. In a simulation experiment, we achieve faster convergence of the prior-knowledge-informed learning procedure compared to existing preferential Bayesian optimization approaches and reduce the number of inadequate driving styles sampled.

Time-Series-Informed Closed-loop Learning for Sequential Decision Making and Control

Closed-loop performance of sequential decision making algorithms, such as model predictive control, depends strongly on the parameters of cost functions, models, and constraints. Bayesian optimization is a common approach to learning these parameters based on closed-loop experiments. However, traditional Bayesian optimization approaches treat the learning problem as a black box, ignoring valuable information and knowledge about the structure of the underlying problem, resulting in slow convergence and high experimental resource use. We propose a time-series-informed optimization framework that incorporates intermediate performance evaluations from early iterations of each experimental episode into the learning procedure. Additionally, probabilistic early stopping criteria are proposed to terminate unpromising experiments, significantly reducing experimental time. Simulation results show that our approach achieves baseline performance with approximately half the resources. Moreover, with the same resource budget, our approach outperforms the baseline in terms of final closed-loop performance, highlighting its efficiency in sequential decision making scenarios.

Safe Learning-Based Optimization of Model Predictive Control: Application to Battery Fast-Charging

Model predictive control (MPC) is a powerful tool for controlling complex nonlinear systems under constraints, but often struggles with model uncertainties and the design of suitable cost functions. To address these challenges, we discuss an approach that integrates MPC with safe Bayesian optimization to optimize long-term closed-loop performance despite significant model-plant mismatches. By parameterizing the MPC stage cost function using a radial basis function network, we employ Bayesian optimization as a multi-episode learning strategy to tune the controller without relying on precise system models. This method mitigates conservativeness introduced by overly cautious soft constraints in the MPC cost function and provides probabilistic safety guarantees during learning, ensuring that safety-critical constraints are met with high probability. As a practical application, we apply our approach to fast charging of lithium-ion batteries, a challenging task due to the complicated battery dynamics and strict safety requirements, subject to the requirement to be implementable in real time. Simulation results demonstrate that, in the context of model-plant mismatch, our method reduces charging times compared to traditional MPC methods while maintaining safety. This work extends previous research by emphasizing closed-loop constraint satisfaction and offers a promising solution for enhancing performance in systems where model uncertainties and safety are critical concerns.

Safe and Stable Closed-Loop Learning for Neural-Network-Supported Model Predictive Control

Safe learning of control policies remains challenging, both in optimal control and reinforcement learning. In this article, we consider safe learning of parametrized predictive controllers that operate with incomplete information about the underlying process. To this end, we employ Bayesian optimization for learning the best parameters from closed-loop data. Our method focuses on the system's overall long-term performance in closed-loop while keeping it safe and stable. Specifically, we parametrize the stage cost function of an MPC using a feedforward neural network. This allows for a high degree of flexibility, enabling the system to achieve a better closed-loop performance with respect to a superordinate measure. However, this flexibility also necessitates safety measures, especially with respect to closed-loop stability. To this end, we explicitly incorporated stability information in the Bayesian-optimization-based learning procedure, thereby achieving rigorous probabilistic safety guarantees. The proposed approach is illustrated using a numeric example.

Stability-informed Bayesian Optimization for MPC Cost Function Learning

Designing predictive controllers towards optimal closed-loop performance while maintaining safety and stability is challenging. This work explores closed-loop learning for predictive control parameters under imperfect information while considering closed-loop stability. We employ constrained Bayesian optimization to learn a model predictive controller's (MPC) cost function parametrized as a feedforward neural network, optimizing closed-loop behavior as well as minimizing model-plant mismatch. Doing so offers a high degree of freedom and, thus, the opportunity for efficient and global optimization towards the desired and optimal closed-loop behavior. We extend this framework by stability constraints on the learned controller parameters, exploiting the optimal value function of the underlying MPC as a Lyapunov candidate. The effectiveness of the proposed approach is underlined in simulations, highlighting its performance and safety capabilities.

Learning Model Predictive Control Parameters via Bayesian Optimization for Battery Fast Charging

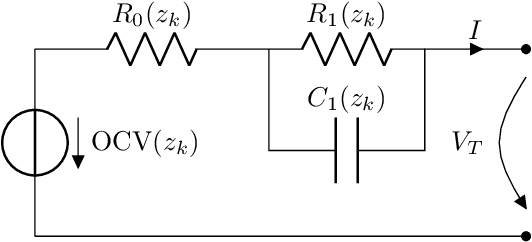
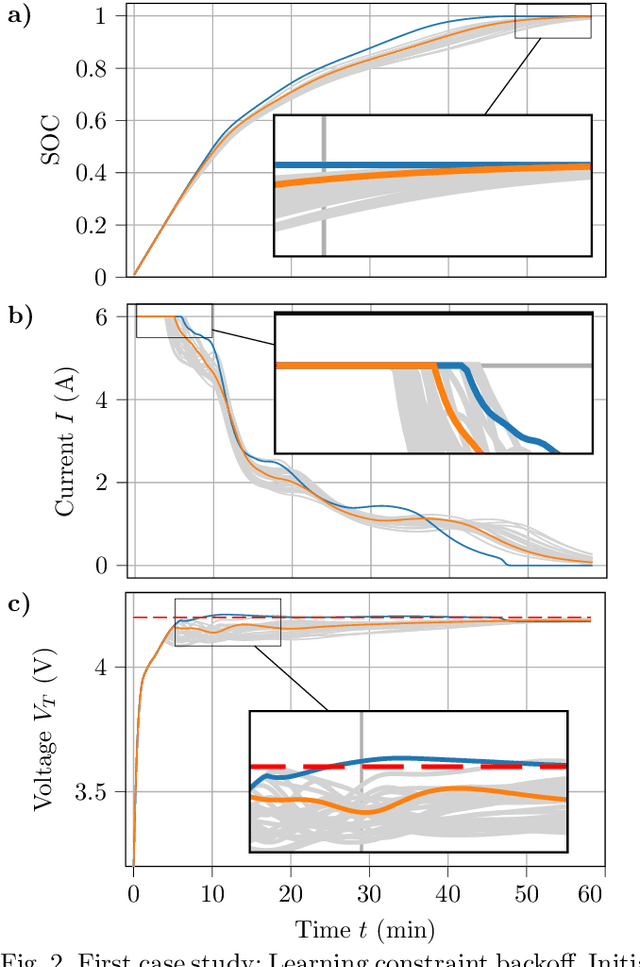
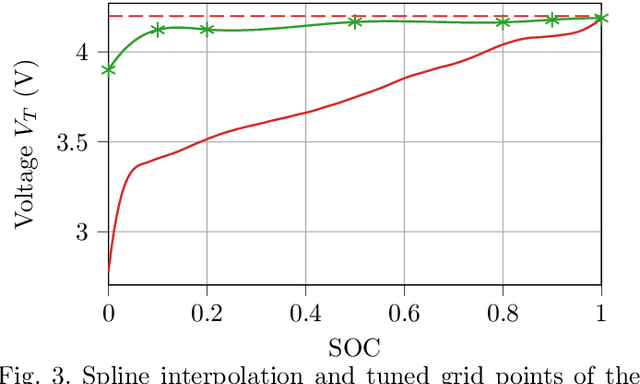
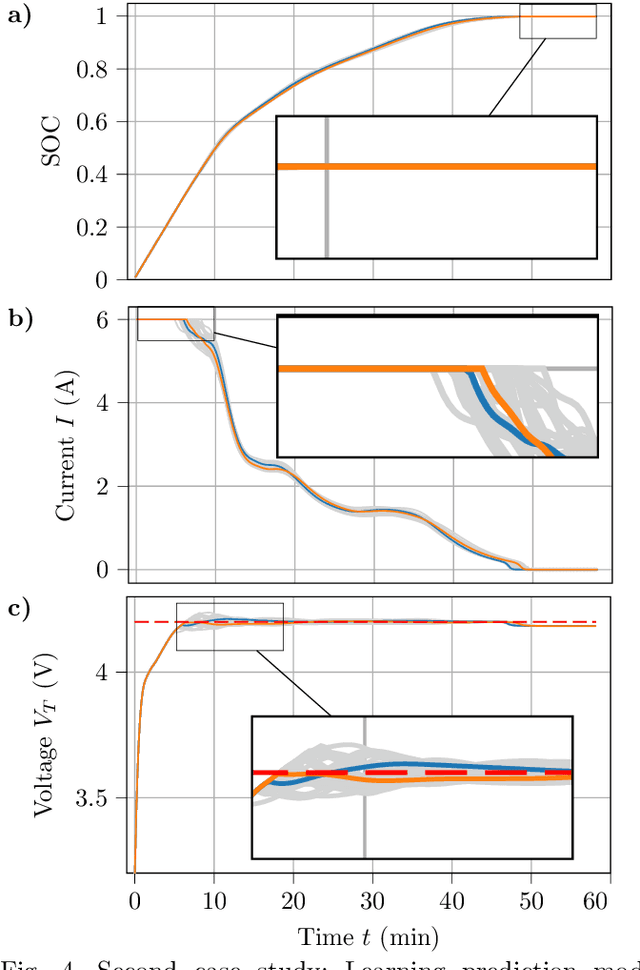
Tuning parameters in model predictive control (MPC) presents significant challenges, particularly when there is a notable discrepancy between the controller's predictions and the actual behavior of the closed-loop plant. This mismatch may stem from factors like substantial model-plant differences, limited prediction horizons that do not cover the entire time of interest, or unforeseen system disturbances. Such mismatches can jeopardize both performance and safety, including constraint satisfaction. Traditional methods address this issue by modifying the finite horizon cost function to better reflect the overall operational cost, learning parts of the prediction model from data, or implementing robust MPC strategies, which might be either computationally intensive or overly cautious. As an alternative, directly optimizing or learning the controller parameters to enhance closed-loop performance has been proposed. We apply Bayesian optimization for efficient learning of unknown model parameters and parameterized constraint backoff terms, aiming to improve closed-loop performance of battery fast charging. This approach establishes a hierarchical control framework where Bayesian optimization directly fine-tunes closed-loop behavior towards a global and long-term objective, while MPC handles lower-level, short-term control tasks. For lithium-ion battery fast charging, we show that the learning approach not only ensures safe operation but also maximizes closed-loop performance. This includes maintaining the battery's operation below its maximum terminal voltage and reducing charging times, all achieved using a standard nominal MPC model with a short horizon and notable initial model-plant mismatch.