Exploiting Prior Knowledge in Preferential Learning of Individualized Autonomous Vehicle Driving Styles

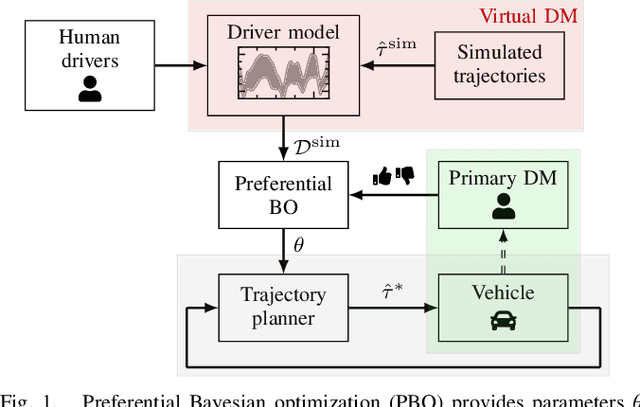
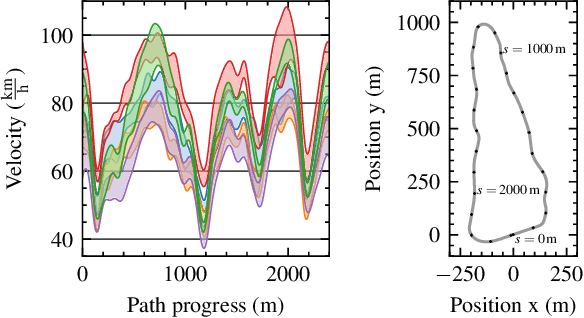
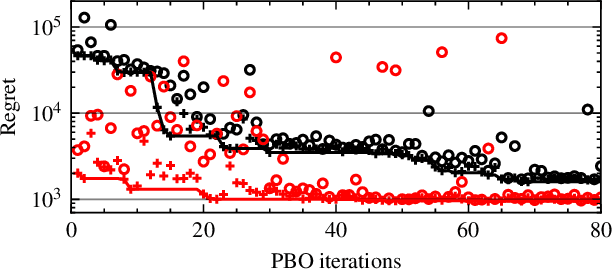
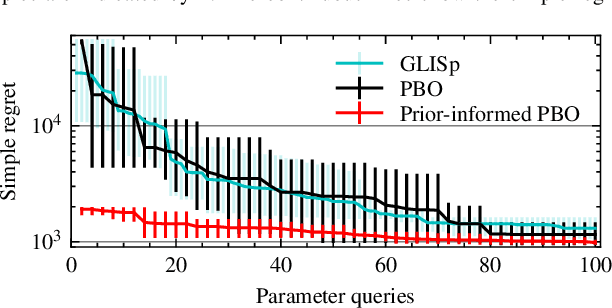
Trajectory planning for automated vehicles commonly employs optimization over a moving horizon - Model Predictive Control - where the cost function critically influences the resulting driving style. However, finding a suitable cost function that results in a driving style preferred by passengers remains an ongoing challenge. We employ preferential Bayesian optimization to learn the cost function by iteratively querying a passenger's preference. Due to increasing dimensionality of the parameter space, preference learning approaches might struggle to find a suitable optimum with a limited number of experiments and expose the passenger to discomfort when exploring the parameter space. We address these challenges by incorporating prior knowledge into the preferential Bayesian optimization framework. Our method constructs a virtual decision maker from real-world human driving data to guide parameter sampling. In a simulation experiment, we achieve faster convergence of the prior-knowledge-informed learning procedure compared to existing preferential Bayesian optimization approaches and reduce the number of inadequate driving styles sampled.

Imitation Learning of MPC with Neural Networks: Error Guarantees and Sparsification

This paper presents a framework for bounding the approximation error in imitation model predictive controllers utilizing neural networks. Leveraging the Lipschitz properties of these neural networks, we derive a bound that guides dataset design to ensure the approximation error remains at chosen limits. We discuss how this method can be used to design a stable neural network controller with performance guarantees employing existing robust model predictive control approaches for data generation. Additionally, we introduce a training adjustment, which is based on the sensitivities of the optimization problem and reduces dataset density requirements based on the derived bounds. We verify that the proposed augmentation results in improvements to the network's predictive capabilities and a reduction of the Lipschitz constant. Moreover, on a simulated inverted pendulum problem, we show that the approach results in a closer match of the closed-loop behavior between the imitation and the original model predictive controller.

Time-Series-Informed Closed-loop Learning for Sequential Decision Making and Control

Closed-loop performance of sequential decision making algorithms, such as model predictive control, depends strongly on the parameters of cost functions, models, and constraints. Bayesian optimization is a common approach to learning these parameters based on closed-loop experiments. However, traditional Bayesian optimization approaches treat the learning problem as a black box, ignoring valuable information and knowledge about the structure of the underlying problem, resulting in slow convergence and high experimental resource use. We propose a time-series-informed optimization framework that incorporates intermediate performance evaluations from early iterations of each experimental episode into the learning procedure. Additionally, probabilistic early stopping criteria are proposed to terminate unpromising experiments, significantly reducing experimental time. Simulation results show that our approach achieves baseline performance with approximately half the resources. Moreover, with the same resource budget, our approach outperforms the baseline in terms of final closed-loop performance, highlighting its efficiency in sequential decision making scenarios.