Neural Schrödinger Bridge with Sinkhorn Losses: Application to Data-driven Minimum Effort Control of Colloidal Self-assembly

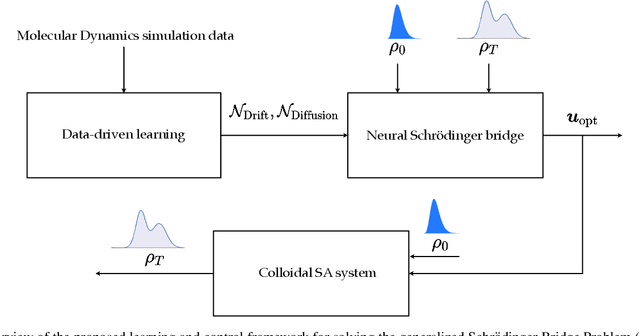
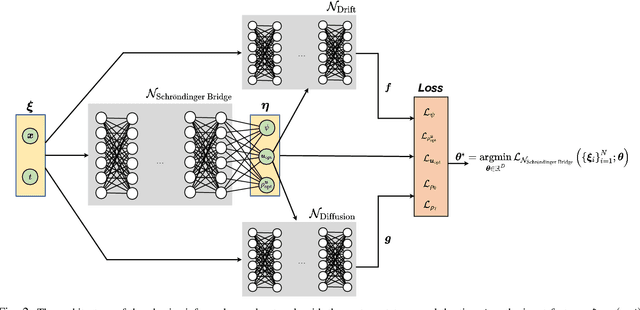
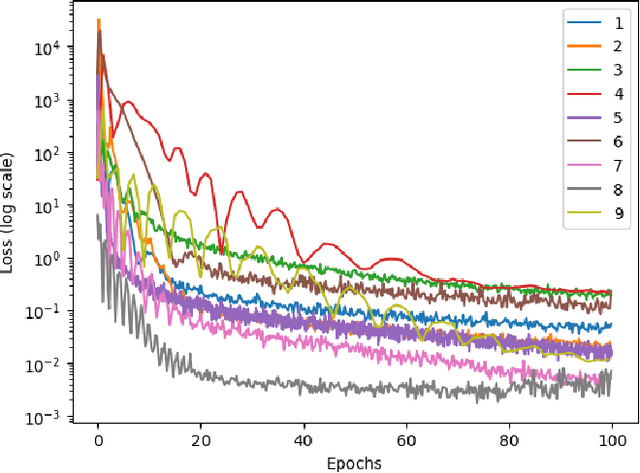
We show that the minimum effort control of colloidal self-assembly can be naturally formulated in the order-parameter space as a generalized Schr\"odinger bridge problem -- a class of fixed-horizon stochastic optimal control problems that originated in the works of Erwin Schr\"odinger in the early 1930s. In recent years, this class of problems has seen a resurgence of research activities in control and machine learning communities. Different from the existing literature on the theory and computation for such problems, the controlled drift and diffusion coefficients for colloidal self-assembly are typically non-affine in control, and are difficult to obtain from physics-based modeling. We deduce the conditions of optimality for such generalized problems, and show that the resulting system of equations is structurally very different from the existing results in a way that standard computational approaches no longer apply. Thus motivated, we propose a data-driven learning and control framework, named `neural Schr\"odinger bridge', to solve such generalized Schr\"odinger bridge problems by innovating on recent advances in neural networks. We illustrate the effectiveness of the proposed framework using a numerical case study of colloidal self-assembly. We learn the controlled drift and diffusion coefficients as two neural networks using molecular dynamics simulation data, and then use these two to train a third network with Sinkhorn losses designed for distributional endpoint constraints, specific for this class of control problems.

Optimal Mass Transport over the Euler Equation

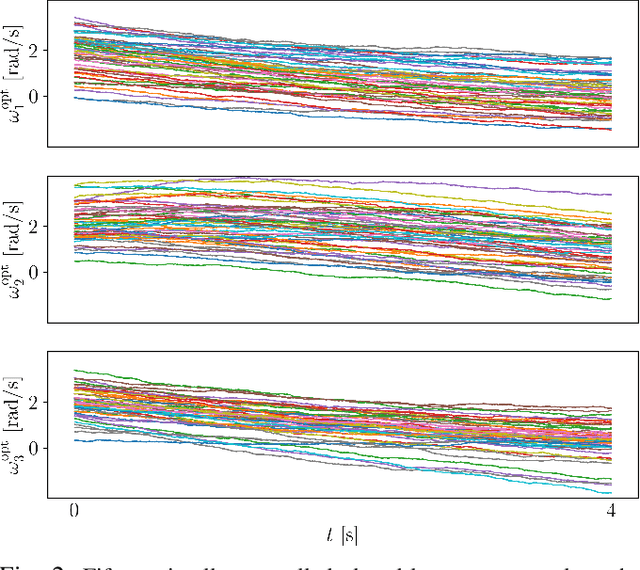
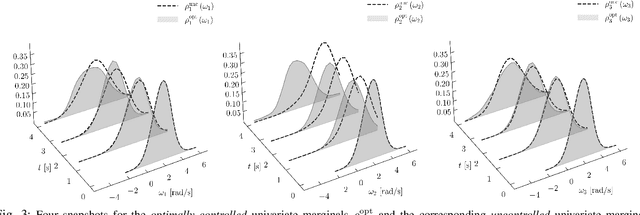
We consider the finite horizon optimal steering of the joint state probability distribution subject to the angular velocity dynamics governed by the Euler equation. The problem and its solution amounts to controlling the spin of a rigid body via feedback, and is of practical importance, for example, in angular stabilization of a spacecraft with stochastic initial and terminal states. We clarify how this problem is an instance of the optimal mass transport (OMT) problem with bilinear prior drift. We deduce both static and dynamic versions of the Eulerian OMT, and provide analytical and numerical results for the synthesis of the optimal controller.