Toroidal Probabilistic Spherical Discriminant Analysis

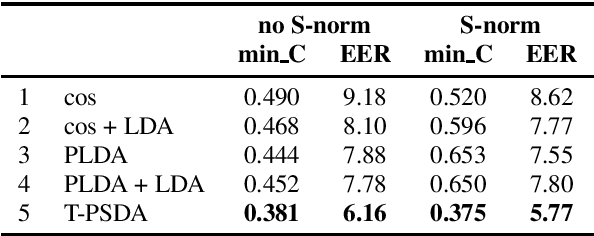
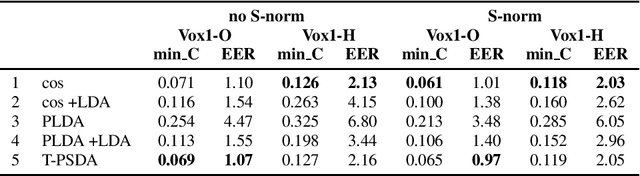
In speaker recognition, where speech segments are mapped to embeddings on the unit hypersphere, two scoring back-ends are commonly used, namely cosine scoring and PLDA. We have recently proposed PSDA, an analog to PLDA that uses Von Mises-Fisher distributions instead of Gaussians. In this paper, we present toroidal PSDA (T-PSDA). It extends PSDA with the ability to model within and between-speaker variabilities in toroidal submanifolds of the hypersphere. Like PLDA and PSDA, the model allows closed-form scoring and closed-form EM updates for training. On VoxCeleb, we find T-PSDA accuracy on par with cosine scoring, while PLDA accuracy is inferior. On NIST SRE'21 we find that T-PSDA gives large accuracy gains compared to both cosine scoring and PLDA.

Probabilistic Spherical Discriminant Analysis: An Alternative to PLDA for length-normalized embeddings

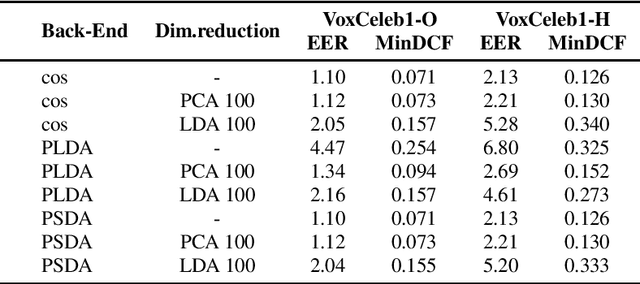
In speaker recognition, where speech segments are mapped to embeddings on the unit hypersphere, two scoring backends are commonly used, namely cosine scoring or PLDA. Both have advantages and disadvantages, depending on the context. Cosine scoring follows naturally from the spherical geometry, but for PLDA the blessing is mixed -- length normalization Gaussianizes the between-speaker distribution, but violates the assumption of a speaker-independent within-speaker distribution. We propose PSDA, an analogue to PLDA that uses Von Mises-Fisher distributions on the hypersphere for both within and between-class distributions. We show how the self-conjugacy of this distribution gives closed-form likelihood-ratio scores, making it a drop-in replacement for PLDA at scoring time. All kinds of trials can be scored, including single-enroll and multi-enroll verification, as well as more complex likelihood-ratios that could be used in clustering and diarization. Learning is done via an EM-algorithm with closed-form updates. We explain the model and present some first experiments.

The Phonexia VoxCeleb Speaker Recognition Challenge 2021 System Description

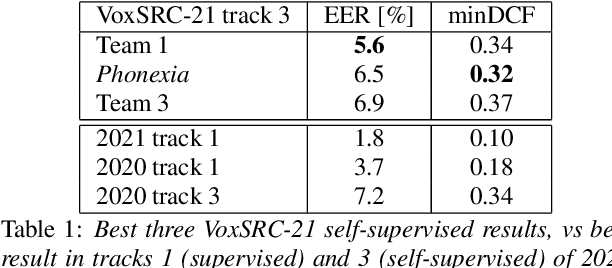
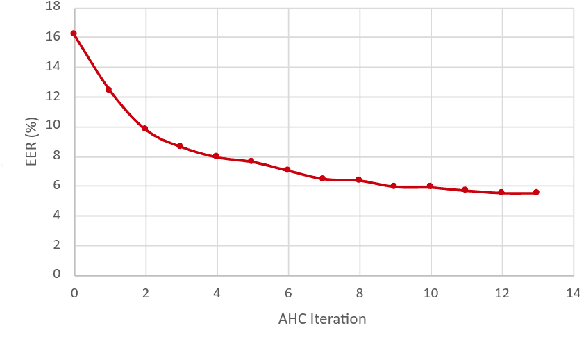
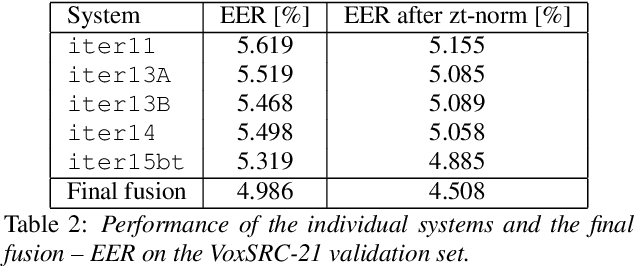
We describe the Phonexia submission for the VoxCeleb Speaker Recognition Challenge 2021 (VoxSRC-21) in the unsupervised speaker verification track. Our solution was very similar to IDLab's winning submission for VoxSRC-20. An embedding extractor was bootstrapped using momentum contrastive learning, with input augmentations as the only source of supervision. This was followed by several iterations of clustering to assign pseudo-speaker labels that were then used for supervised embedding extractor training. Finally, a score fusion was done, by averaging the zt-normalized cosine scores of five different embedding extractors. We briefly also describe unsuccessful solutions involving i-vectors instead of DNN embeddings and PLDA instead of cosine scoring.

Out of a hundred trials, how many errors does your speaker verifier make?

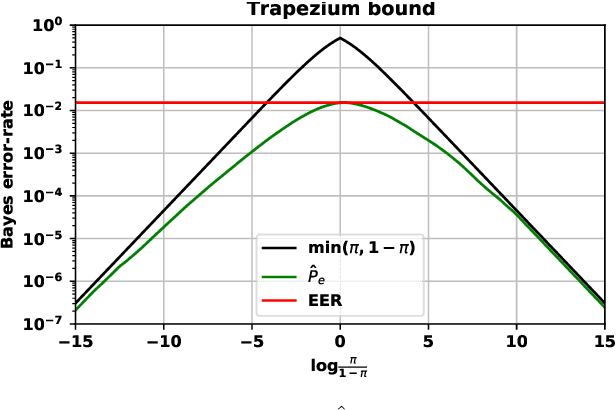
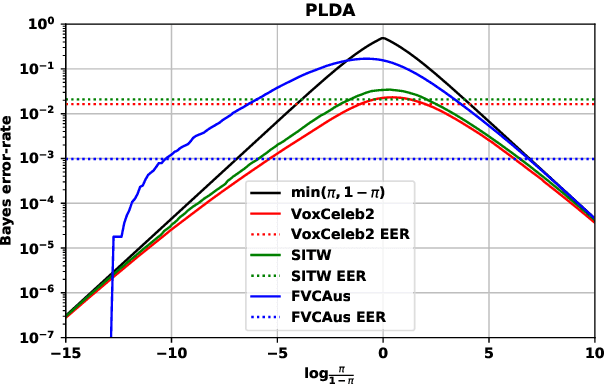
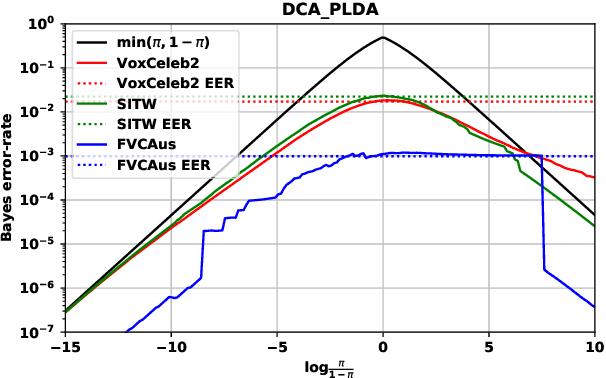
Out of a hundred trials, how many errors does your speaker verifier make? For the user this is an important, practical question, but researchers and vendors typically sidestep it and supply instead the conditional error-rates that are given by the ROC/DET curve. We posit that the user's question is answered by the Bayes error-rate. We present a tutorial to show how to compute the error-rate that results when making Bayes decisions with calibrated likelihood ratios, supplied by the verifier, and an hypothesis prior, supplied by the user. For perfect calibration, the Bayes error-rate is upper bounded by min(EER,P,1-P), where EER is the equal-error-rate and P, 1-P are the prior probabilities of the competing hypotheses. The EER represents the accuracy of the verifier, while min(P,1-P) represents the hardness of the classification problem. We further show how the Bayes error-rate can be computed also for non-perfect calibration and how to generalize from error-rate to expected cost. We offer some criticism of decisions made by direct score thresholding. Finally, we demonstrate by analyzing error-rates of the recently published DCA-PLDA speaker verifier.

Language-depedent I-Vectors for LRE15

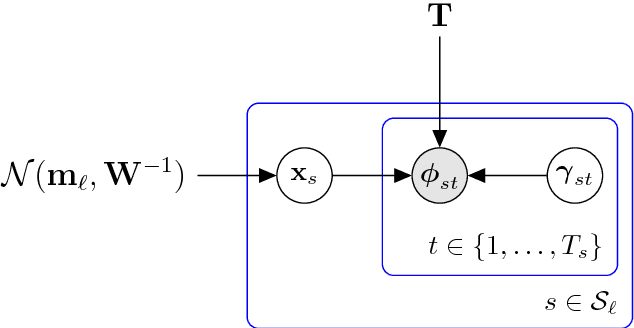
A standard recipe for spoken language recognition is to apply a Gaussian back-end to i-vectors. This ignores the uncertainty in the i-vector extraction, which could be important especially for short utterances. A recent paper by Cumani, Plchot and Fer proposes a solution to propagate that uncertainty into the backend. We propose an alternative method of propagating the uncertainty.

A Generative Model for Score Normalization in Speaker Recognition

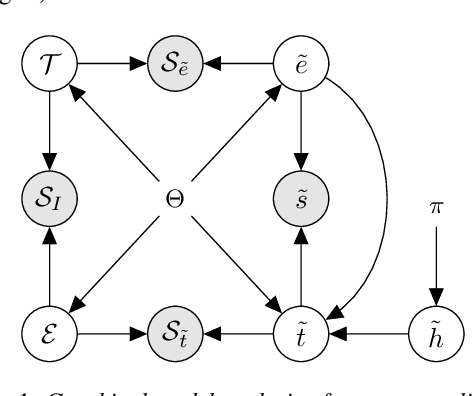
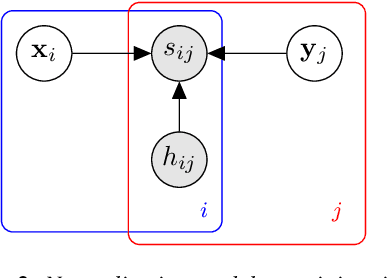
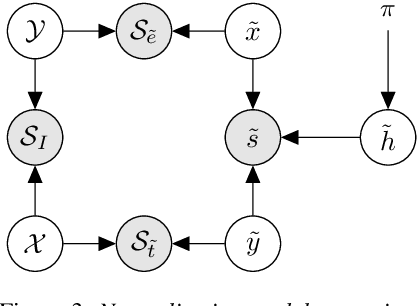
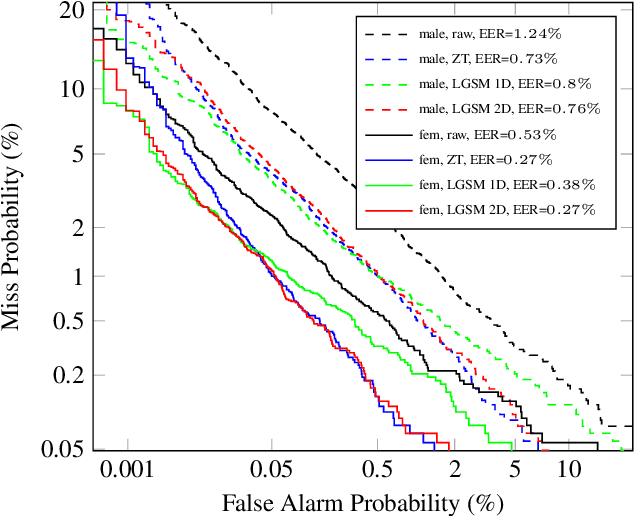
We propose a theoretical framework for thinking about score normalization, which confirms that normalization is not needed under (admittedly fragile) ideal conditions. If, however, these conditions are not met, e.g. under data-set shift between training and runtime, our theory reveals dependencies between scores that could be exploited by strategies such as score normalization. Indeed, it has been demonstrated over and over experimentally, that various ad-hoc score normalization recipes do work. We present a first attempt at using probability theory to design a generative score-space normalization model which gives similar improvements to ZT-norm on the text-dependent RSR 2015 database.

Bayesian calibration for forensic evidence reporting

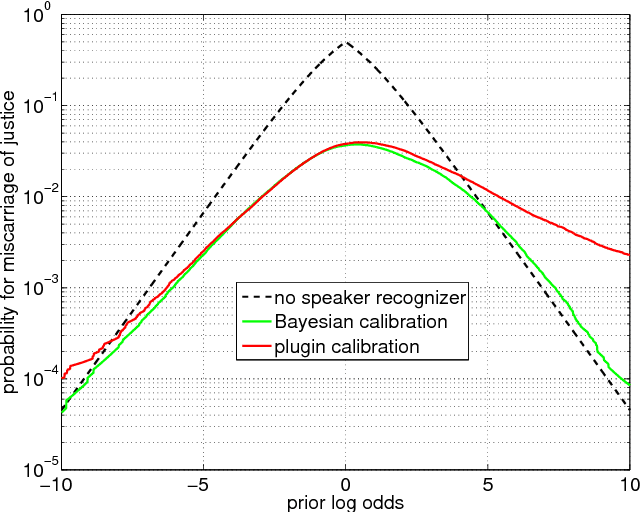
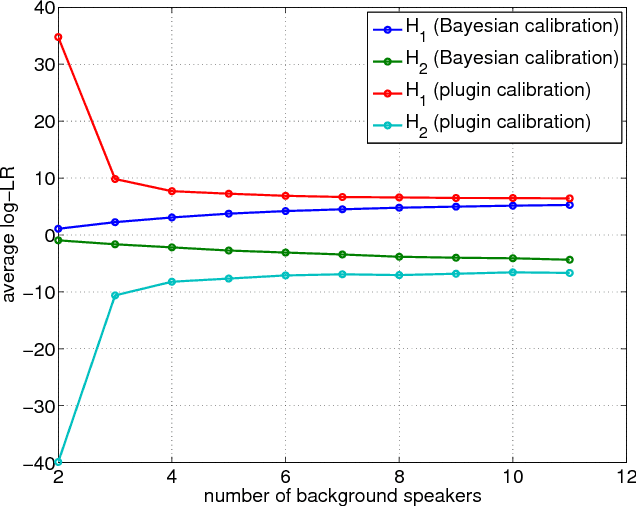
We introduce a Bayesian solution for the problem in forensic speaker recognition, where there may be very little background material for estimating score calibration parameters. We work within the Bayesian paradigm of evidence reporting and develop a principled probabilistic treatment of the problem, which results in a Bayesian likelihood-ratio as the vehicle for reporting weight of evidence. We show in contrast, that reporting a likelihood-ratio distribution does not solve this problem. Our solution is experimentally exercised on a simulated forensic scenario, using NIST SRE'12 scores, which demonstrates a clear advantage for the proposed method compared to the traditional plugin calibration recipe.

A comparison of linear and non-linear calibrations for speaker recognition

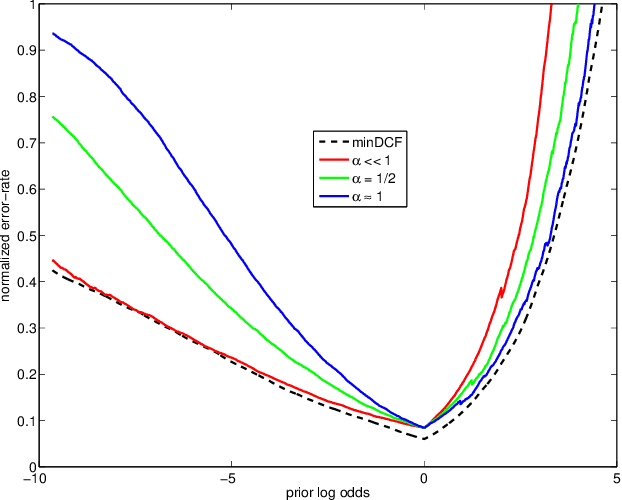
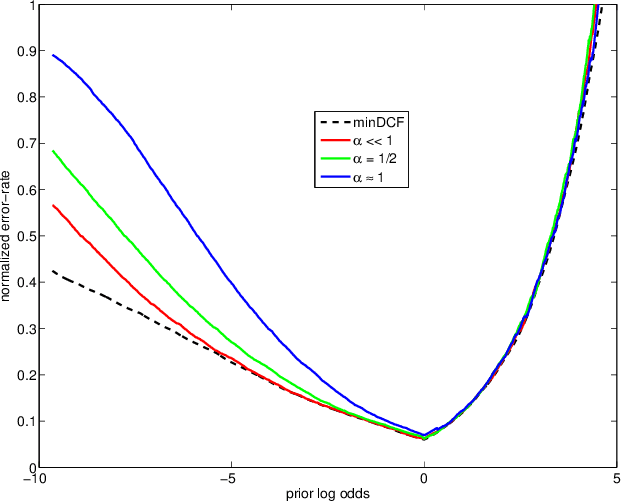
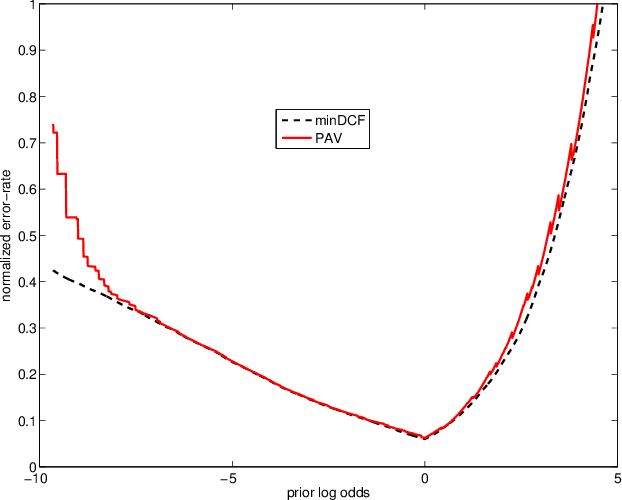
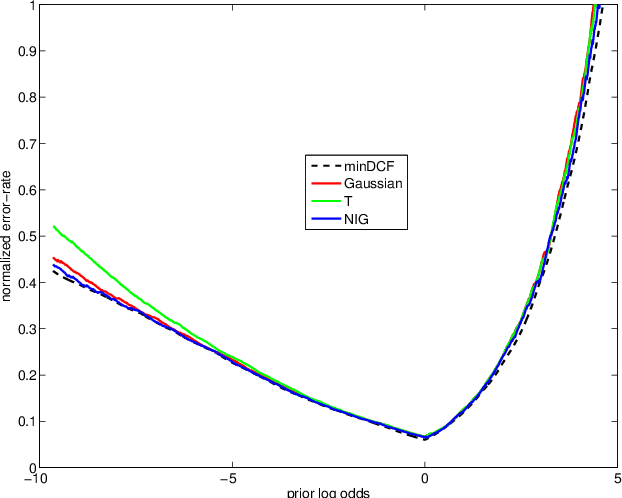
In recent work on both generative and discriminative score to log-likelihood-ratio calibration, it was shown that linear transforms give good accuracy only for a limited range of operating points. Moreover, these methods required tailoring of the calibration training objective functions in order to target the desired region of best accuracy. Here, we generalize the linear recipes to non-linear ones. We experiment with a non-linear, non-parametric, discriminative PAV solution, as well as parametric, generative, maximum-likelihood solutions that use Gaussian, Student's T and normal-inverse-Gaussian score distributions. Experiments on NIST SRE'12 scores suggest that the non-linear methods provide wider ranges of optimal accuracy and can be trained without having to resort to objective function tailoring.