Toroidal Probabilistic Spherical Discriminant Analysis
Paper and Code
Oct 27, 2022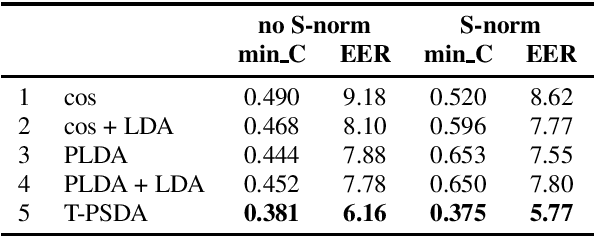
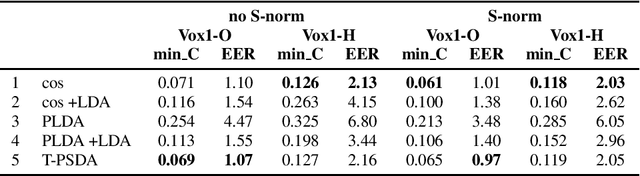
In speaker recognition, where speech segments are mapped to embeddings on the unit hypersphere, two scoring back-ends are commonly used, namely cosine scoring and PLDA. We have recently proposed PSDA, an analog to PLDA that uses Von Mises-Fisher distributions instead of Gaussians. In this paper, we present toroidal PSDA (T-PSDA). It extends PSDA with the ability to model within and between-speaker variabilities in toroidal submanifolds of the hypersphere. Like PLDA and PSDA, the model allows closed-form scoring and closed-form EM updates for training. On VoxCeleb, we find T-PSDA accuracy on par with cosine scoring, while PLDA accuracy is inferior. On NIST SRE'21 we find that T-PSDA gives large accuracy gains compared to both cosine scoring and PLDA.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge