TCIP: Threshold-Controlled Iterative Pyramid Network for Deformable Medical Image Registration

Although pyramid networks have demonstrated superior performance in deformable medical image registration, their decoder architectures are inherently prone to propagating and accumulating anatomical structure misalignments. Moreover, most existing models do not adaptively determine the number of iterations for optimization under varying deformation requirements across images, resulting in either premature termination or excessive iterations that degrades registration accuracy. To effectively mitigate the accumulation of anatomical misalignments, we propose the Feature-Enhanced Residual Module (FERM) as the core component of each decoding layer in the pyramid network. FERM comprises three sequential blocks that extract anatomical semantic features, learn to suppress irrelevant features, and estimate the final deformation field, respectively. To adaptively determine the number of iterations for varying images, we propose the dual-stage Threshold-Controlled Iterative (TCI) strategy. In the first stage, TCI assesses registration stability and with asserted stability, it continues with the second stage to evaluate convergence. We coin the model that integrates FERM and TCI as Threshold-Controlled Iterative Pyramid (TCIP). Extensive experiments on three public brain MRI datasets and one abdomen CT dataset demonstrate that TCIP outperforms the state-of-the-art (SOTA) registration networks in terms of accuracy, while maintaining comparable inference speed and a compact model parameter size. Finally, we assess the generalizability of FERM and TCI by integrating them with existing registration networks and further conduct ablation studies to validate the effectiveness of these two proposed methods.

Weighted Poisson-disk Resampling on Large-Scale Point Clouds

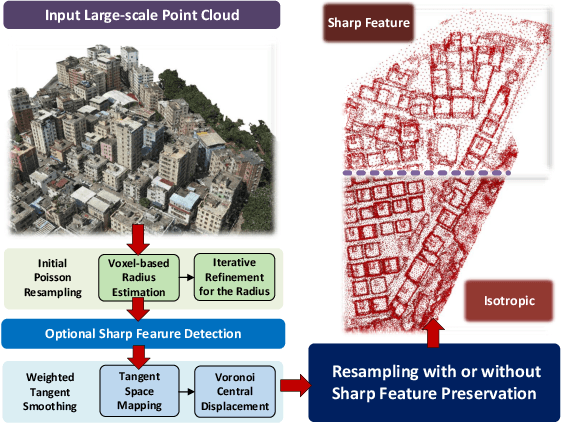
For large-scale point cloud processing, resampling takes the important role of controlling the point number and density while keeping the geometric consistency. % in related tasks. However, current methods cannot balance such different requirements. Particularly with large-scale point clouds, classical methods often struggle with decreased efficiency and accuracy. To address such issues, we propose a weighted Poisson-disk (WPD) resampling method to improve the usability and efficiency for the processing. We first design an initial Poisson resampling with a voxel-based estimation strategy. It is able to estimate a more accurate radius of the Poisson-disk while maintaining high efficiency. Then, we design a weighted tangent smoothing step to further optimize the Voronoi diagram for each point. At the same time, sharp features are detected and kept in the optimized results with isotropic property. Finally, we achieve a resampling copy from the original point cloud with the specified point number, uniform density, and high-quality geometric consistency. Experiments show that our method significantly improves the performance of large-scale point cloud resampling for different applications, and provides a highly practical solution.

Consistent Point Orientation for Manifold Surfaces via Boundary Integration

This paper introduces a new approach for generating globally consistent normals for point clouds sampled from manifold surfaces. Given that the generalized winding number (GWN) field generated by a point cloud with globally consistent normals is a solution to a PDE with jump boundary conditions and possesses harmonic properties, and the Dirichlet energy of the GWN field can be defined as an integral over the boundary surface, we formulate a boundary energy derived from the Dirichlet energy of the GWN. Taking as input a point cloud with randomly oriented normals, we optimize this energy to restore the global harmonicity of the GWN field, thereby recovering the globally consistent normals. Experiments show that our method outperforms state-of-the-art approaches, exhibiting enhanced robustness to noise, outliers, complex topologies, and thin structures. Our code can be found at \url{https://github.com/liuweizhou319/BIM}.