A Surrogate-Assisted Highly Cooperative Coevolutionary Algorithm for Hyperparameter Optimization in Deep Convolutional Neural Network

Convolutional neural networks (CNNs) have gained remarkable success in recent years. However, their performance highly relies on the architecture hyperparameters, and finding proper hyperparameters for a deep CNN is a challenging optimization problem owing to its high-dimensional and computationally expensive characteristics. Given these difficulties, this study proposes a surrogate-assisted highly cooperative hyperparameter optimization (SHCHO) algorithm for chain-styled CNNs. To narrow the large search space, SHCHO first decomposes the whole CNN into several overlapping sub-CNNs in accordance with the overlapping hyperparameter interaction structure and then cooperatively optimizes these hyperparameter subsets. Two cooperation mechanisms are designed during this process. One coordinates all the sub-CNNs to reproduce the information flow in the whole CNN and achieve macro cooperation among them, and the other tackles the overlapping components by simultaneously considering the involved two sub-CNNs and facilitates micro cooperation between them. As a result, a proper hyperparameter configuration can be effectively located for the whole CNN. Besides, SHCHO also employs the well-performing surrogate technique to assist in the hyperparameter optimization of each sub-CNN, thereby greatly reducing the expensive computational cost. Extensive experimental results on two widely-used image classification datasets indicate that SHCHO can significantly improve the performance of CNNs.

Surrogate-assisted cooperative signal optimization for large-scale traffic networks

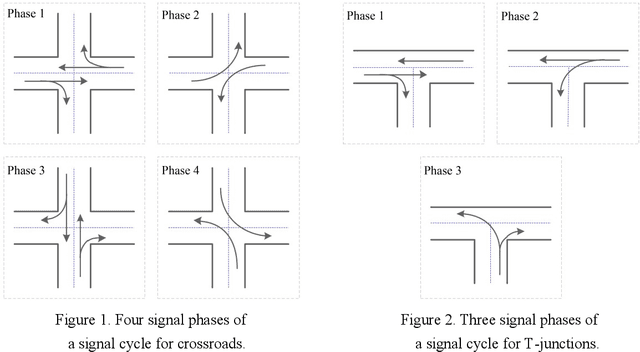
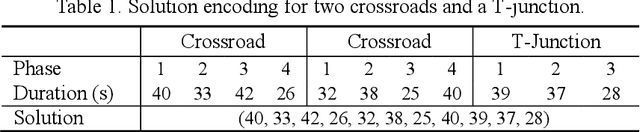
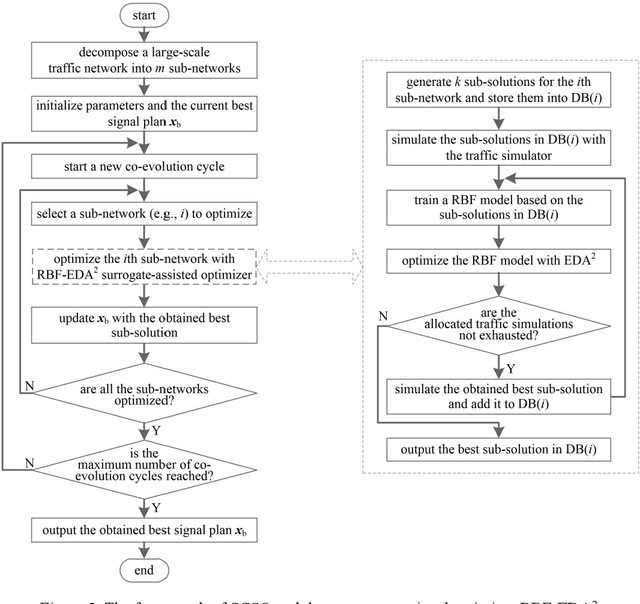
Reasonable setting of traffic signals can be very helpful in alleviating congestion in urban traffic networks. Meta-heuristic optimization algorithms have proved themselves to be able to find high-quality signal timing plans. However, they generally suffer from performance deterioration when solving large-scale traffic signal optimization problems due to the huge search space and limited computational budget. Directing against this issue, this study proposes a surrogate-assisted cooperative signal optimization (SCSO) method. Different from existing methods that directly deal with the entire traffic network, SCSO first decomposes it into a set of tractable sub-networks, and then achieves signal setting by cooperatively optimizing these sub-networks with a surrogate-assisted optimizer. The decomposition operation significantly narrows the search space of the whole traffic network, and the surrogate-assisted optimizer greatly lowers the computational burden by reducing the number of expensive traffic simulations. By taking Newman fast algorithm, radial basis function and a modified estimation of distribution algorithm as decomposer, surrogate model and optimizer, respectively, this study develops a concrete SCSO algorithm. To evaluate its effectiveness and efficiency, a large-scale traffic network involving crossroads and T-junctions is generated based on a real traffic network. Comparison with several existing meta-heuristic algorithms specially designed for traffic signal optimization demonstrates the superiority of SCSO in reducing the average delay time of vehicles.

Enhancing hierarchical surrogate-assisted evolutionary algorithm for high-dimensional expensive optimization via random projection

By remarkably reducing real fitness evaluations, surrogate-assisted evolutionary algorithms (SAEAs), especially hierarchical SAEAs, have been shown to be effective in solving computationally expensive optimization problems. The success of hierarchical SAEAs mainly profits from the potential benefit of their global surrogate models known as "blessing of uncertainty" and the high accuracy of local models. However, their performance leaves room for improvement on highdimensional problems since now it is still challenging to build accurate enough local models due to the huge solution space. Directing against this issue, this study proposes a new hierarchical SAEA by training local surrogate models with the help of the random projection technique. Instead of executing training in the original high-dimensional solution space, the new algorithm first randomly projects training samples onto a set of low-dimensional subspaces, then trains a surrogate model in each subspace, and finally achieves evaluations of candidate solutions by averaging the resulting models. Experimental results on six benchmark functions of 100 and 200 dimensions demonstrate that random projection can significantly improve the accuracy of local surrogate models and the new proposed hierarchical SAEA possesses an obvious edge over state-of-the-art SAEAs

A Surrogate-Assisted Variable Grouping Algorithm for General Large Scale Global Optimization Problems

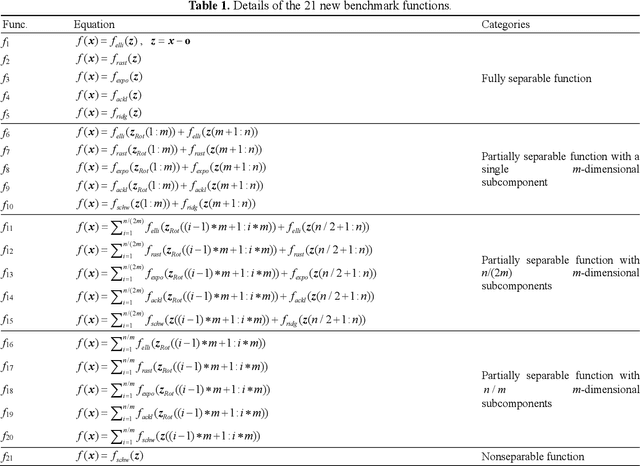
Problem decomposition plays a vital role when applying cooperative coevolution (CC) to large scale global optimization problems. However, most learning-based decomposition algorithms either only apply to additively separable problems or face the issue of false separability detections. Directing against these limitations, this study proposes a novel decomposition algorithm called surrogate-assisted variable grouping (SVG). SVG first designs a general-separability-oriented detection criterion according to whether the optimum of a variable changes with other variables. This criterion is consistent with the separability definition and thus endows SVG with broad applicability and high accuracy. To reduce the fitness evaluation requirement, SVG seeks the optimum of a variable with the help of a surrogate model rather than the original expensive high-dimensional model. Moreover, it converts the variable grouping process into a dynamic-binary-tree search one, which facilitates reutilizing historical separability detection information and thus reducing detection times. To evaluate the performance of SVG, a suite of benchmark functions with up to 2000 dimensions, including additively and non-additively separable ones, were designed. Experimental results on these functions indicate that, compared with six state-of-the-art decomposition algorithms, SVG possesses broader applicability and competitive efficiency. Furthermore, it can significantly enhance the optimization performance of CC.

An Eigenspace Divide-and-Conquer Approach for Large-Scale Optimization

Divide-and-conquer-based (DC-based) evolutionary algorithms (EAs) have achieved notable success in dealing with large-scale optimization problems (LSOPs). However, the appealing performance of this type of algorithms generally requires a high-precision decomposition of the optimization problem, which is still a challenging task for existing decomposition methods. This study attempts to address the above issue from a different perspective and proposes an eigenspace divide-and-conquer (EDC) approach. Different from existing DC-based algorithms that perform decomposition and optimization in the original decision space, EDC first establishes an eigenspace by conducting singular value decomposition on a set of high-quality solutions selected from recent generations. Then it transforms the optimization problem into the eigenspace, and thus significantly weakens the dependencies among the corresponding eigenvariables. Accordingly, these eigenvariables can be efficiently grouped by a simple random strategy and each of the resulting subproblems can be addressed more easily by a traditional EA. To verify the efficiency of EDC, comprehensive experimental studies were conducted on two sets of benchmark functions. Experimental results indicate that EDC is robust to its parameters and has good scalability to the problem dimension. The comparison with several state-of-the-art algorithms further confirms that EDC is pretty competitive and performs better on complicated LSOPs.

Enhancing Gaussian Estimation of Distribution Algorithm by Exploiting Evolution Direction with Archive

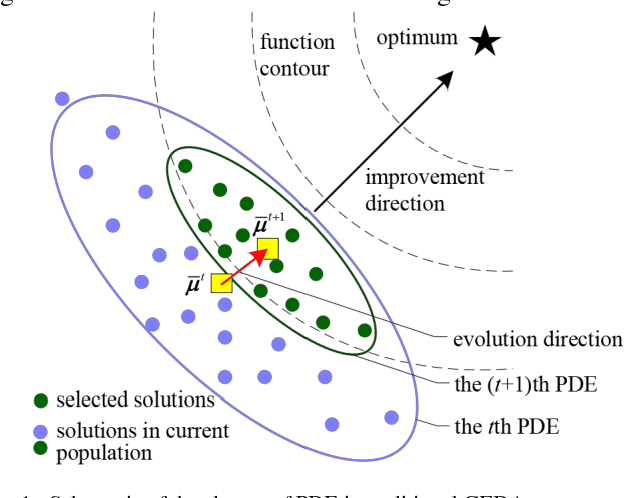
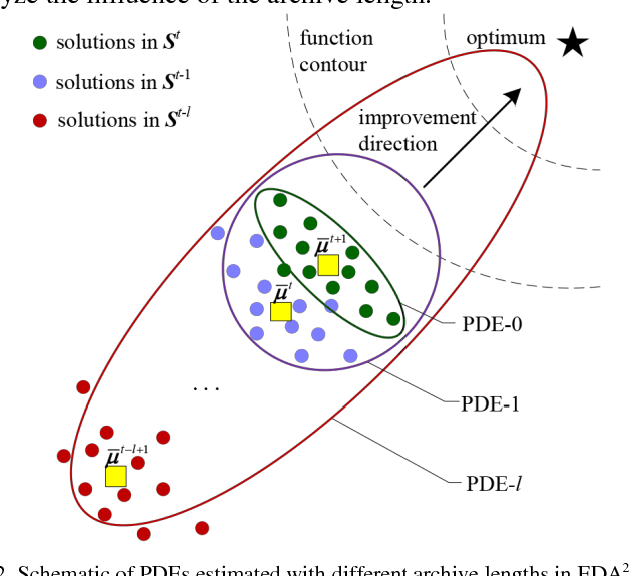
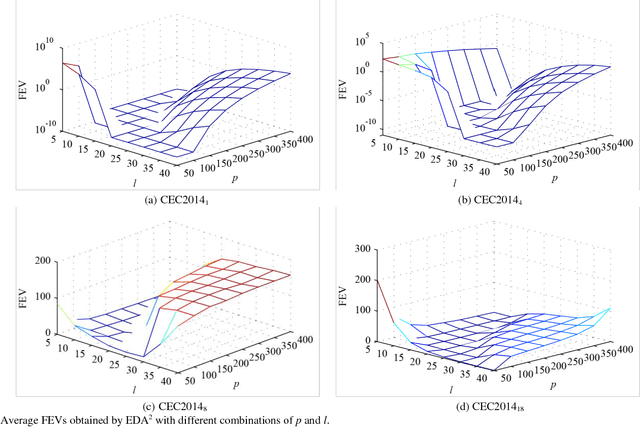
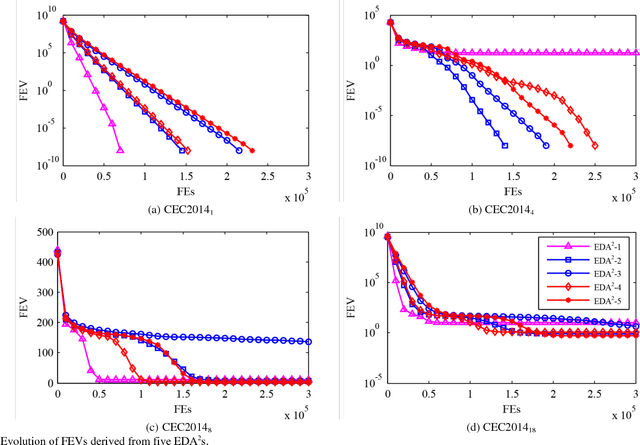
As a typical model-based evolutionary algorithm (EA), estimation of distribution algorithm (EDA) possesses unique characteristics and has been widely applied to global optimization. However, the common-used Gaussian EDA (GEDA) usually suffers from premature convergence which severely limits its search efficiency. This study first systematically analyses the reasons for the deficiency of the traditional GEDA, then tries to enhance its performance by exploiting its evolution direction, and finally develops a new GEDA variant named EDA2. Instead of only utilizing some good solutions produced in the current generation when estimating the Gaussian model, EDA2 preserves a certain number of high-quality solutions generated in previous generations into an archive and takes advantage of these historical solutions to assist estimating the covariance matrix of Gaussian model. By this means, the evolution direction information hidden in the archive is naturally integrated into the estimated model which in turn can guide EDA2 towards more promising solution regions. Moreover, the new estimation method significantly reduces the population size of EDA2 since it needs fewer individuals in the current population for model estimation. As a result, a fast convergence can be achieved. To verify the efficiency of EDA2, we tested it on a variety of benchmark functions and compared it with several state-of-the-art EAs, including IPOP-CMAES, AMaLGaM, three high-powered DE algorithms, and a new PSO algorithm. The experimental results demonstrate that EDA2 is efficient and competitive.

Boosting Cooperative Coevolution for Large Scale Optimization with a Fine-Grained Computation Resource Allocation Strategy

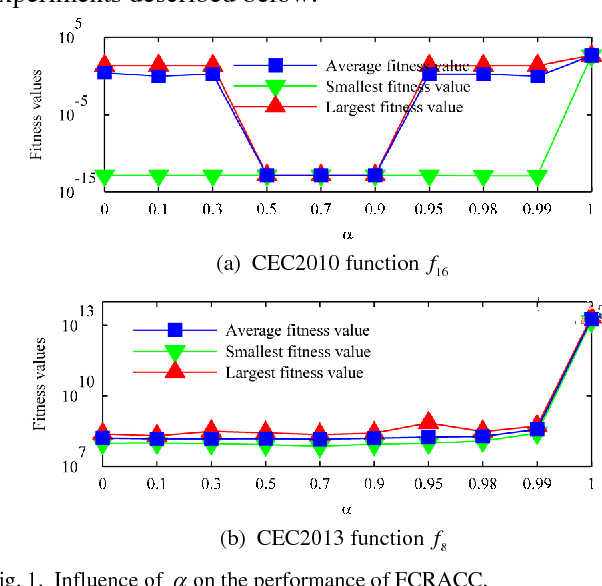
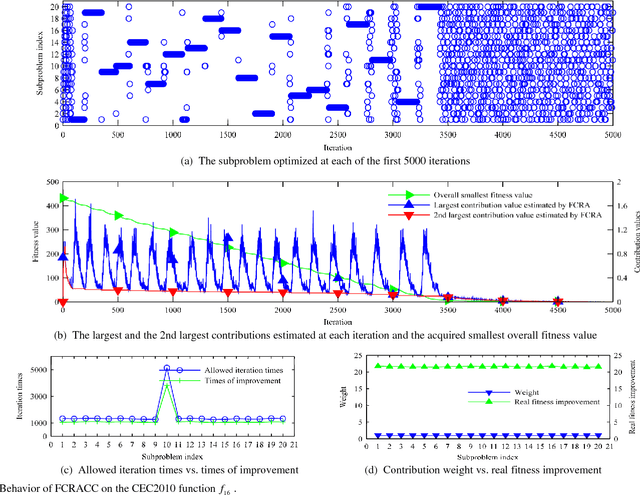
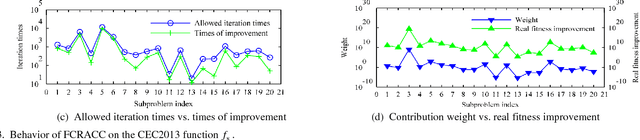
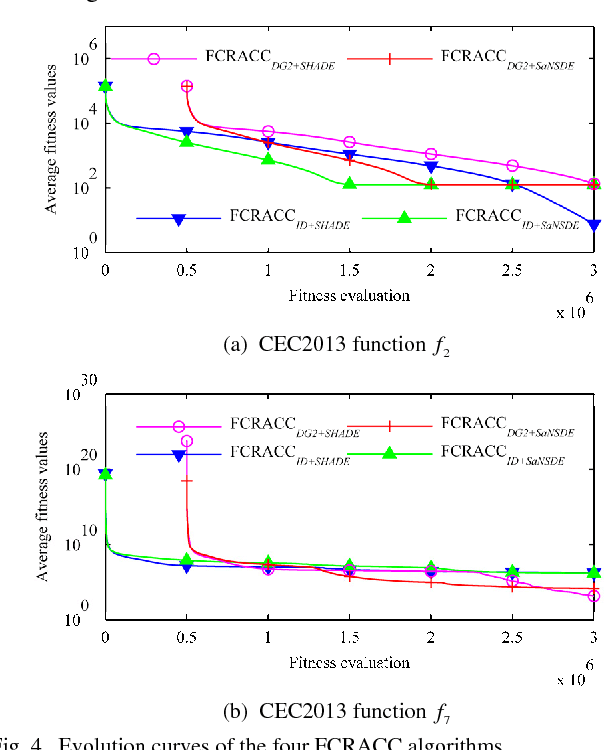
Cooperative coevolution (CC) has shown great potential in solving large scale optimization problems (LSOPs). However, traditional CC algorithms often waste part of computation resource (CR) as they equally allocate CR among all the subproblems. The recently developed contribution-based CC (CBCC) algorithms improve the traditional ones to a certain extent by adaptively allocating CR according to some heuristic rules. Different from existing works, this study explicitly constructs a mathematical model for the CR allocation (CRA) problem in CC and proposes a novel fine-grained CRA (FCRA) strategy by fully considering both the theoretically optimal solution of the CRA model and the evolution characteristics of CC. FCRA takes a single iteration as a basic CRA unit and always selects the subproblem which is most likely to make the largest contribution to the total fitness improvement to undergo a new iteration, where the contribution of a subproblem at a new iteration is estimated according to its current contribution, current evolution status as well as the estimation for its current contribution. We verified the efficiency of FCRA by combining it with SHADE which is an excellent differential evolution variant but has never been employed in the CC framework. Experimental results on two benchmark suites for LSOPs demonstrate that FCRA significantly outperforms existing CRA strategies and the resultant CC algorithm is highly competitive in solving LSOPs.

Niching an Archive-based Gaussian Estimation of Distribution Algorithm via Adaptive Clustering

As a model-based evolutionary algorithm, estimation of distribution algorithm (EDA) possesses unique characteristics and has been widely applied to global optimization. However, traditional Gaussian EDA (GEDA) may suffer from premature convergence and has a high risk of falling into local optimum when dealing with multimodal problem. In this paper, we first attempts to improve the performance of GEDA by utilizing historical solutions and develops a novel archive-based EDA variant. The use of historical solutions not only enhances the search efficiency of EDA to a large extent, but also significantly reduces the population size so that a faster convergence could be achieved. Then, the archive-based EDA is further integrated with a novel adaptive clustering strategy for solving multimodal optimization problems. Taking the advantage of the clustering strategy in locating different promising areas and the powerful exploitation ability of the archive-based EDA, the resultant algorithm is endowed with strong capability in finding multiple optima. To verify the efficiency of the proposed algorithm, we tested it on a set of well-known niching benchmark problems and compared it with several state-of-the-art niching algorithms. The experimental results indicate that the proposed algorithm is competitive.

A Global Information Based Adaptive Threshold for Grouping Large Scale Global Optimization Problems

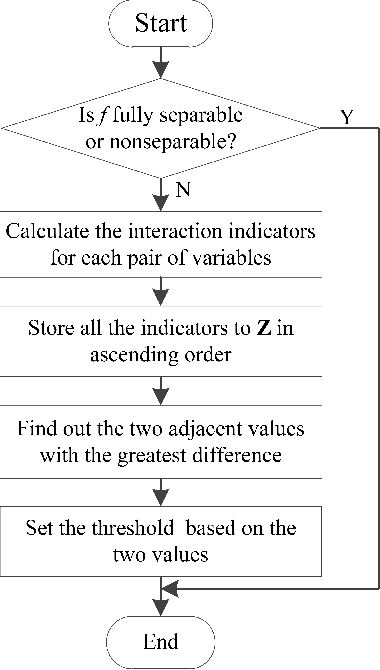
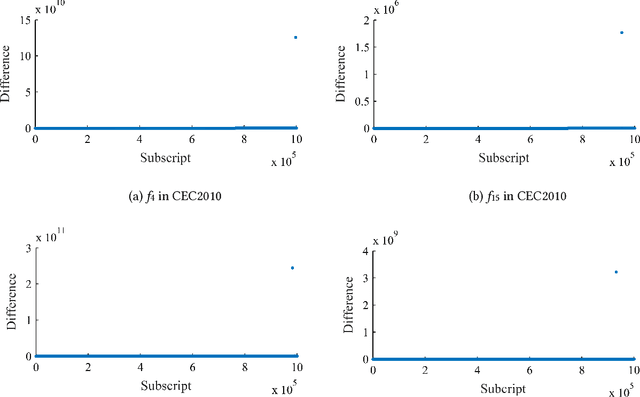
By taking the idea of divide-and-conquer, cooperative coevolution (CC) provides a powerful architecture for large scale global optimization (LSGO) problems, but its efficiency relies highly on the decomposition strategy. It has been shown that differential grouping (DG) performs well on decomposing LSGO problems by effectively detecting the interaction among decision variables. However, its decomposition accuracy depends highly on the threshold. To improve the decomposition accuracy of DG, a global information based adaptive threshold setting algorithm (GIAT) is proposed in this paper. On the one hand, by reducing the sensitivity of the indicator in DG to the roundoff error and the magnitude of contribution weight of subcomponent, we proposed a new indicator for two variables which is much more sensitive to their interaction. On the other hand, instead of setting the threshold only based on one pair of variables, the threshold is generated from the interaction information for all pair of variables. By conducting the experiments on two sets of LSGO benchmark functions, the correctness and robustness of this new indicator and GIAT were verified.

Enhancing Cooperative Coevolution for Large Scale Optimization by Adaptively Constructing Surrogate Models

It has been shown that cooperative coevolution (CC) can effectively deal with large scale optimization problems (LSOPs) through a divide-and-conquer strategy. However, its performance is severely restricted by the current context-vector-based sub-solution evaluation method since this method needs to access the original high dimensional simulation model when evaluating each sub-solution and thus requires many computation resources. To alleviate this issue, this study proposes an adaptive surrogate model assisted CC framework. This framework adaptively constructs surrogate models for different sub-problems by fully considering their characteristics. For the single dimensional sub-problems obtained through decomposition, accurate enough surrogate models can be obtained and used to find out the optimal solutions of the corresponding sub-problems directly. As for the nonseparable sub-problems, the surrogate models are employed to evaluate the corresponding sub-solutions, and the original simulation model is only adopted to reevaluate some good sub-solutions selected by surrogate models. By these means, the computation cost could be greatly reduced without significantly sacrificing evaluation quality. Empirical studies on IEEE CEC 2010 benchmark functions show that the concrete algorithm based on this framework is able to find much better solutions than the conventional CC algorithms and a non-CC algorithm even with much fewer computation resources.