Zuren Feng
Enhancing Gaussian Estimation of Distribution Algorithm by Exploiting Evolution Direction with Archive
Jul 31, 2018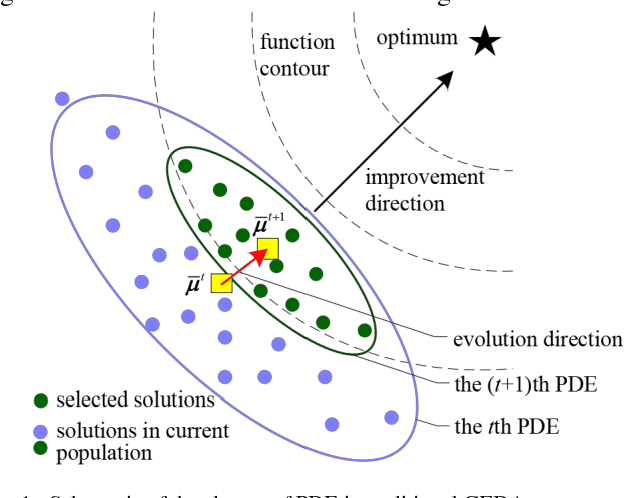
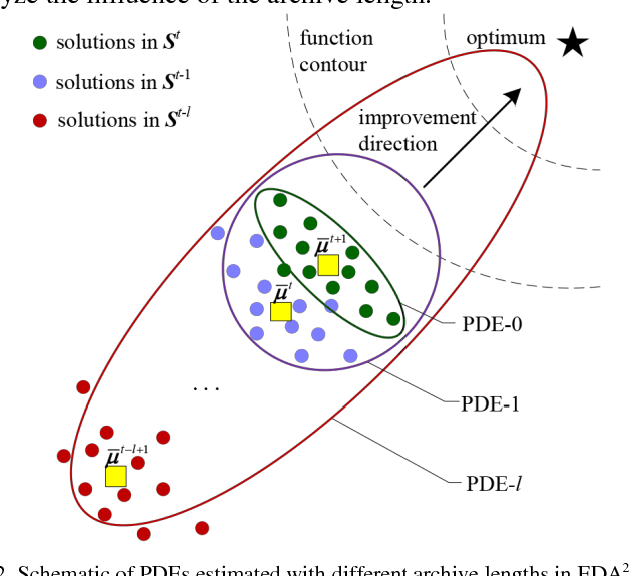
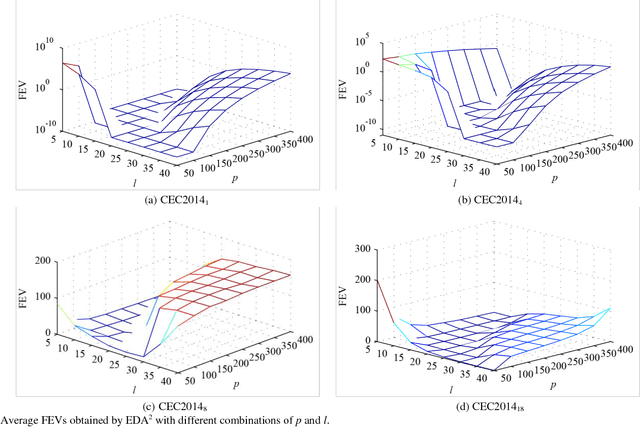
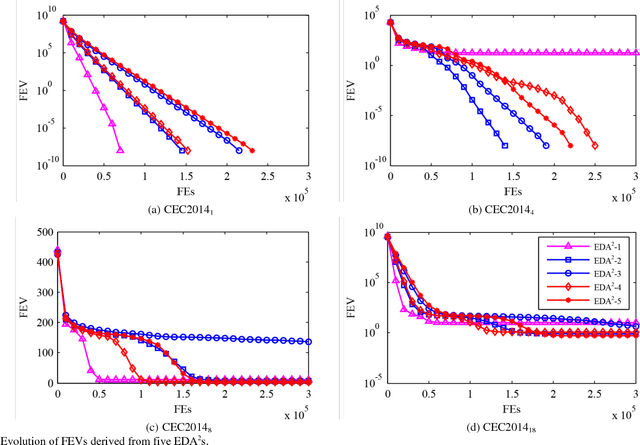
Abstract:As a typical model-based evolutionary algorithm (EA), estimation of distribution algorithm (EDA) possesses unique characteristics and has been widely applied to global optimization. However, the common-used Gaussian EDA (GEDA) usually suffers from premature convergence which severely limits its search efficiency. This study first systematically analyses the reasons for the deficiency of the traditional GEDA, then tries to enhance its performance by exploiting its evolution direction, and finally develops a new GEDA variant named EDA2. Instead of only utilizing some good solutions produced in the current generation when estimating the Gaussian model, EDA2 preserves a certain number of high-quality solutions generated in previous generations into an archive and takes advantage of these historical solutions to assist estimating the covariance matrix of Gaussian model. By this means, the evolution direction information hidden in the archive is naturally integrated into the estimated model which in turn can guide EDA2 towards more promising solution regions. Moreover, the new estimation method significantly reduces the population size of EDA2 since it needs fewer individuals in the current population for model estimation. As a result, a fast convergence can be achieved. To verify the efficiency of EDA2, we tested it on a variety of benchmark functions and compared it with several state-of-the-art EAs, including IPOP-CMAES, AMaLGaM, three high-powered DE algorithms, and a new PSO algorithm. The experimental results demonstrate that EDA2 is efficient and competitive.
Boosting Cooperative Coevolution for Large Scale Optimization with a Fine-Grained Computation Resource Allocation Strategy
Jul 24, 2018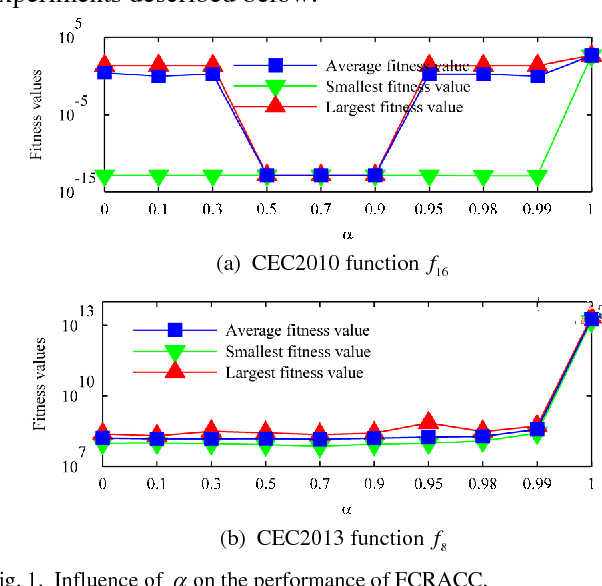
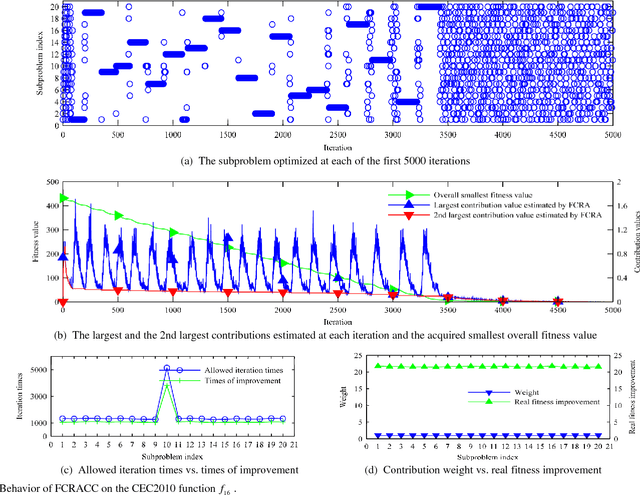
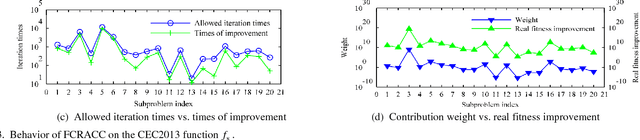
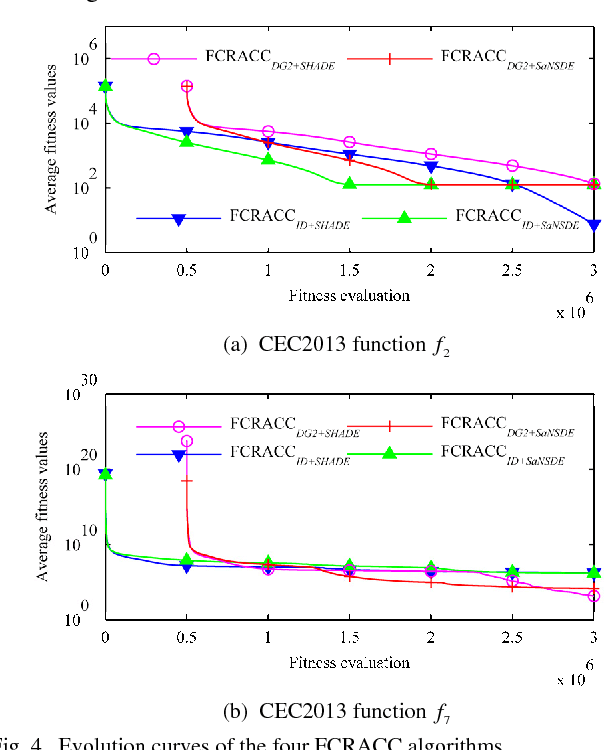
Abstract:Cooperative coevolution (CC) has shown great potential in solving large scale optimization problems (LSOPs). However, traditional CC algorithms often waste part of computation resource (CR) as they equally allocate CR among all the subproblems. The recently developed contribution-based CC (CBCC) algorithms improve the traditional ones to a certain extent by adaptively allocating CR according to some heuristic rules. Different from existing works, this study explicitly constructs a mathematical model for the CR allocation (CRA) problem in CC and proposes a novel fine-grained CRA (FCRA) strategy by fully considering both the theoretically optimal solution of the CRA model and the evolution characteristics of CC. FCRA takes a single iteration as a basic CRA unit and always selects the subproblem which is most likely to make the largest contribution to the total fitness improvement to undergo a new iteration, where the contribution of a subproblem at a new iteration is estimated according to its current contribution, current evolution status as well as the estimation for its current contribution. We verified the efficiency of FCRA by combining it with SHADE which is an excellent differential evolution variant but has never been employed in the CC framework. Experimental results on two benchmark suites for LSOPs demonstrate that FCRA significantly outperforms existing CRA strategies and the resultant CC algorithm is highly competitive in solving LSOPs.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge