On Private Online Convex Optimization: Optimal Algorithms in $\ell_p$-Geometry and High Dimensional Contextual Bandits

Differentially private (DP) stochastic convex optimization (SCO) is ubiquitous in trustworthy machine learning algorithm design. This paper studies the DP-SCO problem with streaming data sampled from a distribution and arrives sequentially. We also consider the continual release model where parameters related to private information are updated and released upon each new data, often known as the online algorithms. Despite that numerous algorithms have been developed to achieve the optimal excess risks in different $\ell_p$ norm geometries, yet none of the existing ones can be adapted to the streaming and continual release setting. To address such a challenge as the online convex optimization with privacy protection, we propose a private variant of online Frank-Wolfe algorithm with recursive gradients for variance reduction to update and reveal the parameters upon each data. Combined with the adaptive differential privacy analysis, our online algorithm achieves in linear time the optimal excess risk when $1<p\leq 2$ and the state-of-the-art excess risk meeting the non-private lower ones when $2<p\leq\infty$. Our algorithm can also be extended to the case $p=1$ to achieve nearly dimension-independent excess risk. While previous variance reduction results on recursive gradient have theoretical guarantee only in the independent and identically distributed sample setting, we establish such a guarantee in a non-stationary setting. To demonstrate the virtues of our method, we design the first DP algorithm for high-dimensional generalized linear bandits with logarithmic regret. Comparative experiments with a variety of DP-SCO and DP-Bandit algorithms exhibit the efficacy and utility of the proposed algorithms.

Generalization Bounds for Stochastic Gradient Langevin Dynamics: A Unified View via Information Leakage Analysis

Recently, generalization bounds of the non-convex empirical risk minimization paradigm using Stochastic Gradient Langevin Dynamics (SGLD) have been extensively studied. Several theoretical frameworks have been presented to study this problem from different perspectives, such as information theory and stability. In this paper, we present a unified view from privacy leakage analysis to investigate the generalization bounds of SGLD, along with a theoretical framework for re-deriving previous results in a succinct manner. Aside from theoretical findings, we conduct various numerical studies to empirically assess the information leakage issue of SGLD. Additionally, our theoretical and empirical results provide explanations for prior works that study the membership privacy of SGLD.

Exploring Private Federated Learning with Laplacian Smoothing

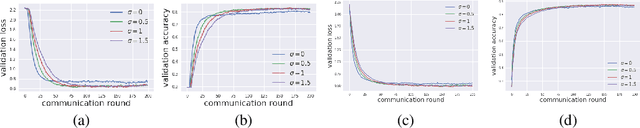
Federated learning aims to protect data privacy by collaboratively learning a model without sharing private data among users. However, an adversary may still be able to infer the private training data by attacking the released model. Differential privacy(DP) provides a statistical guarantee against such attacks, at a privacy of possibly degenerating the accuracy or utility of the trained models. In this paper, we apply a utility enhancement scheme based on Laplacian smoothing for differentially-private federated learning (DP-Fed-LS), where the parameter aggregation with injected Gaussian noise is improved in statistical precision. We provide tight closed-form privacy bounds for both uniform and Poisson subsampling and derive corresponding DP guarantees for differential private federated learning, with or without Laplacian smoothing. Experiments over MNIST, SVHN and Shakespeare datasets show that the proposed method can improve model accuracy with DP-guarantee under both subsampling mechanisms.