Generalization Bounds for Stochastic Gradient Langevin Dynamics: A Unified View via Information Leakage Analysis

Recently, generalization bounds of the non-convex empirical risk minimization paradigm using Stochastic Gradient Langevin Dynamics (SGLD) have been extensively studied. Several theoretical frameworks have been presented to study this problem from different perspectives, such as information theory and stability. In this paper, we present a unified view from privacy leakage analysis to investigate the generalization bounds of SGLD, along with a theoretical framework for re-deriving previous results in a succinct manner. Aside from theoretical findings, we conduct various numerical studies to empirically assess the information leakage issue of SGLD. Additionally, our theoretical and empirical results provide explanations for prior works that study the membership privacy of SGLD.

Generalization in Generative Adversarial Networks: A Novel Perspective from Privacy Protection

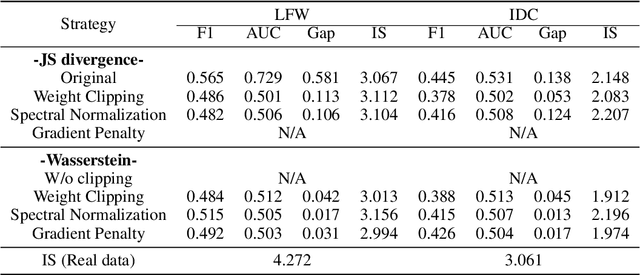
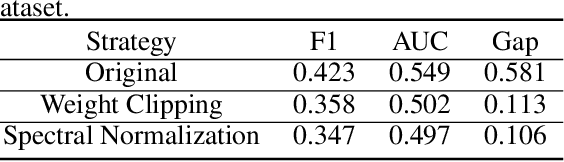
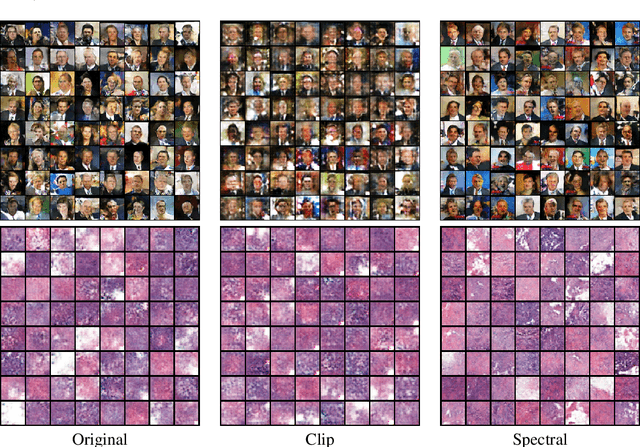
In this paper, we aim to understand the generalization properties of generative adversarial networks (GANs) from a new perspective of privacy protection. Theoretically, we prove that a differentially private learning algorithm used for training the GAN does not overfit to a certain degree, i.e., the generalization gap can be bounded. Moreover, some recent works, such as the Bayesian GAN, can be re-interpreted based on our theoretical insight from privacy protection. Quantitatively, to evaluate the information leakage of well-trained GAN models, we perform various membership attacks on these models. The results show that previous Lipschitz regularization techniques are effective in not only reducing the generalization gap but also alleviating the information leakage of the training dataset.