Zhengdao Wang
Reinforcement Learning Architectures: SAC, TAC, and ESAC
Apr 05, 2020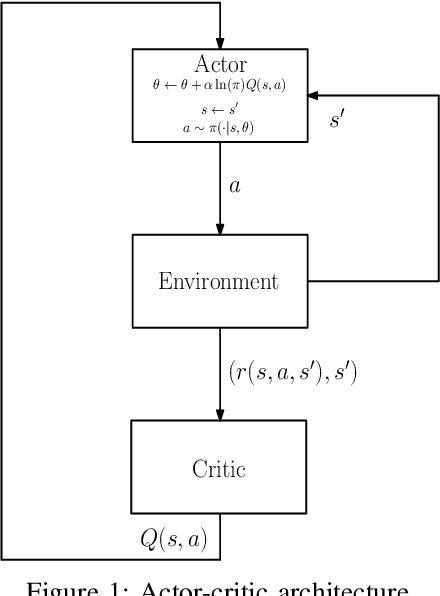
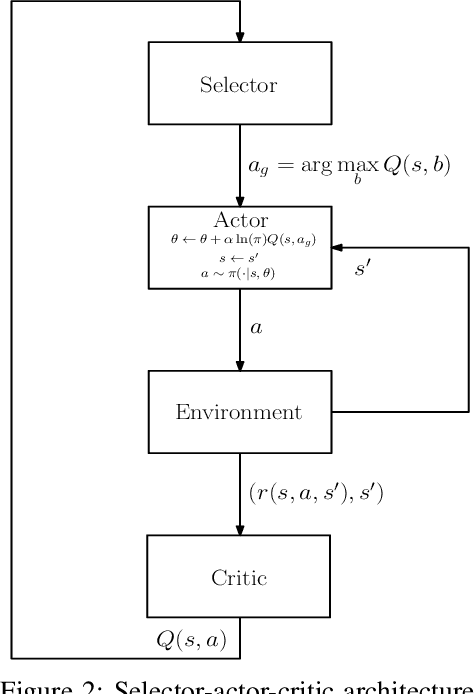
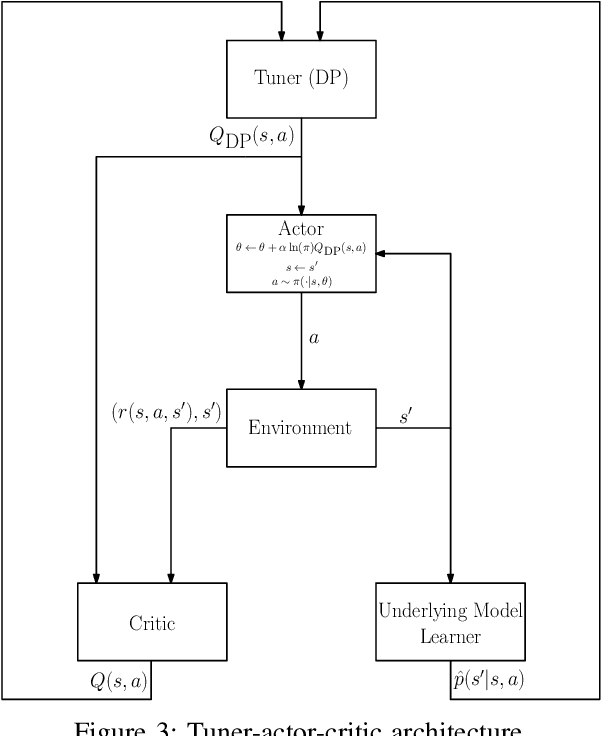

Abstract:The trend is to implement intelligent agents capable of analyzing available information and utilize it efficiently. This work presents a number of reinforcement learning (RL) architectures; one of them is designed for intelligent agents. The proposed architectures are called selector-actor-critic (SAC), tuner-actor-critic (TAC), and estimator-selector-actor-critic (ESAC). These architectures are improved models of a well known architecture in RL called actor-critic (AC). In AC, an actor optimizes the used policy, while a critic estimates a value function and evaluate the optimized policy by the actor. SAC is an architecture equipped with an actor, a critic, and a selector. The selector determines the most promising action at the current state based on the last estimate from the critic. TAC consists of a tuner, a model-learner, an actor, and a critic. After receiving the approximated value of the current state-action pair from the critic and the learned model from the model-learner, the tuner uses the Bellman equation to tune the value of the current state-action pair. ESAC is proposed to implement intelligent agents based on two ideas, which are lookahead and intuition. Lookahead appears in estimating the values of the available actions at the next state, while the intuition appears in maximizing the probability of selecting the most promising action. The newly added elements are an underlying model learner, an estimator, and a selector. The model learner is used to approximate the underlying model. The estimator uses the approximated value function, the learned underlying model, and the Bellman equation to estimate the values of all actions at the next state. The selector is used to determine the most promising action at the next state, which will be used by the actor to optimize the used policy. Finally, the results show the superiority of ESAC compared with the other architectures.
PINE: Universal Deep Embedding for Graph Nodes via Partial Permutation Invariant Set Functions
Sep 25, 2019
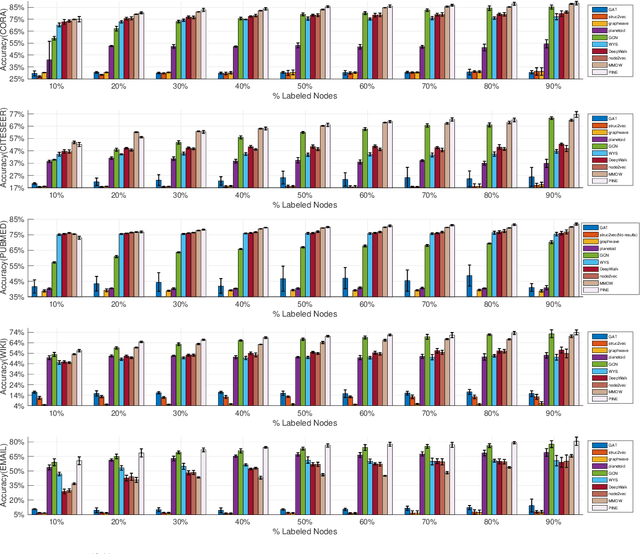


Abstract:Graph node embedding aims at learning a vector representation for all nodes given a graph. It is a central problem in many machine learning tasks (e.g., node classification, recommendation, community detection). The key problem in graph node embedding lies in how to define the dependence to neighbors. Existing approaches specify (either explicitly or implicitly) certain dependencies on neighbors, which may lead to loss of subtle but important structural information within the graph and other dependencies among neighbors. This intrigues us to ask the question: can we design a model to give the maximal flexibility of dependencies to each node's neighborhood. In this paper, we propose a novel graph node embedding (named PINE) via a novel notion of partial permutation invariant set function, to capture any possible dependence. Our method 1) can learn an arbitrary form of the representation function from the neighborhood, withour losing any potential dependence structures, and 2) is applicable to both homogeneous and heterogeneous graph embedding, the latter of which is challenged by the diversity of node types. Furthermore, we provide theoretical guarantee for the representation capability of our method for general homogeneous and heterogeneous graphs. Empirical evaluation results on benchmark data sets show that our proposed PINE method outperforms the state-of-the-art approaches on producing node vectors for various learning tasks of both homogeneous and heterogeneous graphs.
On the Sublinear Convergence of Randomly Perturbed Alternating Gradient Descent to Second Order Stationary Solutions
Feb 28, 2018



Abstract:The alternating gradient descent (AGD) is a simple but popular algorithm which has been applied to problems in optimization, machine learning, data ming, and signal processing, etc. The algorithm updates two blocks of variables in an alternating manner, in which a gradient step is taken on one block, while keeping the remaining block fixed. When the objective function is nonconvex, it is well-known the AGD converges to the first-order stationary solution with a global sublinear rate. In this paper, we show that a variant of AGD-type algorithms will not be trapped by "bad" stationary solutions such as saddle points and local maximum points. In particular, we consider a smooth unconstrained optimization problem, and propose a perturbed AGD (PA-GD) which converges (with high probability) to the set of second-order stationary solutions (SS2) with a global sublinear rate. To the best of our knowledge, this is the first alternating type algorithm which takes $\mathcal{O}(\text{polylog}(d)/\epsilon^{7/3})$ iterations to achieve SS2 with high probability [where polylog$(d)$ is polynomial of the logarithm of dimension $d$ of the problem].
A Nonconvex Splitting Method for Symmetric Nonnegative Matrix Factorization: Convergence Analysis and Optimality
Mar 24, 2017



Abstract:Symmetric nonnegative matrix factorization (SymNMF) has important applications in data analytics problems such as document clustering, community detection and image segmentation. In this paper, we propose a novel nonconvex variable splitting method for solving SymNMF. The proposed algorithm is guaranteed to converge to the set of Karush-Kuhn-Tucker (KKT) points of the nonconvex SymNMF problem. Furthermore, it achieves a global sublinear convergence rate. We also show that the algorithm can be efficiently implemented in parallel. Further, sufficient conditions are provided which guarantee the global and local optimality of the obtained solutions. Extensive numerical results performed on both synthetic and real data sets suggest that the proposed algorithm converges quickly to a local minimum solution.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge