PINE: Universal Deep Embedding for Graph Nodes via Partial Permutation Invariant Set Functions
Paper and Code
Sep 25, 2019
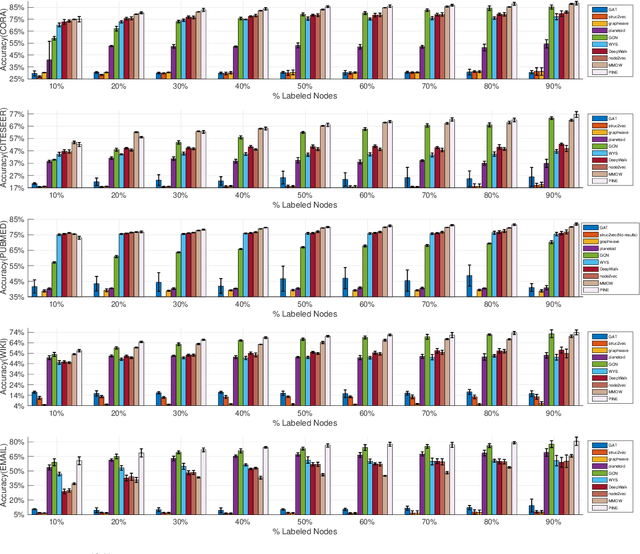
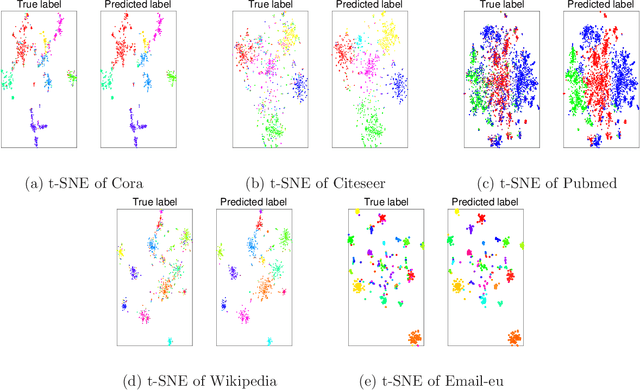

Graph node embedding aims at learning a vector representation for all nodes given a graph. It is a central problem in many machine learning tasks (e.g., node classification, recommendation, community detection). The key problem in graph node embedding lies in how to define the dependence to neighbors. Existing approaches specify (either explicitly or implicitly) certain dependencies on neighbors, which may lead to loss of subtle but important structural information within the graph and other dependencies among neighbors. This intrigues us to ask the question: can we design a model to give the maximal flexibility of dependencies to each node's neighborhood. In this paper, we propose a novel graph node embedding (named PINE) via a novel notion of partial permutation invariant set function, to capture any possible dependence. Our method 1) can learn an arbitrary form of the representation function from the neighborhood, withour losing any potential dependence structures, and 2) is applicable to both homogeneous and heterogeneous graph embedding, the latter of which is challenged by the diversity of node types. Furthermore, we provide theoretical guarantee for the representation capability of our method for general homogeneous and heterogeneous graphs. Empirical evaluation results on benchmark data sets show that our proposed PINE method outperforms the state-of-the-art approaches on producing node vectors for various learning tasks of both homogeneous and heterogeneous graphs.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge