Autonomous Sparse Mean-CVaR Portfolio Optimization

The $\ell_0$-constrained mean-CVaR model poses a significant challenge due to its NP-hard nature, typically tackled through combinatorial methods characterized by high computational demands. From a markedly different perspective, we propose an innovative autonomous sparse mean-CVaR portfolio model, capable of approximating the original $\ell_0$-constrained mean-CVaR model with arbitrary accuracy. The core idea is to convert the $\ell_0$ constraint into an indicator function and subsequently handle it through a tailed approximation. We then propose a proximal alternating linearized minimization algorithm, coupled with a nested fixed-point proximity algorithm (both convergent), to iteratively solve the model. Autonomy in sparsity refers to retaining a significant portion of assets within the selected asset pool during adjustments in pool size. Consequently, our framework offers a theoretically guaranteed approximation of the $\ell_0$-constrained mean-CVaR model, improving computational efficiency while providing a robust asset selection scheme.

A De-singularity Subgradient Approach for the Extended Weber Location Problem

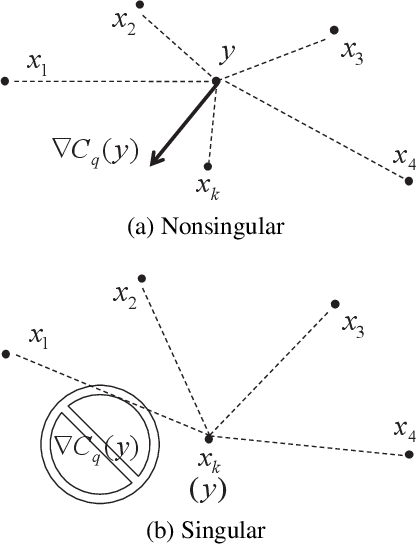
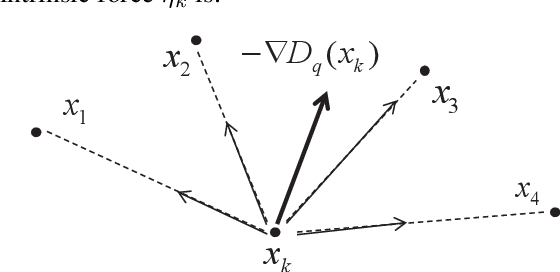
The extended Weber location problem is a classical optimization problem that has inspired some new works in several machine learning scenarios recently. However, most existing algorithms may get stuck due to the singularity at the data points when the power of the cost function $1\leqslant q<2$, such as the widely-used iterative Weiszfeld approach. In this paper, we establish a de-singularity subgradient approach for this problem. We also provide a complete proof of convergence which has fixed some incomplete statements of the proofs for some previous Weiszfeld algorithms. Moreover, we deduce a new theoretical result of superlinear convergence for the iteration sequence in a special case where the minimum point is a singular point. We conduct extensive experiments in a real-world machine learning scenario to show that the proposed approach solves the singularity problem, produces the same results as in the non-singularity cases, and shows a reasonable rate of linear convergence. The results also indicate that the $q$-th power case ($1<q<2$) is more advantageous than the $1$-st power case and the $2$-nd power case in some situations. Hence the de-singularity subgradient approach is beneficial to advancing both theory and practice for the extended Weber location problem.

Invariant Risk Minimization Is A Total Variation Model

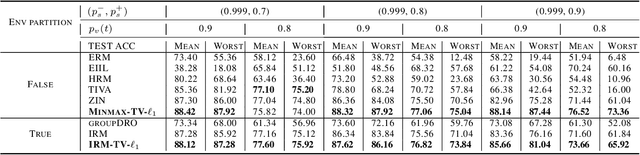
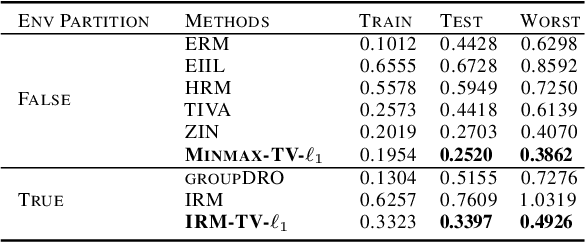
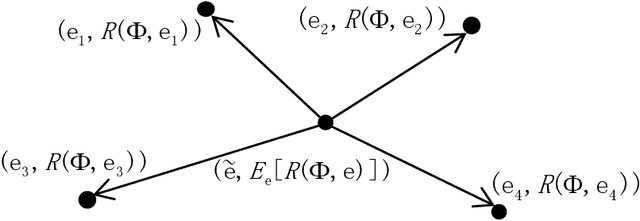
Invariant risk minimization (IRM) is an arising approach to generalize invariant features to different environments in machine learning. While most related works focus on new IRM settings or new application scenarios, the mathematical essence of IRM remains to be properly explained. We verify that IRM is essentially a total variation based on $L^2$ norm (TV-$\ell_2$) of the learning risk with respect to the classifier variable. Moreover, we propose a novel IRM framework based on the TV-$\ell_1$ model. It not only expands the classes of functions that can be used as the learning risk, but also has robust performance in denoising and invariant feature preservation based on the coarea formula. We also illustrate some requirements for IRM-TV-$\ell_1$ to achieve out-of-distribution generalization. Experimental results show that the proposed framework achieves competitive performance in several benchmark machine learning scenarios.

Diagnosing and Rectifying Fake OOD Invariance: A Restructured Causal Approach

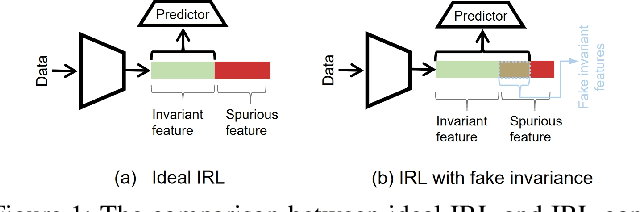
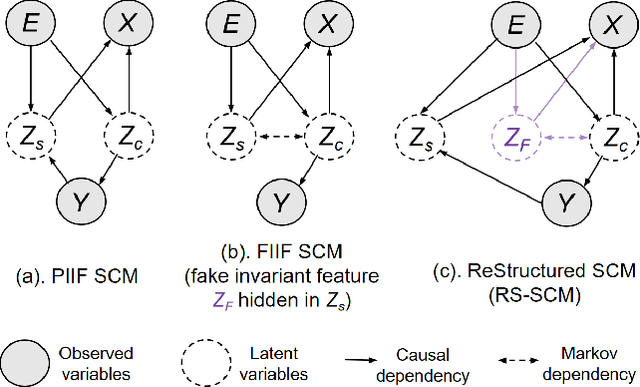
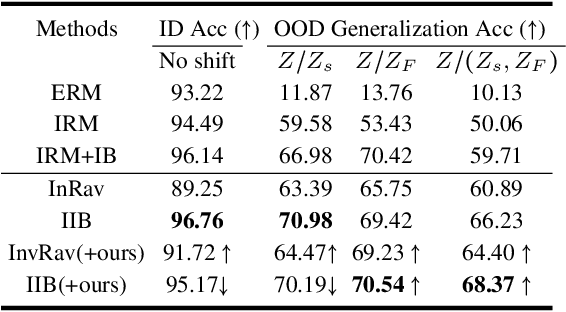
Invariant representation learning (IRL) encourages the prediction from invariant causal features to labels de-confounded from the environments, advancing the technical roadmap of out-of-distribution (OOD) generalization. Despite spotlights around, recent theoretical results verified that some causal features recovered by IRLs merely pretend domain-invariantly in the training environments but fail in unseen domains. The \emph{fake invariance} severely endangers OOD generalization since the trustful objective can not be diagnosed and existing causal surgeries are invalid to rectify. In this paper, we review a IRL family (InvRat) under the Partially and Fully Informative Invariant Feature Structural Causal Models (PIIF SCM /FIIF SCM) respectively, to certify their weaknesses in representing fake invariant features, then, unify their causal diagrams to propose ReStructured SCM (RS-SCM). RS-SCM can ideally rebuild the spurious and the fake invariant features simultaneously. Given this, we further develop an approach based on conditional mutual information with respect to RS-SCM, then rigorously rectify the spurious and fake invariant effects. It can be easily implemented by a small feature selection subnet introduced in the IRL family, which is alternatively optimized to achieve our goal. Experiments verified the superiority of our approach to fight against the fake invariant issue across a variety of OOD generalization benchmarks.

An Investigation of Darwiche and Pearl's Postulates for Iterated Belief Update

Belief revision and update, two significant types of belief change, both focus on how an agent modify her beliefs in presence of new information. The most striking difference between them is that the former studies the change of beliefs in a static world while the latter concentrates on a dynamically-changing world. The famous AGM and KM postulates were proposed to capture rational belief revision and update, respectively. However, both of them are too permissive to exclude some unreasonable changes in the iteration. In response to this weakness, the DP postulates and its extensions for iterated belief revision were presented. Furthermore, Rodrigues integrated these postulates in belief update. Unfortunately, his approach does not meet the basic requirement of iterated belief update. This paper is intended to solve this problem of Rodrigues's approach. Firstly, we present a modification of the original KM postulates based on belief states. Subsequently, we migrate several well-known postulates for iterated belief revision to iterated belief update. Moreover, we provide the exact semantic characterizations based on partial preorders for each of the proposed postulates. Finally, we analyze the compatibility between the above iterated postulates and the KM postulates for belief update.