Invariant Risk Minimization Is A Total Variation Model

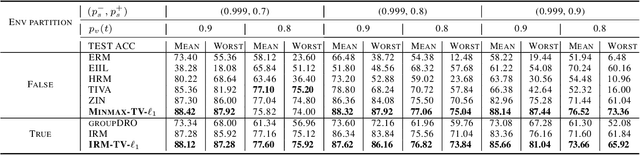
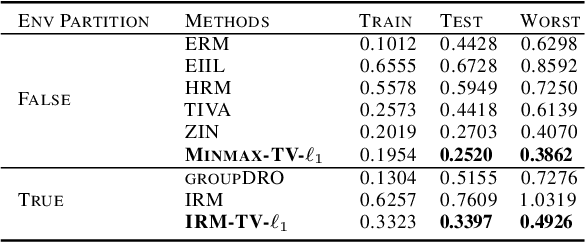
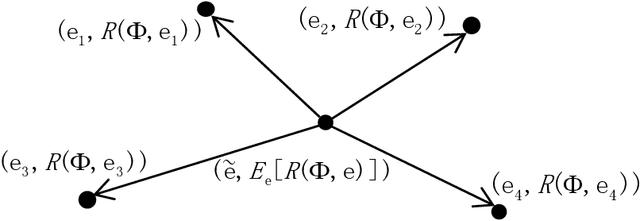
Invariant risk minimization (IRM) is an arising approach to generalize invariant features to different environments in machine learning. While most related works focus on new IRM settings or new application scenarios, the mathematical essence of IRM remains to be properly explained. We verify that IRM is essentially a total variation based on $L^2$ norm (TV-$\ell_2$) of the learning risk with respect to the classifier variable. Moreover, we propose a novel IRM framework based on the TV-$\ell_1$ model. It not only expands the classes of functions that can be used as the learning risk, but also has robust performance in denoising and invariant feature preservation based on the coarea formula. We also illustrate some requirements for IRM-TV-$\ell_1$ to achieve out-of-distribution generalization. Experimental results show that the proposed framework achieves competitive performance in several benchmark machine learning scenarios.