A De-singularity Subgradient Approach for the Extended Weber Location Problem

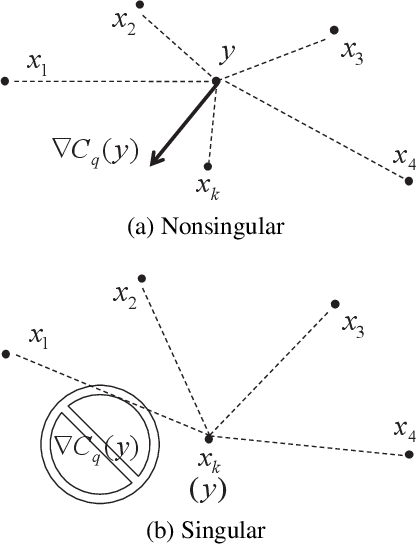
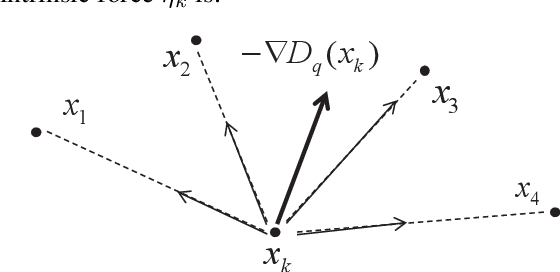
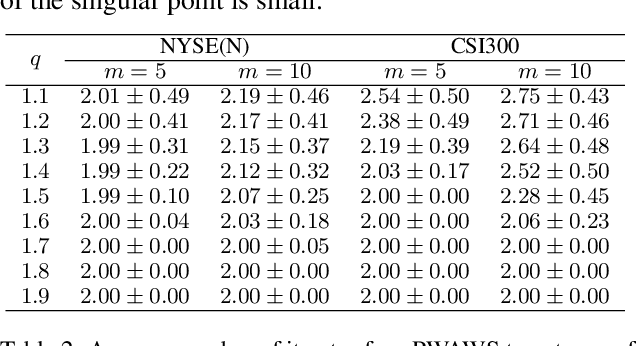
The extended Weber location problem is a classical optimization problem that has inspired some new works in several machine learning scenarios recently. However, most existing algorithms may get stuck due to the singularity at the data points when the power of the cost function $1\leqslant q<2$, such as the widely-used iterative Weiszfeld approach. In this paper, we establish a de-singularity subgradient approach for this problem. We also provide a complete proof of convergence which has fixed some incomplete statements of the proofs for some previous Weiszfeld algorithms. Moreover, we deduce a new theoretical result of superlinear convergence for the iteration sequence in a special case where the minimum point is a singular point. We conduct extensive experiments in a real-world machine learning scenario to show that the proposed approach solves the singularity problem, produces the same results as in the non-singularity cases, and shows a reasonable rate of linear convergence. The results also indicate that the $q$-th power case ($1<q<2$) is more advantageous than the $1$-st power case and the $2$-nd power case in some situations. Hence the de-singularity subgradient approach is beneficial to advancing both theory and practice for the extended Weber location problem.