Feature Subset Weighting for Distance-based Supervised Learning through Choquet Integration

This paper introduces feature subset weighting using monotone measures for distance-based supervised learning. The Choquet integral is used to define a distance metric that incorporates these weights. This integration enables the proposed distances to effectively capture non-linear relationships and account for interactions both between conditional and decision attributes and among conditional attributes themselves, resulting in a more flexible distance measure. In particular, we show how this approach ensures that the distances remain unaffected by the addition of duplicate and strongly correlated features. Another key point of this approach is that it makes feature subset weighting computationally feasible, since only $m$ feature subset weights should be calculated each time instead of calculating all feature subset weights ($2^m$), where $m$ is the number of attributes. Next, we also examine how the use of the Choquet integral for measuring similarity leads to a non-equivalent definition of distance. The relationship between distance and similarity is further explored through dual measures. Additionally, symmetric Choquet distances and similarities are proposed, preserving the classical symmetry between similarity and distance. Finally, we introduce a concrete feature subset weighting distance, evaluate its performance in a $k$-nearest neighbors (KNN) classification setting, and compare it against Mahalanobis distances and weighted distance methods.

Unifying Attribution-Based Explanations Using Functional Decomposition

The black box problem in machine learning has led to the introduction of an ever-increasing set of explanation methods for complex models. These explanations have different properties, which in turn has led to the problem of method selection: which explanation method is most suitable for a given use case? In this work, we propose a unifying framework of attribution-based explanation methods, which provides a step towards a rigorous study of the similarities and differences of explanations. We first introduce removal-based attribution methods (RBAMs), and show that an extensively broad selection of existing methods can be viewed as such RBAMs. We then introduce the canonical additive decomposition (CAD). This is a general construction for additively decomposing any function based on the central idea of removing (groups of) features. We proceed to show that indeed every valid additive decomposition is an instance of the CAD, and that any removal-based attribution method is associated with a specific CAD. Next, we show that any removal-based attribution method can be completely defined as a game-theoretic value or interaction index for a specific (possibly constant-shifted) cooperative game, which is defined using the corresponding CAD of the method. We then use this intrinsic connection to define formal descriptions of specific behaviours of explanation methods, which we also call functional axioms, and identify sufficient conditions on the corresponding CAD and game-theoretic value or interaction index of an attribution method under which the attribution method is guaranteed to adhere to these functional axioms. Finally, we show how this unifying framework can be used to develop new, efficient approximations for existing explanation methods.

Pattern or Artifact? Interactively Exploring Embedding Quality with TRACE

This paper presents TRACE, a tool to analyze the quality of 2D embeddings generated through dimensionality reduction techniques. Dimensionality reduction methods often prioritize preserving either local neighborhoods or global distances, but insights from visual structures can be misleading if the objective has not been achieved uniformly. TRACE addresses this challenge by providing a scalable and extensible pipeline for computing both local and global quality measures. The interactive browser-based interface allows users to explore various embeddings while visually assessing the pointwise embedding quality. The interface also facilitates in-depth analysis by highlighting high-dimensional nearest neighbors for any group of points and displaying high-dimensional distances between points. TRACE enables analysts to make informed decisions regarding the most suitable dimensionality reduction method for their specific use case, by showing the degree and location where structure is preserved in the reduced space.

GroupEnc: encoder with group loss for global structure preservation

Recent advances in dimensionality reduction have achieved more accurate lower-dimensional embeddings of high-dimensional data. In addition to visualisation purposes, these embeddings can be used for downstream processing, including batch effect normalisation, clustering, community detection or trajectory inference. We use the notion of structure preservation at both local and global levels to create a deep learning model, based on a variational autoencoder (VAE) and the stochastic quartet loss from the SQuadMDS algorithm. Our encoder model, called GroupEnc, uses a 'group loss' function to create embeddings with less global structure distortion than VAEs do, while keeping the model parametric and the architecture flexible. We validate our approach using publicly available biological single-cell transcriptomic datasets, employing RNX curves for evaluation.

Topologically Regularized Data Embeddings

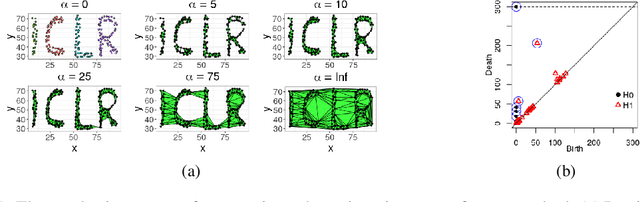
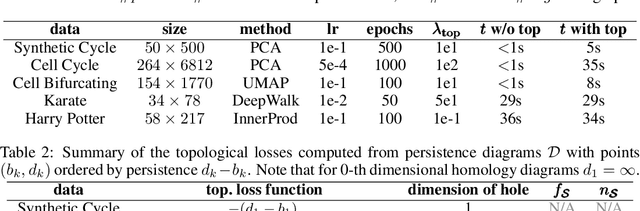
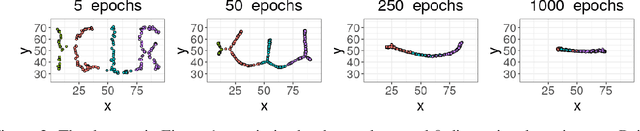
Unsupervised representation learning methods are widely used for gaining insight into high-dimensional, unstructured, or structured data. In some cases, users may have prior topological knowledge about the data, such as a known cluster structure or the fact that the data is known to lie along a tree- or graph-structured topology. However, generic methods to ensure such structure is salient in the low-dimensional representations are lacking. This negatively impacts the interpretability of low-dimensional embeddings, and plausibly downstream learning tasks. To address this issue, we introduce topological regularization: a generic approach based on algebraic topology to incorporate topological prior knowledge into low-dimensional embeddings. We introduce a class of topological loss functions, and show that jointly optimizing an embedding loss with such a topological loss function as a regularizer yields embeddings that reflect not only local proximities but also the desired topological structure. We include a self-contained overview of the required foundational concepts in algebraic topology, and provide intuitive guidance on how to design topological loss functions for a variety of shapes, such as clusters, cycles, and bifurcations. We empirically evaluate the proposed approach on computational efficiency, robustness, and versatility in combination with linear and non-linear dimensionality reduction and graph embedding methods.

Distilling Deep RL Models Into Interpretable Neuro-Fuzzy Systems

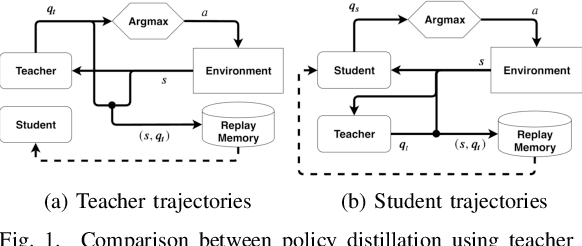
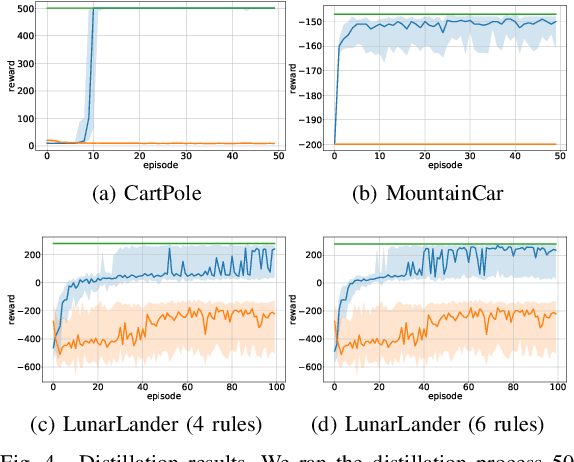
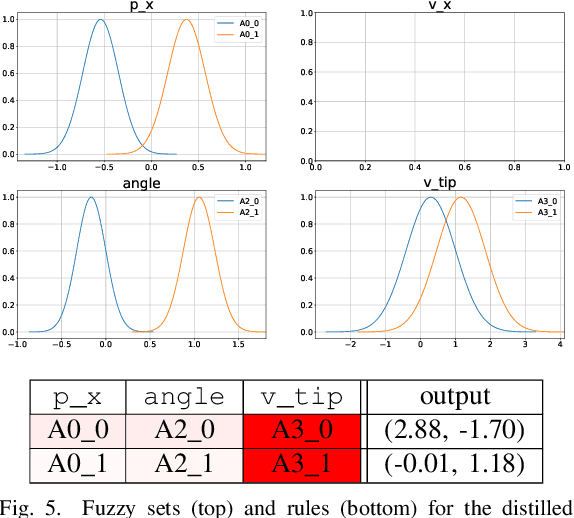
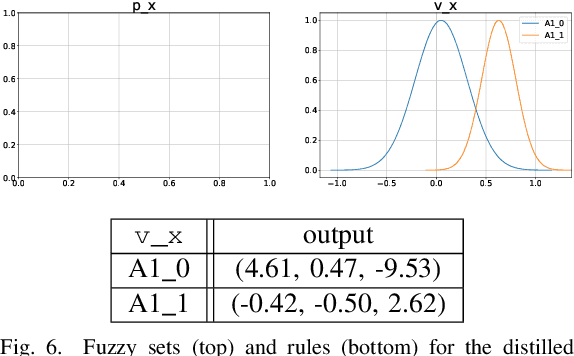
Deep Reinforcement Learning uses a deep neural network to encode a policy, which achieves very good performance in a wide range of applications but is widely regarded as a black box model. A more interpretable alternative to deep networks is given by neuro-fuzzy controllers. Unfortunately, neuro-fuzzy controllers often need a large number of rules to solve relatively simple tasks, making them difficult to interpret. In this work, we present an algorithm to distill the policy from a deep Q-network into a compact neuro-fuzzy controller. This allows us to train compact neuro-fuzzy controllers through distillation to solve tasks that they are unable to solve directly, combining the flexibility of deep reinforcement learning and the interpretability of compact rule bases. We demonstrate the algorithm on three well-known environments from OpenAI Gym, where we nearly match the performance of a DQN agent using only 2 to 6 fuzzy rules.

PDD-SHAP: Fast Approximations for Shapley Values using Functional Decomposition

Because of their strong theoretical properties, Shapley values have become very popular as a way to explain predictions made by black box models. Unfortuately, most existing techniques to compute Shapley values are computationally very expensive. We propose PDD-SHAP, an algorithm that uses an ANOVA-based functional decomposition model to approximate the black-box model being explained. This allows us to calculate Shapley values orders of magnitude faster than existing methods for large datasets, significantly reducing the amortized cost of computing Shapley values when many predictions need to be explained.

Evaluating Feature Attribution Methods in the Image Domain

Feature attribution maps are a popular approach to highlight the most important pixels in an image for a given prediction of a model. Despite a recent growth in popularity and available methods, little attention is given to the objective evaluation of such attribution maps. Building on previous work in this domain, we investigate existing metrics and propose new variants of metrics for the evaluation of attribution maps. We confirm a recent finding that different attribution metrics seem to measure different underlying concepts of attribution maps, and extend this finding to a larger selection of attribution metrics. We also find that metric results on one dataset do not necessarily generalize to other datasets, and methods with desirable theoretical properties such as DeepSHAP do not necessarily outperform computationally cheaper alternatives. Based on these findings, we propose a general benchmarking approach to identify the ideal feature attribution method for a given use case. Implementations of attribution metrics and our experiments are available online.

The Curse Revisited: a Newly Quantified Concept of Meaningful Distances for Learning from High-Dimensional Noisy Data

Distances between data points are widely used in point cloud representation learning. Yet, it is no secret that under the effect of noise, these distances-and thus the models based upon them-may lose their usefulness in high dimensions. Indeed, the small marginal effects of the noise may then accumulate quickly, shifting empirical closest and furthest neighbors away from the ground truth. In this paper, we characterize such effects in high-dimensional data using an asymptotic probabilistic expression. Furthermore, while it has been previously argued that neighborhood queries become meaningless and unstable when there is a poor relative discrimination between the furthest and closest point, we conclude that this is not necessarily the case when explicitly separating the ground truth data from the noise. More specifically, we derive that under particular conditions, empirical neighborhood relations affected by noise are still likely to be true even when we observe this discrimination to be poor. We include thorough empirical verification of our results, as well as experiments that interestingly show our derived phase shift where neighbors become random or not is identical to the phase shift where common dimensionality reduction methods perform poorly or well for finding low-dimensional representations of high-dimensional data with dense noise.