Fuzzy Rough Choquet Distances for Classification

This paper introduces a novel Choquet distance using fuzzy rough set based measures. The proposed distance measure combines the attribute information received from fuzzy rough set theory with the flexibility of the Choquet integral. This approach is designed to adeptly capture non-linear relationships within the data, acknowledging the interplay of the conditional attributes towards the decision attribute and resulting in a more flexible and accurate distance. We explore its application in the context of machine learning, with a specific emphasis on distance-based classification approaches (e.g. k-nearest neighbours). The paper examines two fuzzy rough set based measures that are based on the positive region. Moreover, we explore two procedures for monotonizing the measures derived from fuzzy rough set theory, making them suitable for use with the Choquet integral, and investigate their differences.

FRRI: a novel algorithm for fuzzy-rough rule induction

Interpretability is the next frontier in machine learning research. In the search for white box models - as opposed to black box models, like random forests or neural networks - rule induction algorithms are a logical and promising option, since the rules can easily be understood by humans. Fuzzy and rough set theory have been successfully applied to this archetype, almost always separately. As both approaches to rule induction involve granular computing based on the concept of equivalence classes, it is natural to combine them. The QuickRules\cite{JensenCornelis2009} algorithm was a first attempt at using fuzzy rough set theory for rule induction. It is based on QuickReduct, a greedy algorithm for building decision reducts. QuickRules already showed an improvement over other rule induction methods. However, to evaluate the full potential of a fuzzy rough rule induction algorithm, one needs to start from the foundations. In this paper, we introduce a novel rule induction algorithm called Fuzzy Rough Rule Induction (FRRI). We provide background and explain the workings of our algorithm. Furthermore, we perform a computational experiment to evaluate the performance of our algorithm and compare it to other state-of-the-art rule induction approaches. We find that our algorithm is more accurate while creating small rulesets consisting of relatively short rules. We end the paper by outlining some directions for future work.

On the Granular Representation of Fuzzy Quantifier-Based Fuzzy Rough Sets

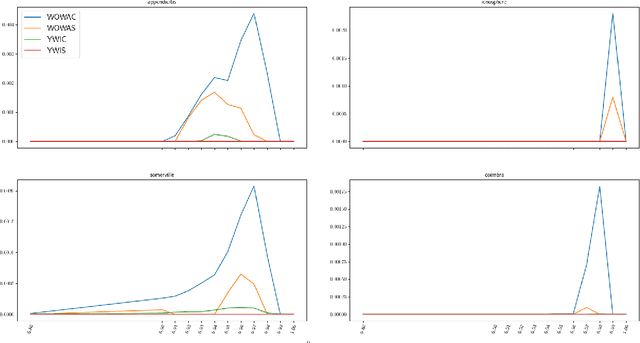
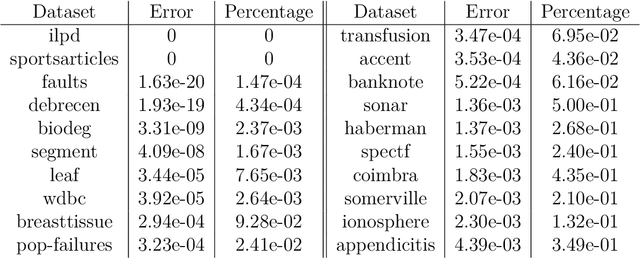
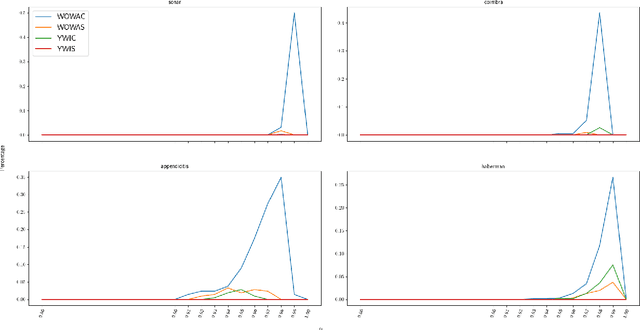
Rough set theory is a well-known mathematical framework that can deal with inconsistent data by providing lower and upper approximations of concepts. A prominent property of these approximations is their granular representation: that is, they can be written as unions of simple sets, called granules. The latter can be identified with "if. . . , then. . . " rules, which form the backbone of rough set rule induction. It has been shown previously that this property can be maintained for various fuzzy rough set models, including those based on ordered weighted average (OWA) operators. In this paper, we will focus on some instances of the general class of fuzzy quantifier-based fuzzy rough sets (FQFRS). In these models, the lower and upper approximations are evaluated using binary and unary fuzzy quantifiers, respectively. One of the main targets of this study is to examine the granular representation of different models of FQFRS. The main findings reveal that Choquet-based fuzzy rough sets can be represented granularly under the same conditions as OWA-based fuzzy rough sets, whereas Sugeno-based FRS can always be represented granularly. This observation highlights the potential of these models for resolving data inconsistencies and managing noise.

A unified weighting framework for evaluating nearest neighbour classification

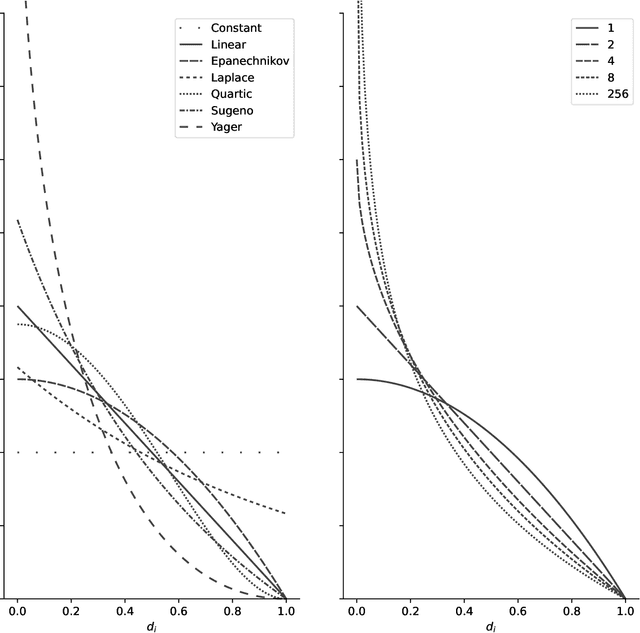
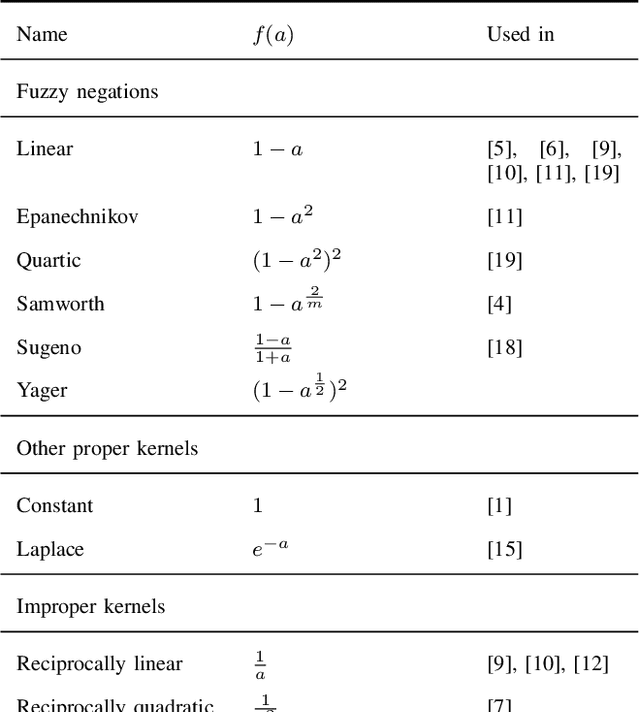
We present the first comprehensive and large-scale evaluation of classical (NN), fuzzy (FNN) and fuzzy rough (FRNN) nearest neighbour classification. We show that existing proposals for nearest neighbour weighting can be standardised in the form of kernel functions, applied to the distance values and/or ranks of the nearest neighbours of a test instance. Furthermore, we identify three commonly used distance functions and four scaling measures. We systematically evaluate these choices on a collection of 85 real-life classification datasets. We find that NN, FNN and FRNN all perform best with Boscovich distance. NN and FRNN perform best with a combination of Samworth rank- and distance weights and scaling by the mean absolute deviation around the median ($r_1$), the standard deviaton ($r_2$) or the interquartile range ($r_{\infty}^*$), while FNN performs best with only Samworth distance-weights and $r_1$- or $r_2$-scaling. We also introduce a new kernel based on fuzzy Yager negation, and show that NN achieves comparable performance with Yager distance-weights, which are simpler to implement than a combination of Samworth distance- and rank-weights. Finally, we demonstrate that FRNN generally outperforms NN, which in turns performs systematically better than FNN.

Classifying token frequencies using angular Minkowski $p$-distance

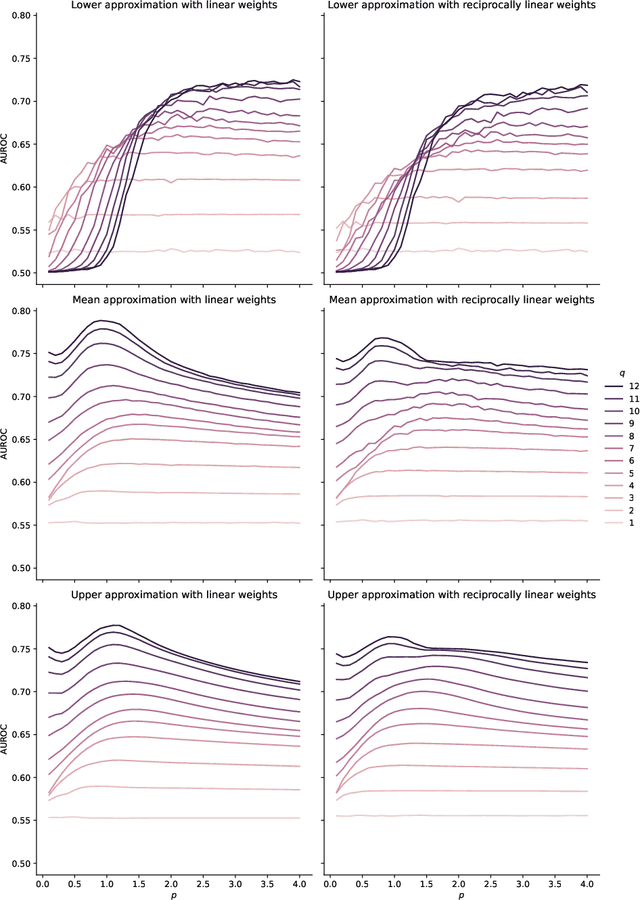
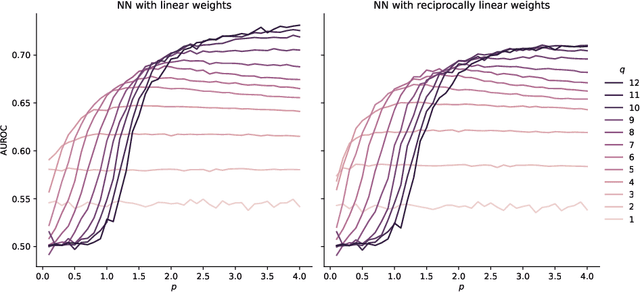
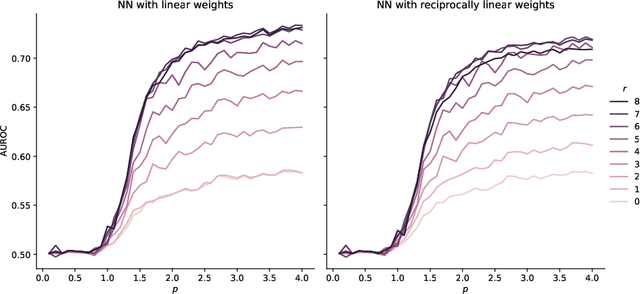
Angular Minkowski $p$-distance is a dissimilarity measure that is obtained by replacing Euclidean distance in the definition of cosine dissimilarity with other Minkowski $p$-distances. Cosine dissimilarity is frequently used with datasets containing token frequencies, and angular Minkowski $p$-distance may potentially be an even better choice for certain tasks. In a case study based on the 20-newsgroups dataset, we evaluate clasification performance for classical weighted nearest neighbours, as well as fuzzy rough nearest neighbours. In addition, we analyse the relationship between the hyperparameter $p$, the dimensionality $m$ of the dataset, the number of neighbours $k$, the choice of weights and the choice of classifier. We conclude that it is possible to obtain substantially higher classification performance with angular Minkowski $p$-distance with suitable values for $p$ than with classical cosine dissimilarity.

Fuzzy Rough Sets Based on Fuzzy Quantification

One of the weaknesses of classical (fuzzy) rough sets is their sensitivity to noise, which is particularly undesirable for machine learning applications. One approach to solve this issue is by making use of fuzzy quantifiers, as done by the vaguely quantified fuzzy rough set (VQFRS) model. While this idea is intuitive, the VQFRS model suffers from both theoretical flaws as well as from suboptimal performance in applications. In this paper, we improve on VQFRS by introducing fuzzy quantifier-based fuzzy rough sets (FQFRS), an intuitive generalization of fuzzy rough sets that makes use of general unary and binary quantification models. We show how several existing models fit in this generalization as well as how it inspires novel ones. Several binary quantification models are proposed to be used with FQFRS. We conduct a theoretical study of their properties, and investigate their potential by applying them to classification problems. In particular, we highlight Yager's Weighted Implication-based (YWI) binary quantification model, which induces a fuzzy rough set model that is both a significant improvement on VQFRS, as well as a worthy competitor to the popular ordered weighted averaging based fuzzy rough set (OWAFRS) model.

Evaluation of the impact of the indiscernibility relation on the fuzzy-rough nearest neighbours algorithm

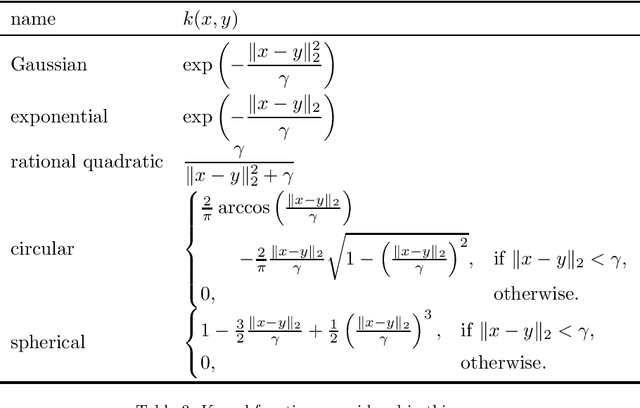
Fuzzy rough sets are well-suited for working with vague, imprecise or uncertain information and have been succesfully applied in real-world classification problems. One of the prominent representatives of this theory is fuzzy-rough nearest neighbours (FRNN), a classification algorithm based on the classical k-nearest neighbours algorithm. The crux of FRNN is the indiscernibility relation, which measures how similar two elements in the data set of interest are. In this paper, we investigate the impact of this indiscernibility relation on the performance of FRNN classification. In addition to relations based on distance functions and kernels, we also explore the effect of distance metric learning on FRNN for the first time. Furthermore, we also introduce an asymmetric, class-specific relation based on the Mahalanobis distance which uses the correlation within each class, and which shows a significant improvement over the regular Mahalanobis distance, but is still beaten by the Manhattan distance. Overall, the Neighbourhood Components Analysis algorithm is found to be the best performer, trading speed for accuracy.

Representing missing values through polar encoding

We propose polar encoding, a representation of categorical and numerical $[0,1]$-valued attributes with missing values that preserves the information encoded in the distribution of the missing values. Unlike the existing missing-indicator approach, this does not require imputation. We support our proposal with three different arguments. Firstly, polar encoding ensures that missing values become equidistant from all non-missing values by mapping the latter onto the unit circle. Secondly, polar encoding lets decision trees choose how missing values should be split, providing a practical realisation of the missingness incorporated in attributes (MIA) proposal. And lastly, polar encoding corresponds to the normalised representation of categorical and $[0,1]$-valued attributes when viewed as barycentric attributes, a new concept based on traditional barycentric coordinates. In particular, we show that barycentric attributes are fuzzified categorical attributes, that their normalised representation generalises one-hot encoding, and that the polar encoding of $[0, 1]$-valued attributes is analogous to the one-hot encoding of binary attributes. With an experiment based on twenty real-life datasets with missing values, we show that polar encoding performs about as well or better than the missing-indicator approach in terms of the resulting classification performance.

No imputation without representation

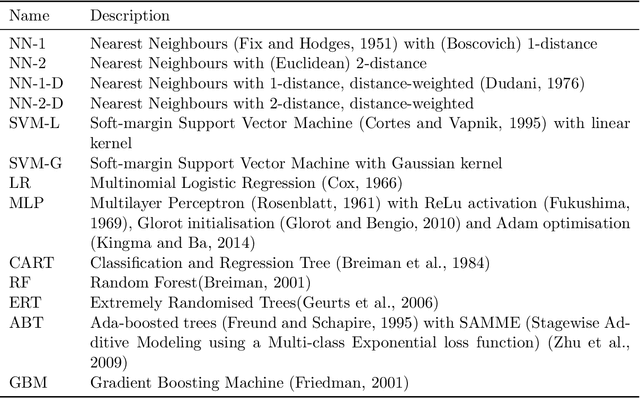
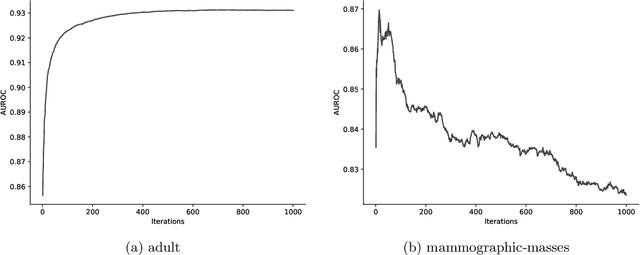
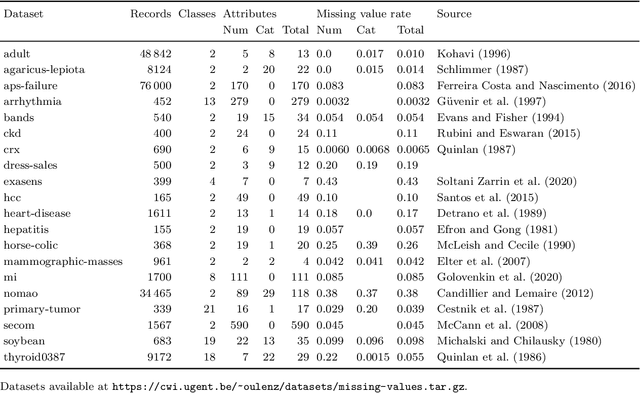
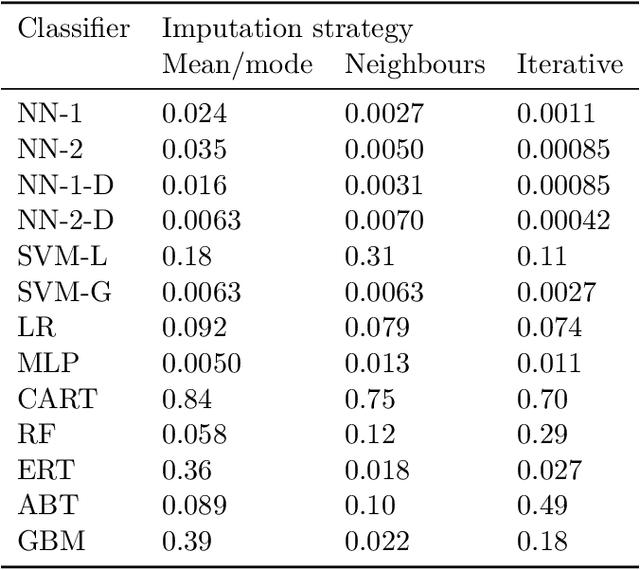
By filling in missing values in datasets, imputation allows these datasets to be used with algorithms that cannot handle missing values by themselves. However, missing values may in principle contribute useful information that is lost through imputation. The missing-indicator approach can be used in combination with imputation to instead represent this information as a part of the dataset. There are several theoretical considerations why missing-indicators may or may not be beneficial, but there has not been any large-scale practical experiment on real-life datasets to test this question for machine learning predictions. We perform this experiment for three imputation strategies and a range of different classification algorithms, on the basis of twenty real-life datasets. We find that on these datasets, missing-indicators generally increase classification performance. In addition, we find no evidence for most algorithms that nearest neighbour and iterative imputation lead to better performance than simple mean/mode imputation. Therefore, we recommend the use of missing-indicators with mean/mode imputation as a safe default, with the caveat that for decision trees, pruning is necessary to prevent overfitting. In a follow-up experiment, we determine attribute-specific missingness thresholds for each classifier above which missing-indicators are more likely than not to increase classification performance, and observe that these thresholds are much lower for categorical than for numerical attributes. Finally, we argue that mean imputation of numerical attributes may preserve some of the information from missing values, and we show that in the absence of missing-indicators, it can similarly be useful to apply mean imputation to one-hot encoded categorical attributes instead of mode imputation.

Fuzzy granular approximation classifier

In this article, a new Fuzzy Granular Approximation Classifier (FGAC) is introduced. The classifier is based on the previously introduced concept of the granular approximation and its multi-class classification case. The classifier is instance-based and its biggest advantage is its local transparency i.e., the ability to explain every individual prediction it makes. We first develop the FGAC for the binary classification case and the multi-class classification case and we discuss its variation that includes the Ordered Weighted Average (OWA) operators. Those variations of the FGAC are then empirically compared with other locally transparent ML methods. At the end, we discuss the transparency of the FGAC and its advantage over other locally transparent methods. We conclude that while the FGAC has similar predictive performance to other locally transparent ML models, its transparency can be superior in certain cases.