Directional anomaly detection

Semi-supervised anomaly detection is based on the principle that potential anomalies are those records that look different from normal training data. However, in some cases we are specifically interested in anomalies that correspond to high attribute values (or low, but not both). We present two asymmetrical distance measures that take this directionality into account: ramp distance and signed distance. Through experiments on synthetic and real-life datasets we show that ramp distance performs as well or better than the absolute distance traditionally used in anomaly detection. While signed distance also performs well on synthetic data, it performs substantially poorer on real-life datasets. We argue that this reflects the fact that in practice, good scores on some attributes should not be allowed to compensate for bad scores on others.

A unified weighting framework for evaluating nearest neighbour classification

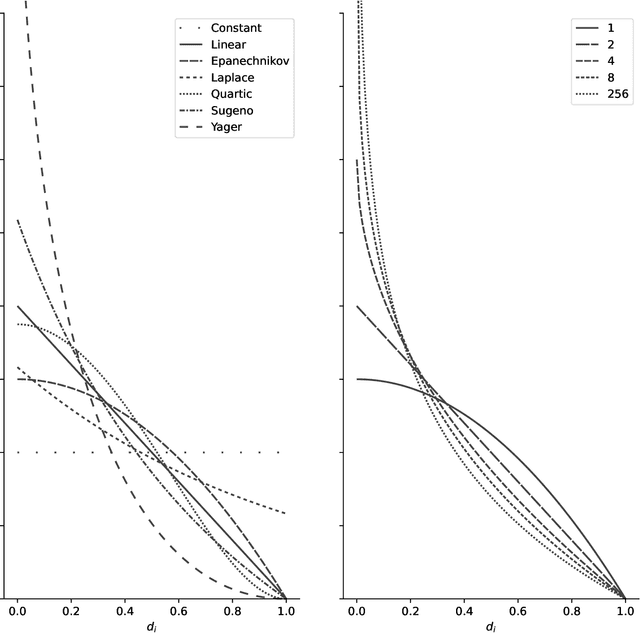
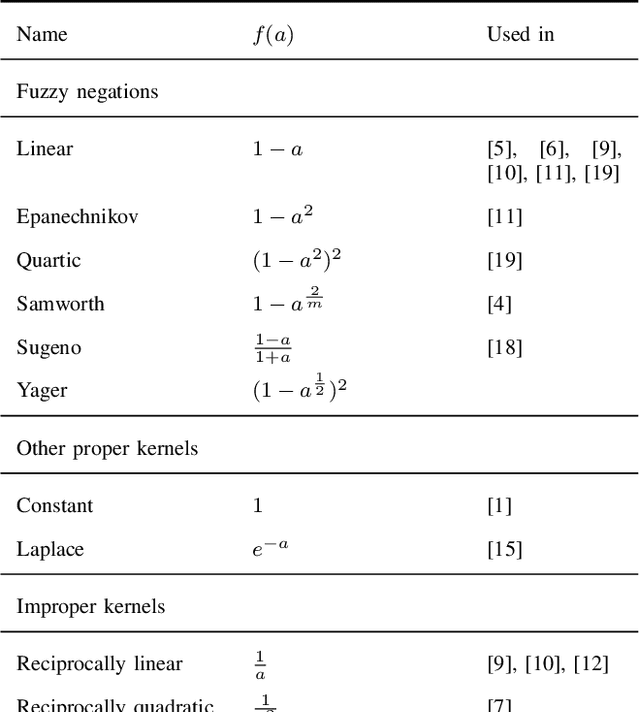
We present the first comprehensive and large-scale evaluation of classical (NN), fuzzy (FNN) and fuzzy rough (FRNN) nearest neighbour classification. We show that existing proposals for nearest neighbour weighting can be standardised in the form of kernel functions, applied to the distance values and/or ranks of the nearest neighbours of a test instance. Furthermore, we identify three commonly used distance functions and four scaling measures. We systematically evaluate these choices on a collection of 85 real-life classification datasets. We find that NN, FNN and FRNN all perform best with Boscovich distance. NN and FRNN perform best with a combination of Samworth rank- and distance weights and scaling by the mean absolute deviation around the median ($r_1$), the standard deviaton ($r_2$) or the interquartile range ($r_{\infty}^*$), while FNN performs best with only Samworth distance-weights and $r_1$- or $r_2$-scaling. We also introduce a new kernel based on fuzzy Yager negation, and show that NN achieves comparable performance with Yager distance-weights, which are simpler to implement than a combination of Samworth distance- and rank-weights. Finally, we demonstrate that FRNN generally outperforms NN, which in turns performs systematically better than FNN.

Classifying token frequencies using angular Minkowski $p$-distance

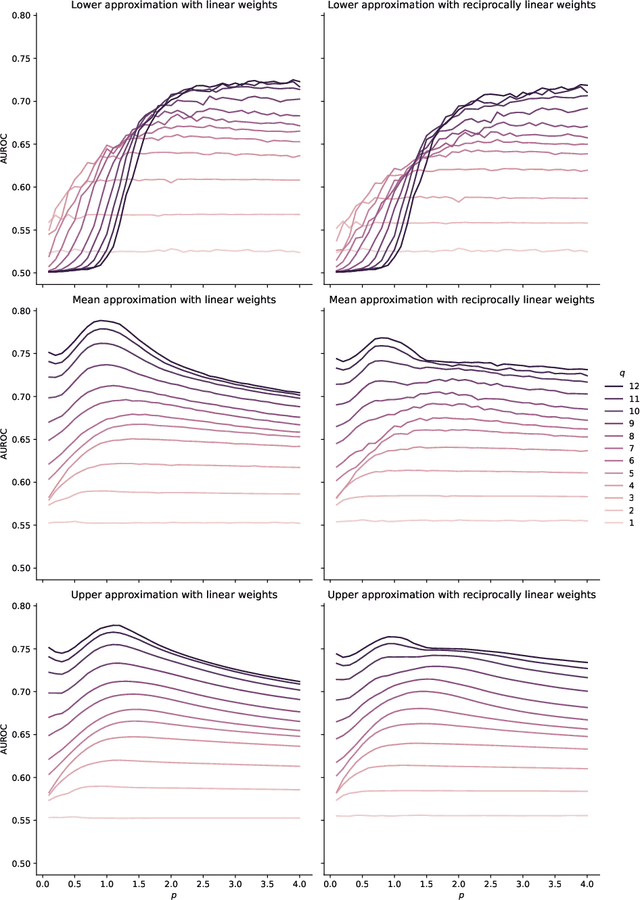
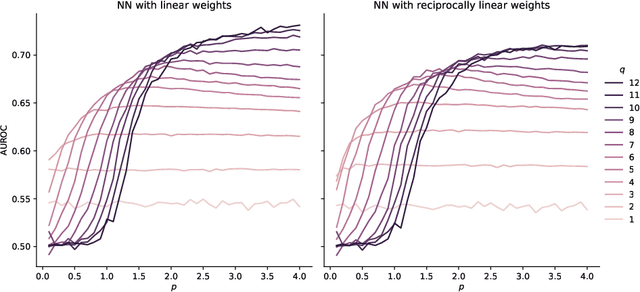
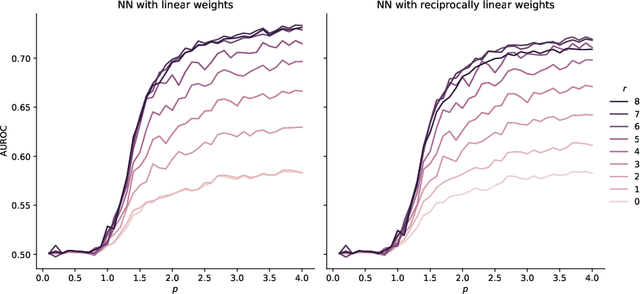
Angular Minkowski $p$-distance is a dissimilarity measure that is obtained by replacing Euclidean distance in the definition of cosine dissimilarity with other Minkowski $p$-distances. Cosine dissimilarity is frequently used with datasets containing token frequencies, and angular Minkowski $p$-distance may potentially be an even better choice for certain tasks. In a case study based on the 20-newsgroups dataset, we evaluate clasification performance for classical weighted nearest neighbours, as well as fuzzy rough nearest neighbours. In addition, we analyse the relationship between the hyperparameter $p$, the dimensionality $m$ of the dataset, the number of neighbours $k$, the choice of weights and the choice of classifier. We conclude that it is possible to obtain substantially higher classification performance with angular Minkowski $p$-distance with suitable values for $p$ than with classical cosine dissimilarity.

Representing missing values through polar encoding

We propose polar encoding, a representation of categorical and numerical $[0,1]$-valued attributes with missing values that preserves the information encoded in the distribution of the missing values. Unlike the existing missing-indicator approach, this does not require imputation. We support our proposal with three different arguments. Firstly, polar encoding ensures that missing values become equidistant from all non-missing values by mapping the latter onto the unit circle. Secondly, polar encoding lets decision trees choose how missing values should be split, providing a practical realisation of the missingness incorporated in attributes (MIA) proposal. And lastly, polar encoding corresponds to the normalised representation of categorical and $[0,1]$-valued attributes when viewed as barycentric attributes, a new concept based on traditional barycentric coordinates. In particular, we show that barycentric attributes are fuzzified categorical attributes, that their normalised representation generalises one-hot encoding, and that the polar encoding of $[0, 1]$-valued attributes is analogous to the one-hot encoding of binary attributes. With an experiment based on twenty real-life datasets with missing values, we show that polar encoding performs about as well or better than the missing-indicator approach in terms of the resulting classification performance.

No imputation without representation

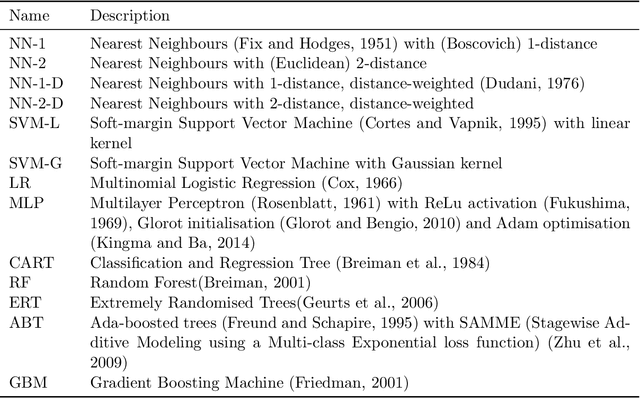
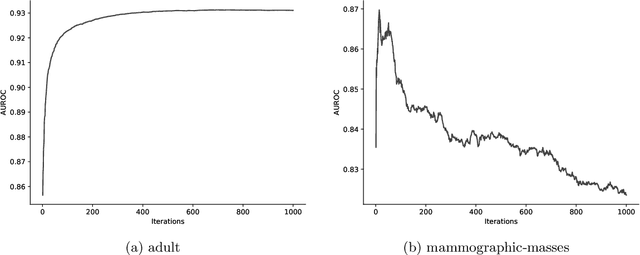
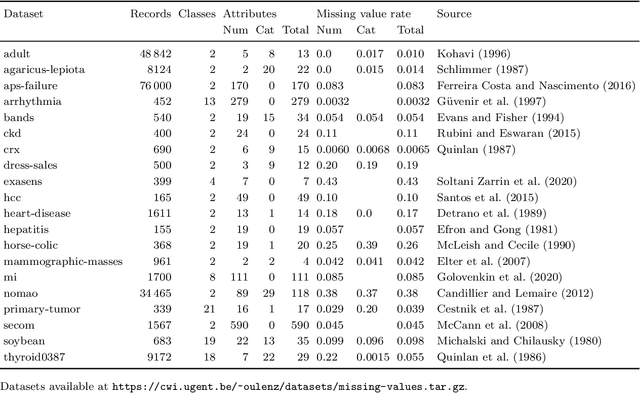
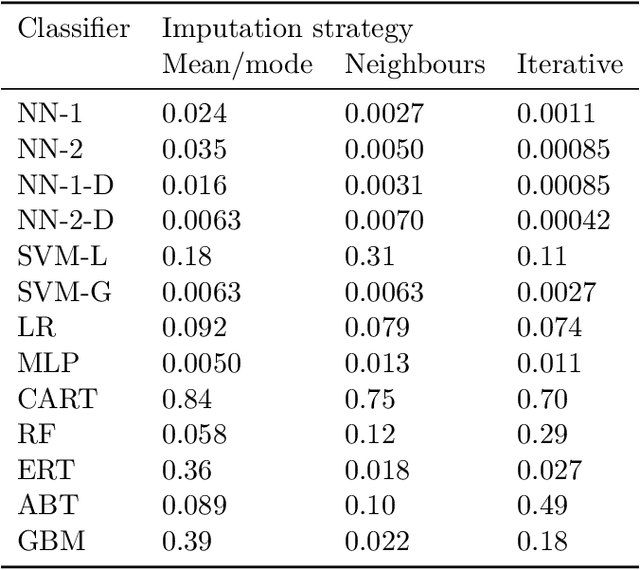
By filling in missing values in datasets, imputation allows these datasets to be used with algorithms that cannot handle missing values by themselves. However, missing values may in principle contribute useful information that is lost through imputation. The missing-indicator approach can be used in combination with imputation to instead represent this information as a part of the dataset. There are several theoretical considerations why missing-indicators may or may not be beneficial, but there has not been any large-scale practical experiment on real-life datasets to test this question for machine learning predictions. We perform this experiment for three imputation strategies and a range of different classification algorithms, on the basis of twenty real-life datasets. We find that on these datasets, missing-indicators generally increase classification performance. In addition, we find no evidence for most algorithms that nearest neighbour and iterative imputation lead to better performance than simple mean/mode imputation. Therefore, we recommend the use of missing-indicators with mean/mode imputation as a safe default, with the caveat that for decision trees, pruning is necessary to prevent overfitting. In a follow-up experiment, we determine attribute-specific missingness thresholds for each classifier above which missing-indicators are more likely than not to increase classification performance, and observe that these thresholds are much lower for categorical than for numerical attributes. Finally, we argue that mean imputation of numerical attributes may preserve some of the information from missing values, and we show that in the absence of missing-indicators, it can similarly be useful to apply mean imputation to one-hot encoded categorical attributes instead of mode imputation.

Choquet-Based Fuzzy Rough Sets

Fuzzy rough set theory can be used as a tool for dealing with inconsistent data when there is a gradual notion of indiscernibility between objects. It does this by providing lower and upper approximations of concepts. In classical fuzzy rough sets, the lower and upper approximations are determined using the minimum and maximum operators, respectively. This is undesirable for machine learning applications, since it makes these approximations sensitive to outlying samples. To mitigate this problem, ordered weighted average (OWA) based fuzzy rough sets were introduced. In this paper, we show how the OWA-based approach can be interpreted intuitively in terms of vague quantification, and then generalize it to Choquet-based fuzzy rough sets (CFRS). This generalization maintains desirable theoretical properties, such as duality and monotonicity. Furthermore, it provides more flexibility for machine learning applications. In particular, we show that it enables the seamless integration of outlier detection algorithms, to enhance the robustness of machine learning algorithms based on fuzzy rough sets.

Optimised one-class classification performance

We provide a thorough treatment of hyperparameter optimisation for three data descriptors with a good track-record in the literature: Support Vector Machine (SVM), Nearest Neighbour Distance (NND) and Average Localised Proximity (ALP). The hyperparameters of SVM have to be optimised through cross-validation, while NND and ALP allow the reuse of a single nearest-neighbour query and an efficient form of leave-one-out validation. We experimentally evaluate the effect of hyperparameter optimisation with 246 classification problems drawn from 50 datasets. From a selection of optimisation algorithms, the recent Malherbe-Powell proposal optimises the hyperparameters of all three data descriptors most efficiently. We calculate the increase in test AUROC and the amount of overfitting as a function of the number of hyperparameter evaluations. After 50 evaluations, ALP and SVM both significantly outperform NND. The performance of ALP and SVM is comparable, but ALP can be optimised more efficiently, while a choice between ALP and SVM based on validation AUROC gives the best overall result. This distils the many variables of one-class classification with hyperparameter optimisation down to a clear choice with a known trade-off, allowing practitioners to make informed decisions.

Average Localised Proximity: a new data descriptor with good default one-class classification performance

One-class classification is a challenging subfield of machine learning in which so-called data descriptors are used to predict membership of a class based solely on positive examples of that class, and no counter-examples. A number of data descriptors that have been shown to perform well in previous studies of one-class classification, like the Support Vector Machine (SVM), require setting one or more hyperparameters. There has been no systematic attempt to date to determine optimal default values for these hyperparameters, which limits their ease of use, especially in comparison with hyperparameter-free proposals like the Isolation Forest (IF). We address this issue by determining optimal default hyperparameter values across a collection of 246 one-class classification problems derived from 50 different real-world datasets. In addition, we propose a new data descriptor, Average Localised Proximity (ALP) to address certain issues with existing approaches based on nearest neighbour distances. Finally, we evaluate classification performance using a leave-one-dataset-out procedure, and find strong evidence that ALP outperforms IF and a number of other data descriptors, as well as weak evidence that it outperforms SVM, making ALP a good default choice.