Classifying token frequencies using angular Minkowski $p$-distance
Paper and Code
Sep 25, 2023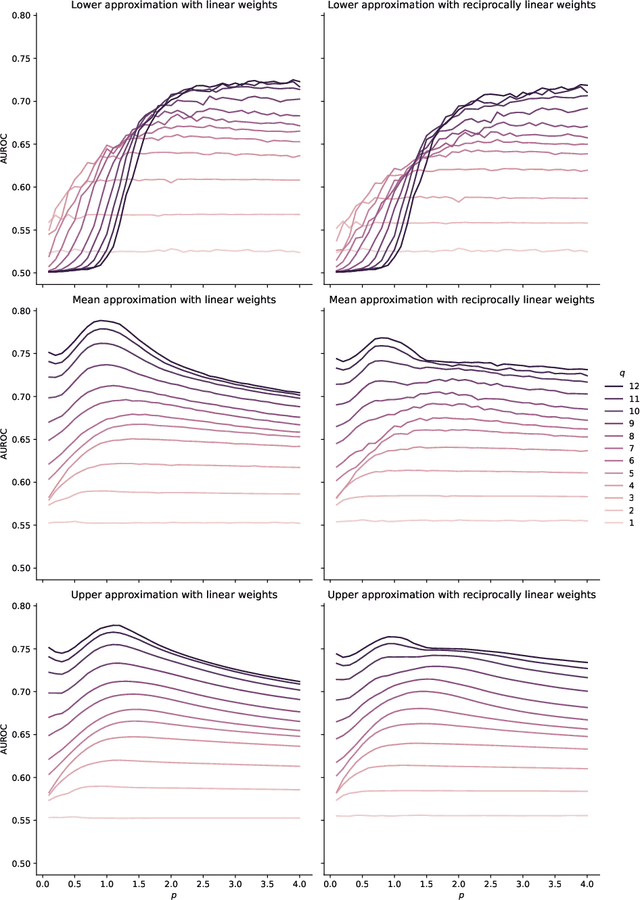

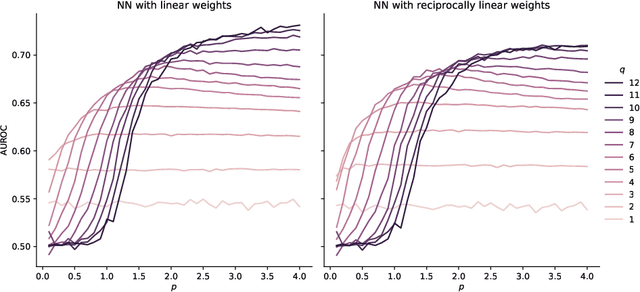
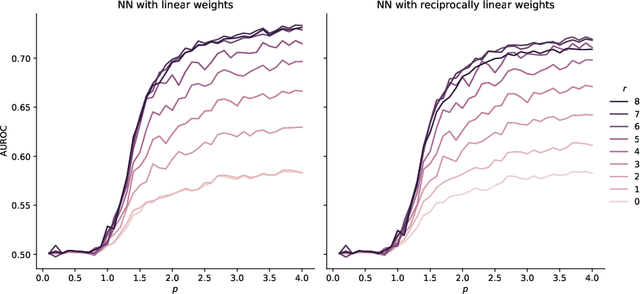
Angular Minkowski $p$-distance is a dissimilarity measure that is obtained by replacing Euclidean distance in the definition of cosine dissimilarity with other Minkowski $p$-distances. Cosine dissimilarity is frequently used with datasets containing token frequencies, and angular Minkowski $p$-distance may potentially be an even better choice for certain tasks. In a case study based on the 20-newsgroups dataset, we evaluate clasification performance for classical weighted nearest neighbours, as well as fuzzy rough nearest neighbours. In addition, we analyse the relationship between the hyperparameter $p$, the dimensionality $m$ of the dataset, the number of neighbours $k$, the choice of weights and the choice of classifier. We conclude that it is possible to obtain substantially higher classification performance with angular Minkowski $p$-distance with suitable values for $p$ than with classical cosine dissimilarity.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge