Feature Subset Weighting for Distance-based Supervised Learning through Choquet Integration

This paper introduces feature subset weighting using monotone measures for distance-based supervised learning. The Choquet integral is used to define a distance metric that incorporates these weights. This integration enables the proposed distances to effectively capture non-linear relationships and account for interactions both between conditional and decision attributes and among conditional attributes themselves, resulting in a more flexible distance measure. In particular, we show how this approach ensures that the distances remain unaffected by the addition of duplicate and strongly correlated features. Another key point of this approach is that it makes feature subset weighting computationally feasible, since only $m$ feature subset weights should be calculated each time instead of calculating all feature subset weights ($2^m$), where $m$ is the number of attributes. Next, we also examine how the use of the Choquet integral for measuring similarity leads to a non-equivalent definition of distance. The relationship between distance and similarity is further explored through dual measures. Additionally, symmetric Choquet distances and similarities are proposed, preserving the classical symmetry between similarity and distance. Finally, we introduce a concrete feature subset weighting distance, evaluate its performance in a $k$-nearest neighbors (KNN) classification setting, and compare it against Mahalanobis distances and weighted distance methods.

Fuzzy Rough Choquet Distances for Classification

This paper introduces a novel Choquet distance using fuzzy rough set based measures. The proposed distance measure combines the attribute information received from fuzzy rough set theory with the flexibility of the Choquet integral. This approach is designed to adeptly capture non-linear relationships within the data, acknowledging the interplay of the conditional attributes towards the decision attribute and resulting in a more flexible and accurate distance. We explore its application in the context of machine learning, with a specific emphasis on distance-based classification approaches (e.g. k-nearest neighbours). The paper examines two fuzzy rough set based measures that are based on the positive region. Moreover, we explore two procedures for monotonizing the measures derived from fuzzy rough set theory, making them suitable for use with the Choquet integral, and investigate their differences.

On the Granular Representation of Fuzzy Quantifier-Based Fuzzy Rough Sets

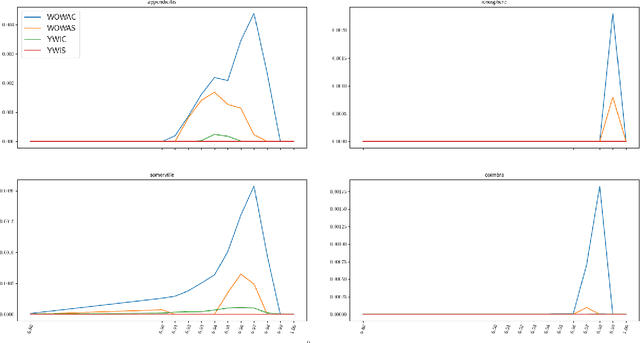
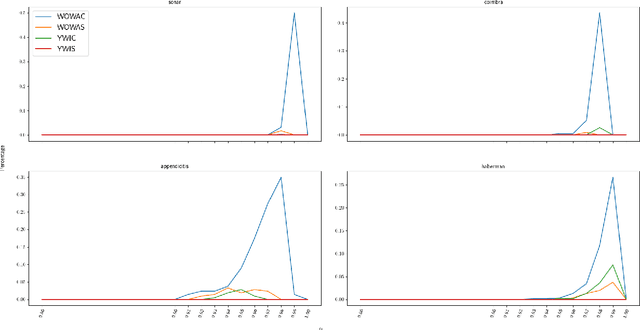
Rough set theory is a well-known mathematical framework that can deal with inconsistent data by providing lower and upper approximations of concepts. A prominent property of these approximations is their granular representation: that is, they can be written as unions of simple sets, called granules. The latter can be identified with "if. . . , then. . . " rules, which form the backbone of rough set rule induction. It has been shown previously that this property can be maintained for various fuzzy rough set models, including those based on ordered weighted average (OWA) operators. In this paper, we will focus on some instances of the general class of fuzzy quantifier-based fuzzy rough sets (FQFRS). In these models, the lower and upper approximations are evaluated using binary and unary fuzzy quantifiers, respectively. One of the main targets of this study is to examine the granular representation of different models of FQFRS. The main findings reveal that Choquet-based fuzzy rough sets can be represented granularly under the same conditions as OWA-based fuzzy rough sets, whereas Sugeno-based FRS can always be represented granularly. This observation highlights the potential of these models for resolving data inconsistencies and managing noise.

Fuzzy Rough Sets Based on Fuzzy Quantification

One of the weaknesses of classical (fuzzy) rough sets is their sensitivity to noise, which is particularly undesirable for machine learning applications. One approach to solve this issue is by making use of fuzzy quantifiers, as done by the vaguely quantified fuzzy rough set (VQFRS) model. While this idea is intuitive, the VQFRS model suffers from both theoretical flaws as well as from suboptimal performance in applications. In this paper, we improve on VQFRS by introducing fuzzy quantifier-based fuzzy rough sets (FQFRS), an intuitive generalization of fuzzy rough sets that makes use of general unary and binary quantification models. We show how several existing models fit in this generalization as well as how it inspires novel ones. Several binary quantification models are proposed to be used with FQFRS. We conduct a theoretical study of their properties, and investigate their potential by applying them to classification problems. In particular, we highlight Yager's Weighted Implication-based (YWI) binary quantification model, which induces a fuzzy rough set model that is both a significant improvement on VQFRS, as well as a worthy competitor to the popular ordered weighted averaging based fuzzy rough set (OWAFRS) model.

Choquet-Based Fuzzy Rough Sets

Fuzzy rough set theory can be used as a tool for dealing with inconsistent data when there is a gradual notion of indiscernibility between objects. It does this by providing lower and upper approximations of concepts. In classical fuzzy rough sets, the lower and upper approximations are determined using the minimum and maximum operators, respectively. This is undesirable for machine learning applications, since it makes these approximations sensitive to outlying samples. To mitigate this problem, ordered weighted average (OWA) based fuzzy rough sets were introduced. In this paper, we show how the OWA-based approach can be interpreted intuitively in terms of vague quantification, and then generalize it to Choquet-based fuzzy rough sets (CFRS). This generalization maintains desirable theoretical properties, such as duality and monotonicity. Furthermore, it provides more flexibility for machine learning applications. In particular, we show that it enables the seamless integration of outlier detection algorithms, to enhance the robustness of machine learning algorithms based on fuzzy rough sets.