FRRI: a novel algorithm for fuzzy-rough rule induction

Interpretability is the next frontier in machine learning research. In the search for white box models - as opposed to black box models, like random forests or neural networks - rule induction algorithms are a logical and promising option, since the rules can easily be understood by humans. Fuzzy and rough set theory have been successfully applied to this archetype, almost always separately. As both approaches to rule induction involve granular computing based on the concept of equivalence classes, it is natural to combine them. The QuickRules\cite{JensenCornelis2009} algorithm was a first attempt at using fuzzy rough set theory for rule induction. It is based on QuickReduct, a greedy algorithm for building decision reducts. QuickRules already showed an improvement over other rule induction methods. However, to evaluate the full potential of a fuzzy rough rule induction algorithm, one needs to start from the foundations. In this paper, we introduce a novel rule induction algorithm called Fuzzy Rough Rule Induction (FRRI). We provide background and explain the workings of our algorithm. Furthermore, we perform a computational experiment to evaluate the performance of our algorithm and compare it to other state-of-the-art rule induction approaches. We find that our algorithm is more accurate while creating small rulesets consisting of relatively short rules. We end the paper by outlining some directions for future work.

A unified weighting framework for evaluating nearest neighbour classification

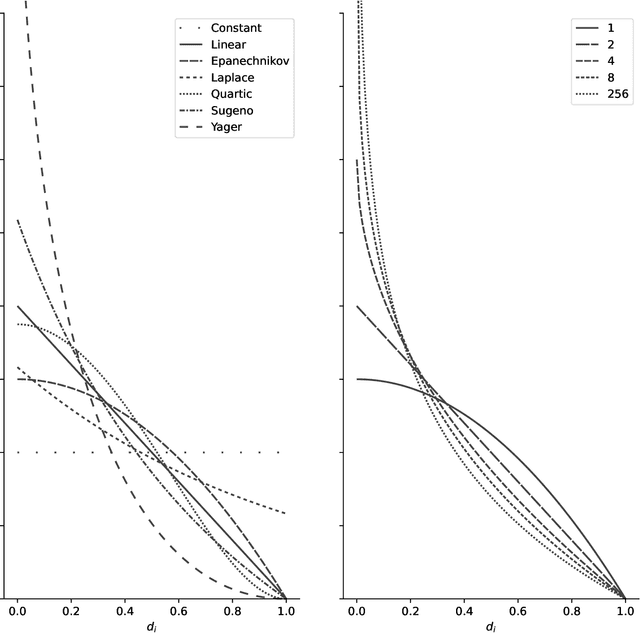
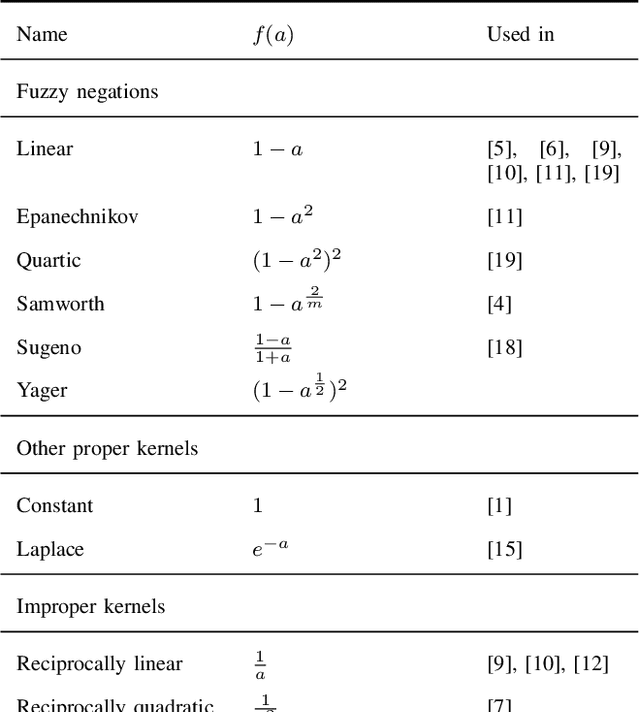
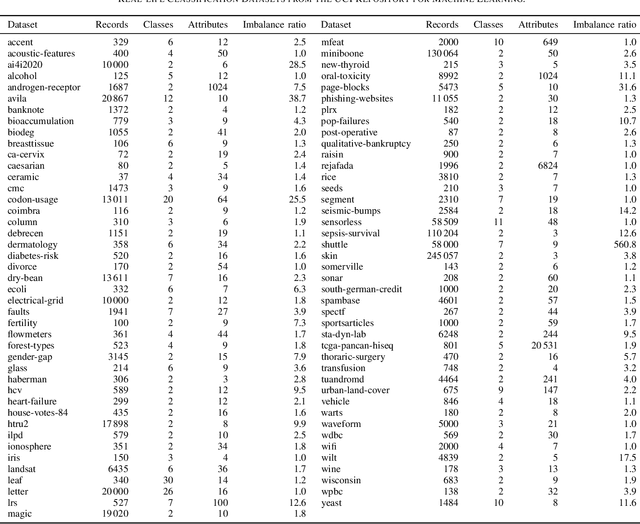
We present the first comprehensive and large-scale evaluation of classical (NN), fuzzy (FNN) and fuzzy rough (FRNN) nearest neighbour classification. We show that existing proposals for nearest neighbour weighting can be standardised in the form of kernel functions, applied to the distance values and/or ranks of the nearest neighbours of a test instance. Furthermore, we identify three commonly used distance functions and four scaling measures. We systematically evaluate these choices on a collection of 85 real-life classification datasets. We find that NN, FNN and FRNN all perform best with Boscovich distance. NN and FRNN perform best with a combination of Samworth rank- and distance weights and scaling by the mean absolute deviation around the median ($r_1$), the standard deviaton ($r_2$) or the interquartile range ($r_{\infty}^*$), while FNN performs best with only Samworth distance-weights and $r_1$- or $r_2$-scaling. We also introduce a new kernel based on fuzzy Yager negation, and show that NN achieves comparable performance with Yager distance-weights, which are simpler to implement than a combination of Samworth distance- and rank-weights. Finally, we demonstrate that FRNN generally outperforms NN, which in turns performs systematically better than FNN.

Evaluation of the impact of the indiscernibility relation on the fuzzy-rough nearest neighbours algorithm

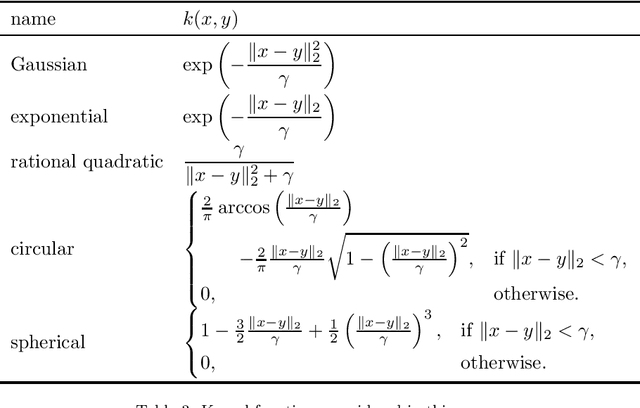
Fuzzy rough sets are well-suited for working with vague, imprecise or uncertain information and have been succesfully applied in real-world classification problems. One of the prominent representatives of this theory is fuzzy-rough nearest neighbours (FRNN), a classification algorithm based on the classical k-nearest neighbours algorithm. The crux of FRNN is the indiscernibility relation, which measures how similar two elements in the data set of interest are. In this paper, we investigate the impact of this indiscernibility relation on the performance of FRNN classification. In addition to relations based on distance functions and kernels, we also explore the effect of distance metric learning on FRNN for the first time. Furthermore, we also introduce an asymmetric, class-specific relation based on the Mahalanobis distance which uses the correlation within each class, and which shows a significant improvement over the regular Mahalanobis distance, but is still beaten by the Manhattan distance. Overall, the Neighbourhood Components Analysis algorithm is found to be the best performer, trading speed for accuracy.