FRRI: a novel algorithm for fuzzy-rough rule induction

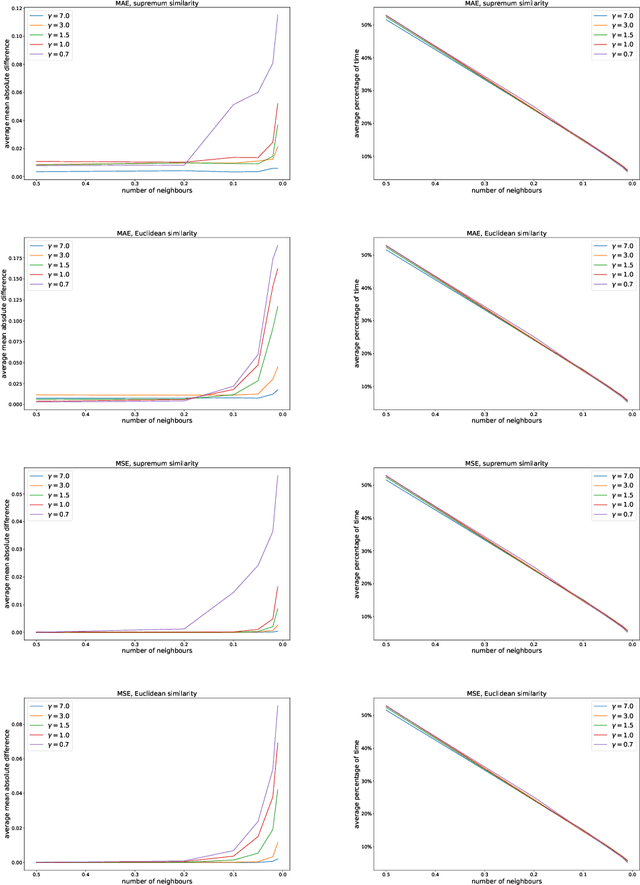
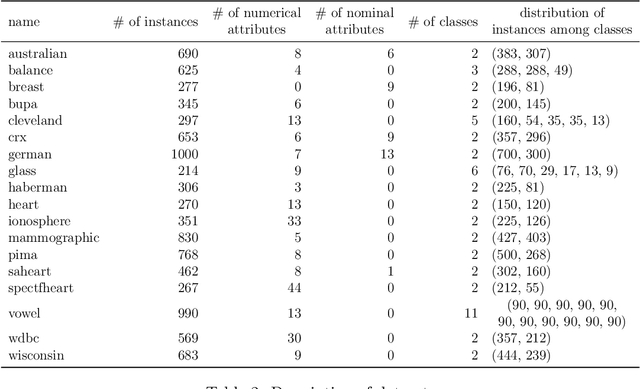
Interpretability is the next frontier in machine learning research. In the search for white box models - as opposed to black box models, like random forests or neural networks - rule induction algorithms are a logical and promising option, since the rules can easily be understood by humans. Fuzzy and rough set theory have been successfully applied to this archetype, almost always separately. As both approaches to rule induction involve granular computing based on the concept of equivalence classes, it is natural to combine them. The QuickRules\cite{JensenCornelis2009} algorithm was a first attempt at using fuzzy rough set theory for rule induction. It is based on QuickReduct, a greedy algorithm for building decision reducts. QuickRules already showed an improvement over other rule induction methods. However, to evaluate the full potential of a fuzzy rough rule induction algorithm, one needs to start from the foundations. In this paper, we introduce a novel rule induction algorithm called Fuzzy Rough Rule Induction (FRRI). We provide background and explain the workings of our algorithm. Furthermore, we perform a computational experiment to evaluate the performance of our algorithm and compare it to other state-of-the-art rule induction approaches. We find that our algorithm is more accurate while creating small rulesets consisting of relatively short rules. We end the paper by outlining some directions for future work.

Fuzzy granular approximation classifier

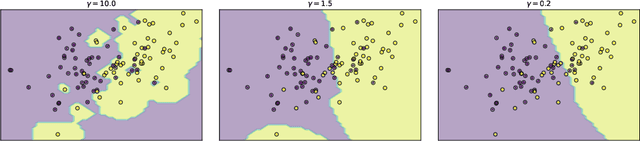
In this article, a new Fuzzy Granular Approximation Classifier (FGAC) is introduced. The classifier is based on the previously introduced concept of the granular approximation and its multi-class classification case. The classifier is instance-based and its biggest advantage is its local transparency i.e., the ability to explain every individual prediction it makes. We first develop the FGAC for the binary classification case and the multi-class classification case and we discuss its variation that includes the Ordered Weighted Average (OWA) operators. Those variations of the FGAC are then empirically compared with other locally transparent ML methods. At the end, we discuss the transparency of the FGAC and its advantage over other locally transparent methods. We conclude that while the FGAC has similar predictive performance to other locally transparent ML models, its transparency can be superior in certain cases.

Multi-class granular approximation by means of disjoint and adjacent fuzzy granules

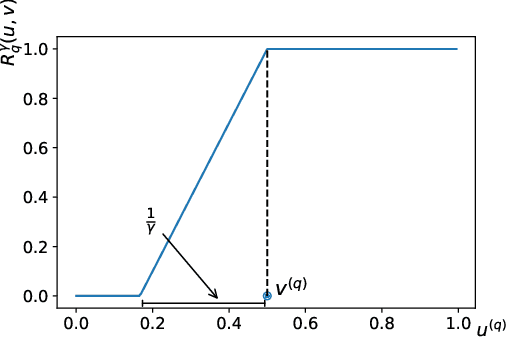
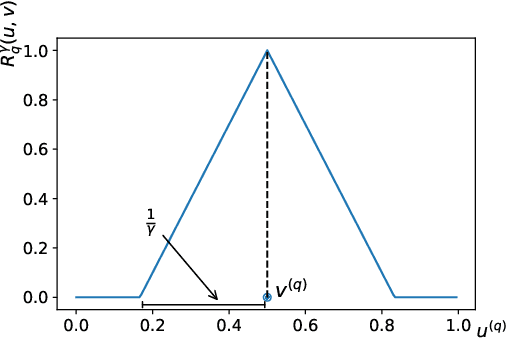
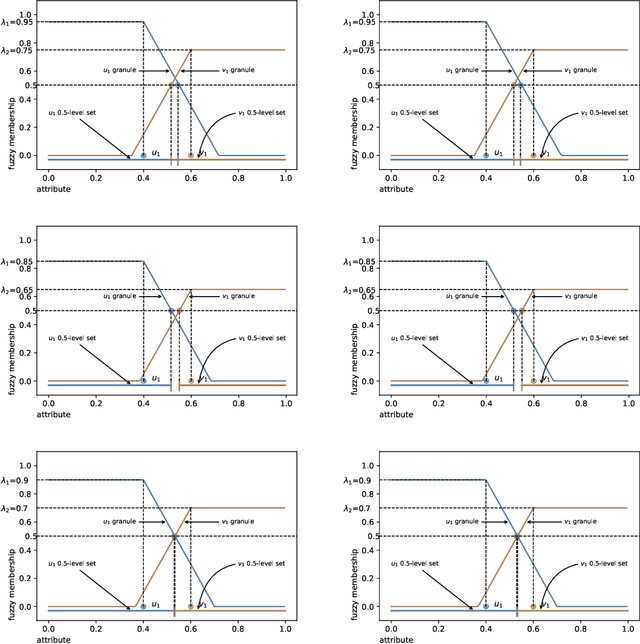
In granular computing, fuzzy sets can be approximated by granularly representable sets that are as close as possible to the original fuzzy set w.r.t. a given closeness measure. Such sets are called granular approximations. In this article, we introduce the concepts of disjoint and adjacent granules and we examine how the new definitions affect the granular approximations. First, we show that the new concepts are important for binary classification problems since they help to keep decision regions separated (disjoint granules) and at the same time to cover as much as possible of the attribute space (adjacent granules). Later, we consider granular approximations for multi-class classification problems leading to the definition of a multi-class granular approximation. Finally, we show how to efficiently calculate multi-class granular approximations for {\L}ukasiewicz fuzzy connectives. We also provide graphical illustrations for a better understanding of the introduced concepts.

A Novel Machine Learning Approach to Data Inconsistency with respect to a Fuzzy Relation

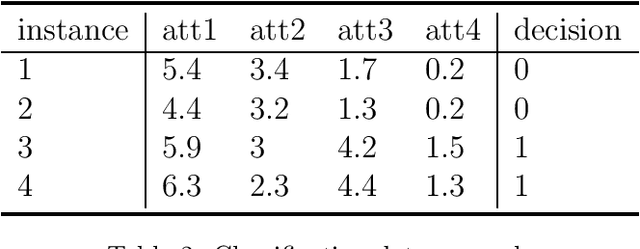
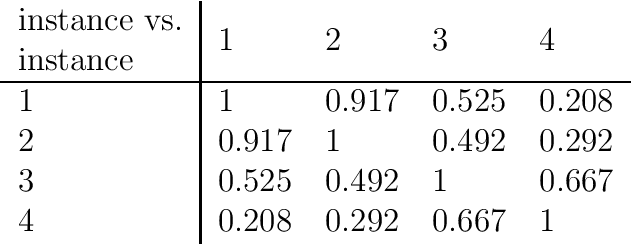
Inconsistency in prediction problems occurs when instances that relate in a certain way on condition attributes, do not follow the same relation on the decision attribute. For example, in ordinal classification with monotonicity constraints, it occurs when an instance dominating another instance on condition attributes has been assigned to a worse decision class. It typically appears as a result of perturbation in data caused by incomplete knowledge (missing attributes) or by random effects that occur during data generation (instability in the assessment of decision attribute values). Inconsistencies with respect to a crisp preorder relation (expressing either dominance or indiscernibility between instances) can be handled using symbolic approaches like rough set theory and by using statistical/machine learning approaches that involve optimization methods. Fuzzy rough sets can also be seen as a symbolic approach to inconsistency handling with respect to a fuzzy relation. In this article, we introduce a new machine learning method for inconsistency handling with respect to a fuzzy preorder relation. The novel approach is motivated by the existing machine learning approach used for crisp relations. We provide statistical foundations for it and develop optimization procedures that can be used to eliminate inconsistencies. The article also proves important properties and contains didactic examples of those procedures.