A Novel Machine Learning Approach to Data Inconsistency with respect to a Fuzzy Relation
Paper and Code
Nov 26, 2021
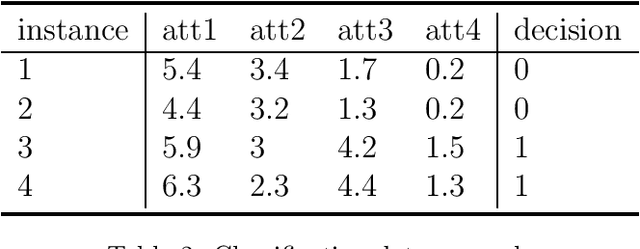
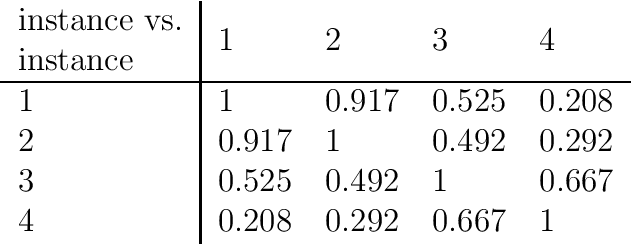

Inconsistency in prediction problems occurs when instances that relate in a certain way on condition attributes, do not follow the same relation on the decision attribute. For example, in ordinal classification with monotonicity constraints, it occurs when an instance dominating another instance on condition attributes has been assigned to a worse decision class. It typically appears as a result of perturbation in data caused by incomplete knowledge (missing attributes) or by random effects that occur during data generation (instability in the assessment of decision attribute values). Inconsistencies with respect to a crisp preorder relation (expressing either dominance or indiscernibility between instances) can be handled using symbolic approaches like rough set theory and by using statistical/machine learning approaches that involve optimization methods. Fuzzy rough sets can also be seen as a symbolic approach to inconsistency handling with respect to a fuzzy relation. In this article, we introduce a new machine learning method for inconsistency handling with respect to a fuzzy preorder relation. The novel approach is motivated by the existing machine learning approach used for crisp relations. We provide statistical foundations for it and develop optimization procedures that can be used to eliminate inconsistencies. The article also proves important properties and contains didactic examples of those procedures.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge