Multi-class granular approximation by means of disjoint and adjacent fuzzy granules
Paper and Code
Feb 15, 2022
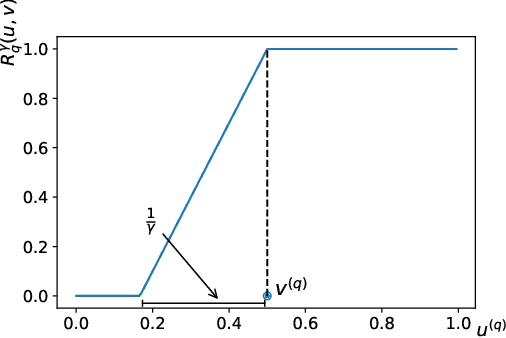
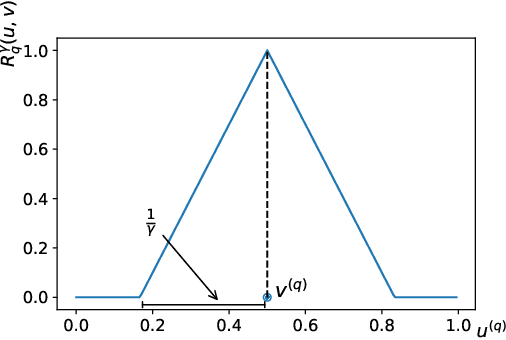
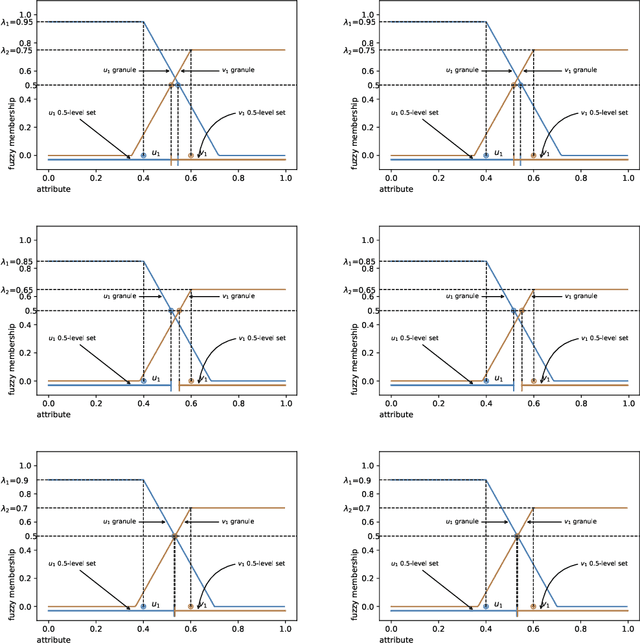
In granular computing, fuzzy sets can be approximated by granularly representable sets that are as close as possible to the original fuzzy set w.r.t. a given closeness measure. Such sets are called granular approximations. In this article, we introduce the concepts of disjoint and adjacent granules and we examine how the new definitions affect the granular approximations. First, we show that the new concepts are important for binary classification problems since they help to keep decision regions separated (disjoint granules) and at the same time to cover as much as possible of the attribute space (adjacent granules). Later, we consider granular approximations for multi-class classification problems leading to the definition of a multi-class granular approximation. Finally, we show how to efficiently calculate multi-class granular approximations for {\L}ukasiewicz fuzzy connectives. We also provide graphical illustrations for a better understanding of the introduced concepts.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge