A unified weighting framework for evaluating nearest neighbour classification
Paper and Code
Nov 28, 2023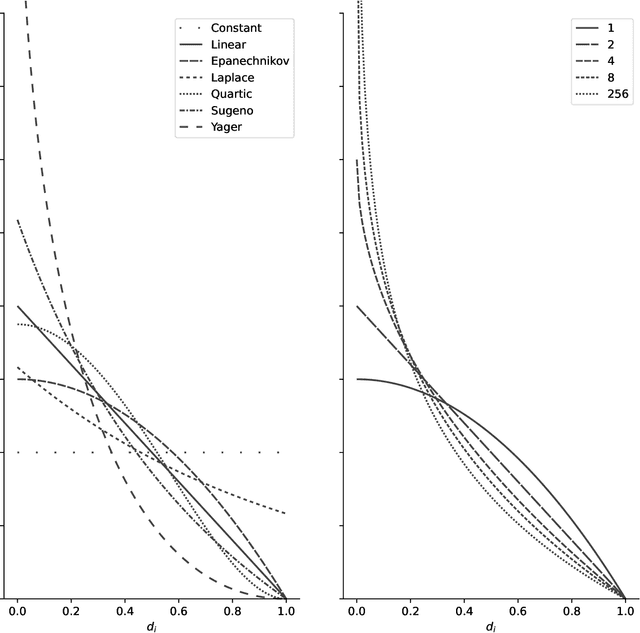
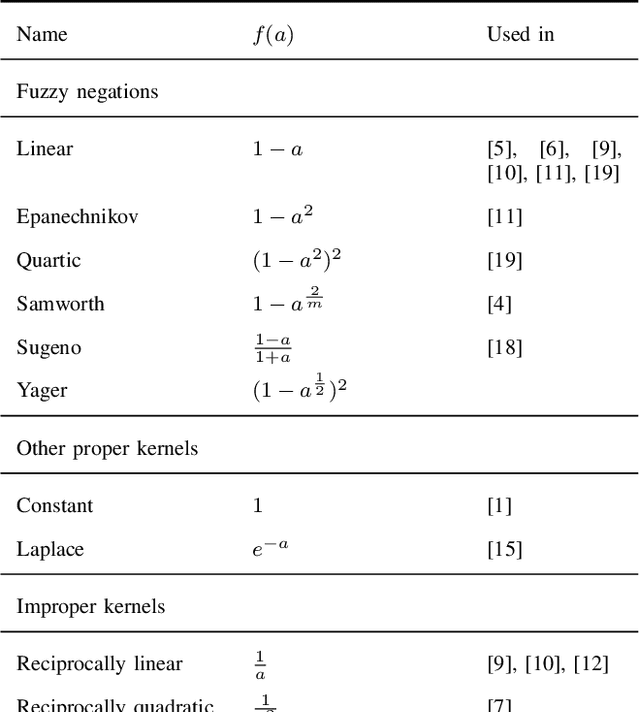
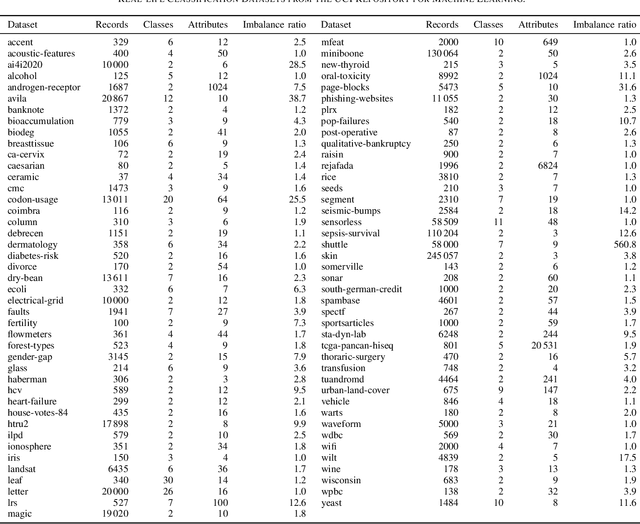

We present the first comprehensive and large-scale evaluation of classical (NN), fuzzy (FNN) and fuzzy rough (FRNN) nearest neighbour classification. We show that existing proposals for nearest neighbour weighting can be standardised in the form of kernel functions, applied to the distance values and/or ranks of the nearest neighbours of a test instance. Furthermore, we identify three commonly used distance functions and four scaling measures. We systematically evaluate these choices on a collection of 85 real-life classification datasets. We find that NN, FNN and FRNN all perform best with Boscovich distance. NN and FRNN perform best with a combination of Samworth rank- and distance weights and scaling by the mean absolute deviation around the median ($r_1$), the standard deviaton ($r_2$) or the interquartile range ($r_{\infty}^*$), while FNN performs best with only Samworth distance-weights and $r_1$- or $r_2$-scaling. We also introduce a new kernel based on fuzzy Yager negation, and show that NN achieves comparable performance with Yager distance-weights, which are simpler to implement than a combination of Samworth distance- and rank-weights. Finally, we demonstrate that FRNN generally outperforms NN, which in turns performs systematically better than FNN.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge