Topologically Regularized Data Embeddings

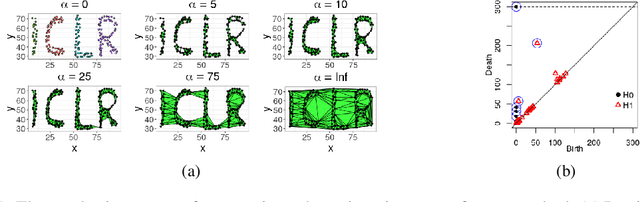
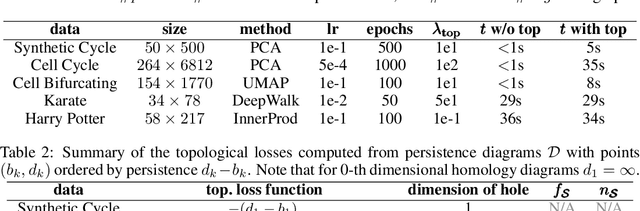
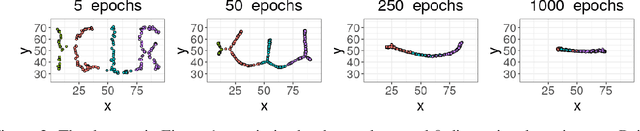
Unsupervised representation learning methods are widely used for gaining insight into high-dimensional, unstructured, or structured data. In some cases, users may have prior topological knowledge about the data, such as a known cluster structure or the fact that the data is known to lie along a tree- or graph-structured topology. However, generic methods to ensure such structure is salient in the low-dimensional representations are lacking. This negatively impacts the interpretability of low-dimensional embeddings, and plausibly downstream learning tasks. To address this issue, we introduce topological regularization: a generic approach based on algebraic topology to incorporate topological prior knowledge into low-dimensional embeddings. We introduce a class of topological loss functions, and show that jointly optimizing an embedding loss with such a topological loss function as a regularizer yields embeddings that reflect not only local proximities but also the desired topological structure. We include a self-contained overview of the required foundational concepts in algebraic topology, and provide intuitive guidance on how to design topological loss functions for a variety of shapes, such as clusters, cycles, and bifurcations. We empirically evaluate the proposed approach on computational efficiency, robustness, and versatility in combination with linear and non-linear dimensionality reduction and graph embedding methods.

The Curse Revisited: a Newly Quantified Concept of Meaningful Distances for Learning from High-Dimensional Noisy Data

Distances between data points are widely used in point cloud representation learning. Yet, it is no secret that under the effect of noise, these distances-and thus the models based upon them-may lose their usefulness in high dimensions. Indeed, the small marginal effects of the noise may then accumulate quickly, shifting empirical closest and furthest neighbors away from the ground truth. In this paper, we characterize such effects in high-dimensional data using an asymptotic probabilistic expression. Furthermore, while it has been previously argued that neighborhood queries become meaningless and unstable when there is a poor relative discrimination between the furthest and closest point, we conclude that this is not necessarily the case when explicitly separating the ground truth data from the noise. More specifically, we derive that under particular conditions, empirical neighborhood relations affected by noise are still likely to be true even when we observe this discrimination to be poor. We include thorough empirical verification of our results, as well as experiments that interestingly show our derived phase shift where neighbors become random or not is identical to the phase shift where common dimensionality reduction methods perform poorly or well for finding low-dimensional representations of high-dimensional data with dense noise.