InfoClus: Informative Clustering of High-dimensional Data Embeddings

Developing an understanding of high-dimensional data can be facilitated by visualizing that data using dimensionality reduction. However, the low-dimensional embeddings are often difficult to interpret. To facilitate the exploration and interpretation of low-dimensional embeddings, we introduce a new concept named partitioning with explanations. The idea is to partition the data shown through the embedding into groups, each of which is given a sparse explanation using the original high-dimensional attributes. We introduce an objective function that quantifies how much we can learn through observing the explanations of the data partitioning, using information theory, and also how complex the explanations are. Through parameterization of the complexity, we can tune the solutions towards the desired granularity. We propose InfoClus, which optimizes the partitioning and explanations jointly, through greedy search constrained over a hierarchical clustering. We conduct a qualitative and quantitative analysis of InfoClus on three data sets. We contrast the results on the Cytometry data with published manual analysis results, and compare with two other recent methods for explaining embeddings (RVX and VERA). These comparisons highlight that InfoClus has distinct advantages over existing procedures and methods. We find that InfoClus can automatically create good starting points for the analysis of dimensionality-reduction-based scatter plots.

Large Language Models Reflect the Ideology of their Creators

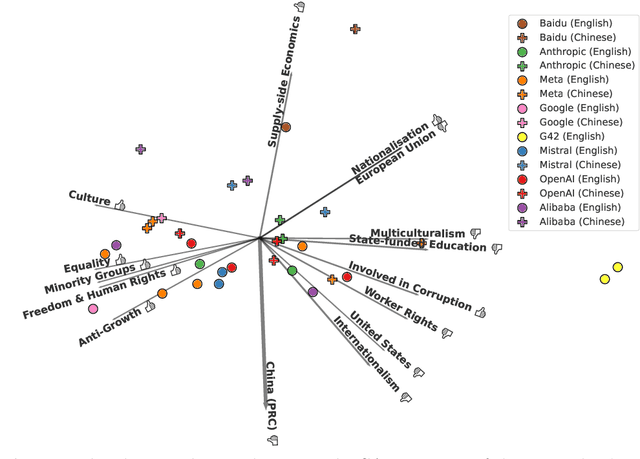
Large language models (LLMs) are trained on vast amounts of data to generate natural language, enabling them to perform tasks like text summarization and question answering. These models have become popular in artificial intelligence (AI) assistants like ChatGPT and already play an influential role in how humans access information. However, the behavior of LLMs varies depending on their design, training, and use. In this paper, we uncover notable diversity in the ideological stance exhibited across different LLMs and languages in which they are accessed. We do this by prompting a diverse panel of popular LLMs to describe a large number of prominent and controversial personalities from recent world history, both in English and in Chinese. By identifying and analyzing moral assessments reflected in the generated descriptions, we find consistent normative differences between how the same LLM responds in Chinese compared to English. Similarly, we identify normative disagreements between Western and non-Western LLMs about prominent actors in geopolitical conflicts. Furthermore, popularly hypothesized disparities in political goals among Western models are reflected in significant normative differences related to inclusion, social inequality, and political scandals. Our results show that the ideological stance of an LLM often reflects the worldview of its creators. This raises important concerns around technological and regulatory efforts with the stated aim of making LLMs ideologically `unbiased', and it poses risks for political instrumentalization.

Pattern or Artifact? Interactively Exploring Embedding Quality with TRACE

This paper presents TRACE, a tool to analyze the quality of 2D embeddings generated through dimensionality reduction techniques. Dimensionality reduction methods often prioritize preserving either local neighborhoods or global distances, but insights from visual structures can be misleading if the objective has not been achieved uniformly. TRACE addresses this challenge by providing a scalable and extensible pipeline for computing both local and global quality measures. The interactive browser-based interface allows users to explore various embeddings while visually assessing the pointwise embedding quality. The interface also facilitates in-depth analysis by highlighting high-dimensional nearest neighbors for any group of points and displaying high-dimensional distances between points. TRACE enables analysts to make informed decisions regarding the most suitable dimensionality reduction method for their specific use case, by showing the degree and location where structure is preserved in the reduced space.

Revised Conditional t-SNE: Looking Beyond the Nearest Neighbors

Conditional t-SNE (ct-SNE) is a recent extension to t-SNE that allows removal of known cluster information from the embedding, to obtain a visualization revealing structure beyond label information. This is useful, for example, when one wants to factor out unwanted differences between a set of classes. We show that ct-SNE fails in many realistic settings, namely if the data is well clustered over the labels in the original high-dimensional space. We introduce a revised method by conditioning the high-dimensional similarities instead of the low-dimensional similarities and storing within- and across-label nearest neighbors separately. This also enables the use of recently proposed speedups for t-SNE, improving the scalability. From experiments on synthetic data, we find that our proposed method resolves the considered problems and improves the embedding quality. On real data containing batch effects, the expected improvement is not always there. We argue revised ct-SNE is preferable overall, given its improved scalability. The results also highlight new open questions, such as how to handle distance variations between clusters.

Topologically Regularized Data Embeddings

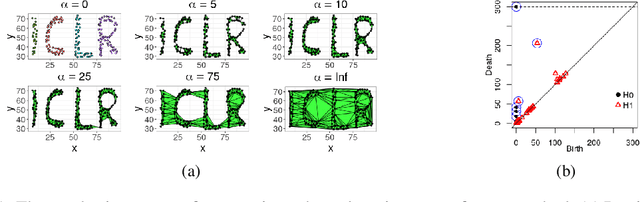
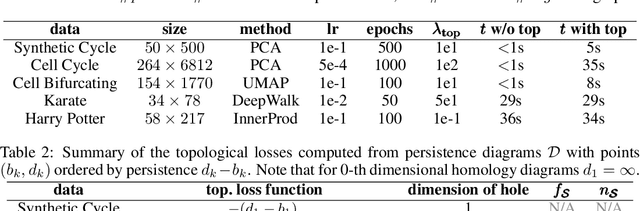
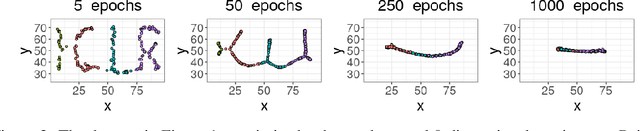
Unsupervised representation learning methods are widely used for gaining insight into high-dimensional, unstructured, or structured data. In some cases, users may have prior topological knowledge about the data, such as a known cluster structure or the fact that the data is known to lie along a tree- or graph-structured topology. However, generic methods to ensure such structure is salient in the low-dimensional representations are lacking. This negatively impacts the interpretability of low-dimensional embeddings, and plausibly downstream learning tasks. To address this issue, we introduce topological regularization: a generic approach based on algebraic topology to incorporate topological prior knowledge into low-dimensional embeddings. We introduce a class of topological loss functions, and show that jointly optimizing an embedding loss with such a topological loss function as a regularizer yields embeddings that reflect not only local proximities but also the desired topological structure. We include a self-contained overview of the required foundational concepts in algebraic topology, and provide intuitive guidance on how to design topological loss functions for a variety of shapes, such as clusters, cycles, and bifurcations. We empirically evaluate the proposed approach on computational efficiency, robustness, and versatility in combination with linear and non-linear dimensionality reduction and graph embedding methods.

ExClus: Explainable Clustering on Low-dimensional Data Representations

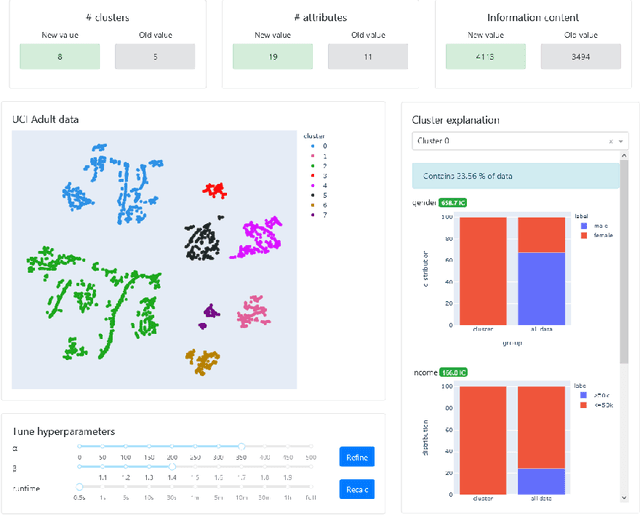
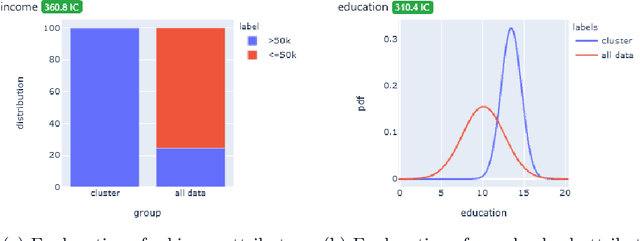
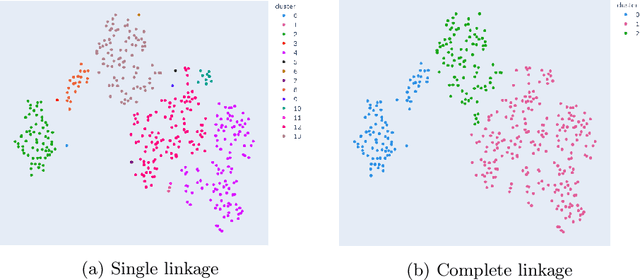
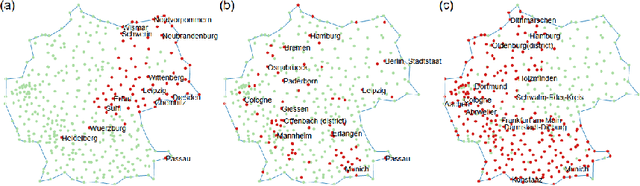
Dimensionality reduction and clustering techniques are frequently used to analyze complex data sets, but their results are often not easy to interpret. We consider how to support users in interpreting apparent cluster structure on scatter plots where the axes are not directly interpretable, such as when the data is projected onto a two-dimensional space using a dimensionality-reduction method. Specifically, we propose a new method to compute an interpretable clustering automatically, where the explanation is in the original high-dimensional space and the clustering is coherent in the low-dimensional projection. It provides a tunable balance between the complexity and the amount of information provided, through the use of information theory. We study the computational complexity of this problem and introduce restrictions on the search space of solutions to arrive at an efficient, tunable, greedy optimization algorithm. This algorithm is furthermore implemented in an interactive tool called ExClus. Experiments on several data sets highlight that ExClus can provide informative and easy-to-understand patterns, and they expose where the algorithm is efficient and where there is room for improvement considering tunability and scalability.

Factoring out prior knowledge from low-dimensional embeddings

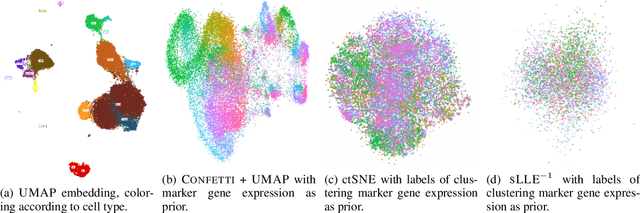
Low-dimensional embedding techniques such as tSNE and UMAP allow visualizing high-dimensional data and therewith facilitate the discovery of interesting structure. Although they are widely used, they visualize data as is, rather than in light of the background knowledge we have about the data. What we already know, however, strongly determines what is novel and hence interesting. In this paper we propose two methods for factoring out prior knowledge in the form of distance matrices from low-dimensional embeddings. To factor out prior knowledge from tSNE embeddings, we propose JEDI that adapts the tSNE objective in a principled way using Jensen-Shannon divergence. To factor out prior knowledge from any downstream embedding approach, we propose CONFETTI, in which we directly operate on the input distance matrices. Extensive experiments on both synthetic and real world data show that both methods work well, providing embeddings that exhibit meaningful structure that would otherwise remain hidden.