Factoring out prior knowledge from low-dimensional embeddings
Paper and Code
Mar 02, 2021

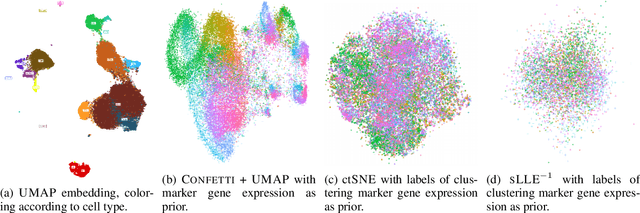

Low-dimensional embedding techniques such as tSNE and UMAP allow visualizing high-dimensional data and therewith facilitate the discovery of interesting structure. Although they are widely used, they visualize data as is, rather than in light of the background knowledge we have about the data. What we already know, however, strongly determines what is novel and hence interesting. In this paper we propose two methods for factoring out prior knowledge in the form of distance matrices from low-dimensional embeddings. To factor out prior knowledge from tSNE embeddings, we propose JEDI that adapts the tSNE objective in a principled way using Jensen-Shannon divergence. To factor out prior knowledge from any downstream embedding approach, we propose CONFETTI, in which we directly operate on the input distance matrices. Extensive experiments on both synthetic and real world data show that both methods work well, providing embeddings that exhibit meaningful structure that would otherwise remain hidden.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge