Medical-Knowledge Driven Multiple Instance Learning for Classifying Severe Abdominal Anomalies on Prenatal Ultrasound

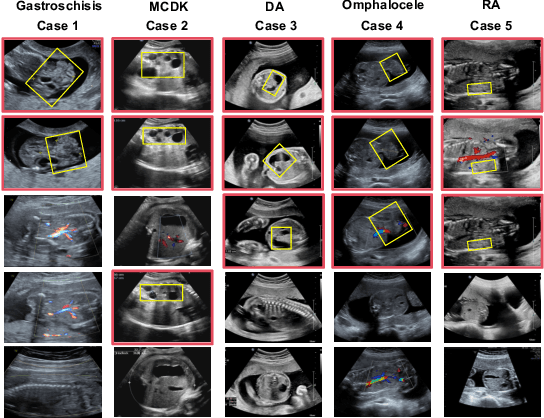
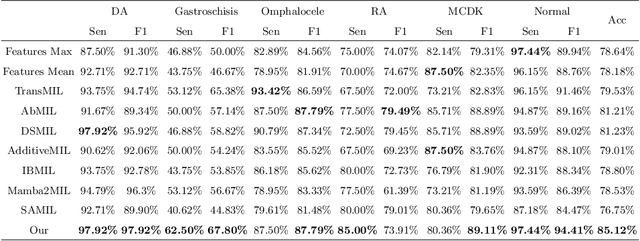
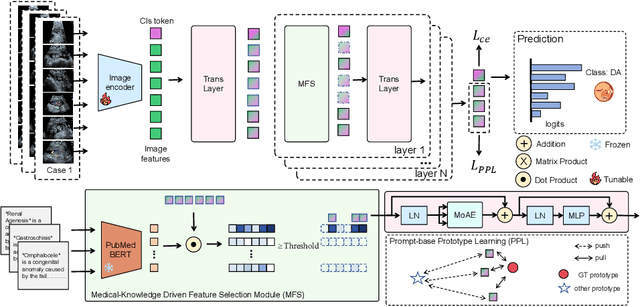
Fetal abdominal malformations are serious congenital anomalies that require accurate diagnosis to guide pregnancy management and reduce mortality. Although AI has demonstrated significant potential in medical diagnosis, its application to prenatal abdominal anomalies remains limited. Most existing studies focus on image-level classification and rely on standard plane localization, placing less emphasis on case-level diagnosis. In this paper, we develop a case-level multiple instance learning (MIL)-based method, free of standard plane localization, for classifying fetal abdominal anomalies in prenatal ultrasound. Our contribution is three-fold. First, we adopt a mixture-of-attention-experts module (MoAE) to weight different attention heads for various planes. Secondly, we propose a medical-knowledge-driven feature selection module (MFS) to align image features with medical knowledge, performing self-supervised image token selection at the case-level. Finally, we propose a prompt-based prototype learning (PPL) to enhance the MFS. Extensively validated on a large prenatal abdominal ultrasound dataset containing 2,419 cases, with a total of 24,748 images and 6 categories, our proposed method outperforms the state-of-the-art competitors. Codes are available at:https://github.com/LL-AC/AAcls.

Remote Rowhammer Attack using Adversarial Observations on Federated Learning Clients

Federated Learning (FL) has the potential for simultaneous global learning amongst a large number of parallel agents, enabling emerging AI such as LLMs to be trained across demographically diverse data. Central to this being efficient is the ability for FL to perform sparse gradient updates and remote direct memory access at the central server. Most of the research in FL security focuses on protecting data privacy at the edge client or in the communication channels between the client and server. Client-facing attacks on the server are less well investigated as the assumption is that a large collective of clients offer resilience. Here, we show that by attacking certain clients that lead to a high frequency repetitive memory update in the server, we can remote initiate a rowhammer attack on the server memory. For the first time, we do not need backdoor access to the server, and a reinforcement learning (RL) attacker can learn how to maximize server repetitive memory updates by manipulating the client's sensor observation. The consequence of the remote rowhammer attack is that we are able to achieve bit flips, which can corrupt the server memory. We demonstrate the feasibility of our attack using a large-scale FL automatic speech recognition (ASR) systems with sparse updates, our adversarial attacking agent can achieve around 70\% repeated update rate (RUR) in the targeted server model, effectively inducing bit flips on server DRAM. The security implications are that can cause disruptions to learning or may inadvertently cause elevated privilege. This paves the way for further research on practical mitigation strategies in FL and hardware design.

A Plug-and-Play Untrained Neural Network for Full Waveform Inversion in Reconstructing Sound Speed Images of Ultrasound Computed Tomography

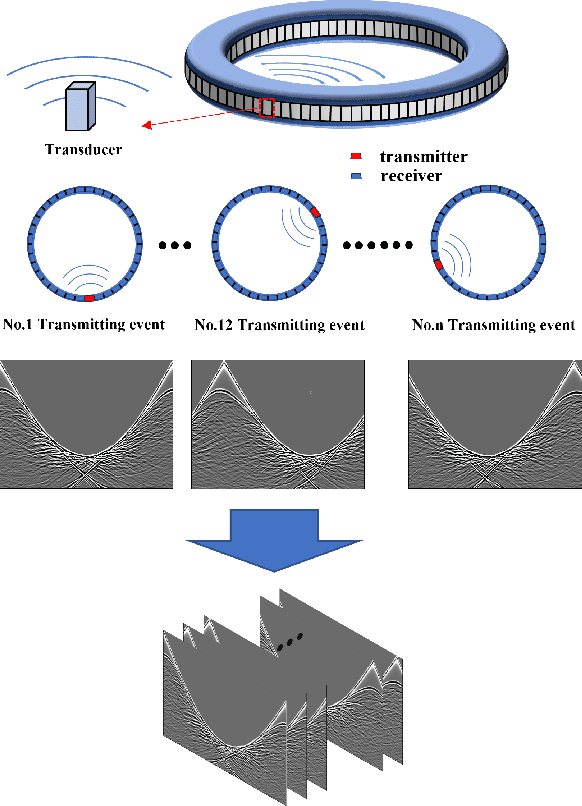
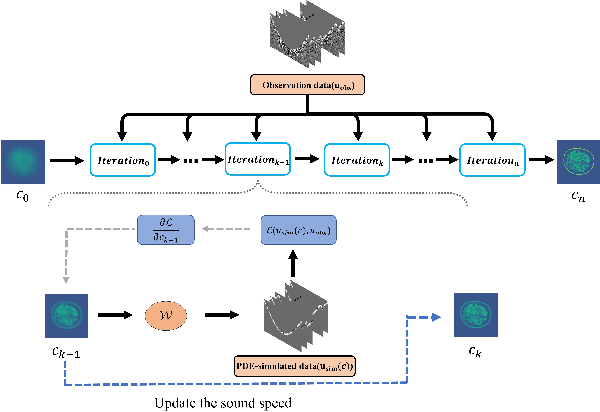
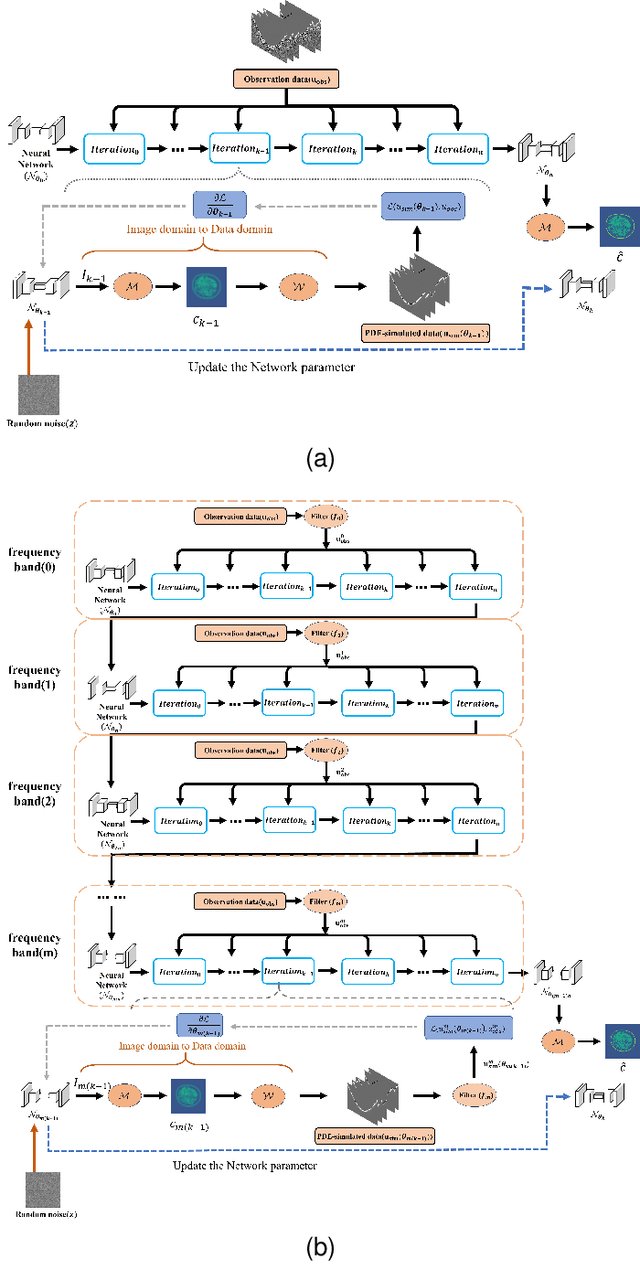
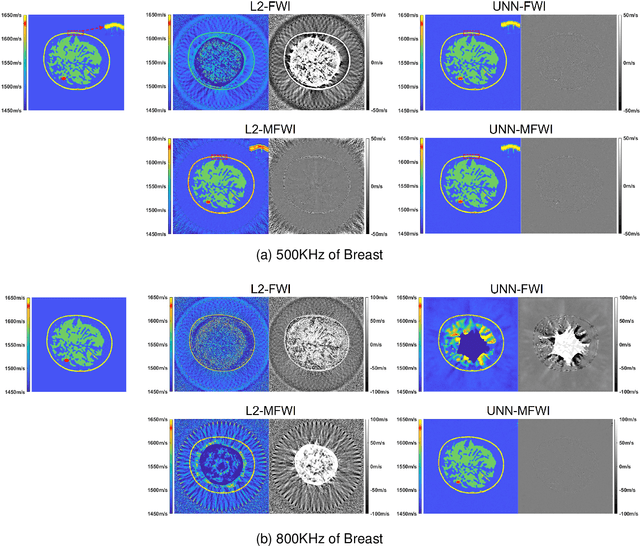
Ultrasound computed tomography (USCT), as an emerging technology, can provide multiple quantitative parametric images of human tissue, such as sound speed and attenuation images, distinguishing it from conventional B-mode (reflection) ultrasound imaging. Full waveform inversion (FWI) is acknowledged as a technique with the greatest potential for reconstructing high-resolution sound speed images in USCT. However, traditional FWI for sound speed image reconstruction suffers from high sensitivity to the initial model caused by its strong non-convex nonlinearity, resulting in poor performance when ultrasound signals are at high frequencies. This limitation significantly restricts the application of FWI in the USCT imaging field. In this paper, we propose an untrained neural network (UNN) that can be integrated into the traditional iteration-based FWI framework as an implicit regularization prior. This integration allows for seamless deployment as a plug-and-play module within existing FWI algorithms or their variants. Notably, the proposed UNN method can be trained in an unsupervised fashion, a vital aspect in medical imaging where ground truth data is often unavailable. Evaluations of the numerical simulation and phantom experiment of the breast demonstrate that the proposed UNN improves the robustness of image reconstruction, reduces image artifacts, and achieves great image contrast. To the best of our knowledge, this study represents the first attempt to propose an implicit UNN for FWI in reconstructing sound speed images for USCT.

Reconfigurable FPGA-Based Solvers For Sparse Satellite Control

This paper introduces a novel reconfigurable and power-efficient FPGA (Field-Programmable Gate Array) implementation of an operator splitting algorithm for Non-Terrestial Network's (NTN) relay satellites model predictive orientation control (MPC). Our approach ensures system stability and introduces an innovative reconfigurable bit-width FPGA-based optimization solver. To demonstrate its efficacy, we employ a real FPGA-In-the-Loop hardware setup to control simulated satellite dynamics. Furthermore, we conduct an in-depth comparative analysis, examining various fixed-point configurations to evaluate the combined system's closed-loop performance and power efficiency, providing a holistic understanding of the proposed implementation's advantages.

Masked Latent Transformer with the Random Masking Ratio to Advance the Diagnosis of Dental Fluorosis

Dental fluorosis is a chronic disease caused by long-term overconsumption of fluoride, which leads to changes in the appearance of tooth enamel. It is an important basis for early non-invasive diagnosis of endemic fluorosis. However, even dental professionals may not be able to accurately distinguish dental fluorosis and its severity based on tooth images. Currently, there is still a gap in research on applying deep learning to diagnosing dental fluorosis. Therefore, we construct the first open-source dental fluorosis image dataset (DFID), laying the foundation for deep learning research in this field. To advance the diagnosis of dental fluorosis, we propose a pioneering deep learning model called masked latent transformer with the random masking ratio (MLTrMR). MLTrMR introduces a mask latent modeling scheme based on Vision Transformer to enhance contextual learning of dental fluorosis lesion characteristics. Consisting of a latent embedder, encoder, and decoder, MLTrMR employs the latent embedder to extract latent tokens from the original image, whereas the encoder and decoder comprising the latent transformer (LT) block are used to process unmasked tokens and predict masked tokens, respectively. To mitigate the lack of inductive bias in Vision Transformer, which may result in performance degradation, the LT block introduces latent tokens to enhance the learning capacity of latent lesion features. Furthermore, we design an auxiliary loss function to constrain the parameter update direction of the model. MLTrMR achieves 80.19% accuracy, 75.79% F1, and 81.28% quadratic weighted kappa on DFID, making it state-of-the-art (SOTA).

A Low-Power Hardware-Friendly Optimisation Algorithm With Absolute Numerical Stability and Convergence Guarantees

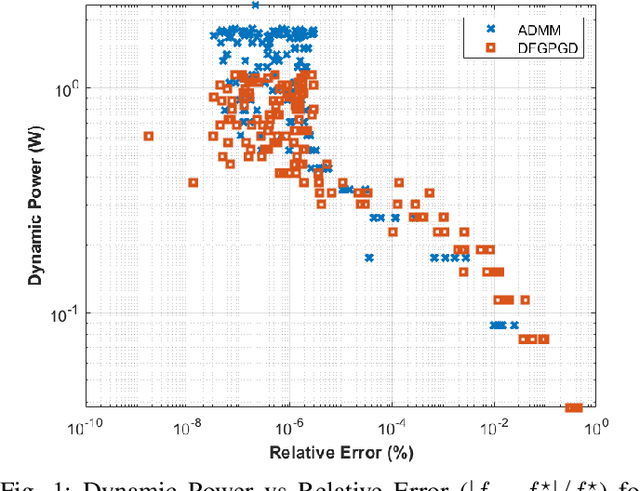
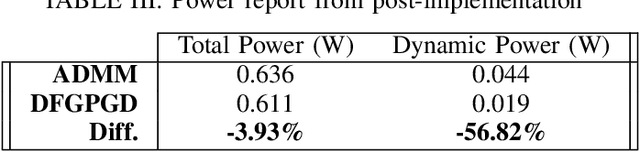
We propose Dual-Feedback Generalized Proximal Gradient Descent (DFGPGD) as a new, hardware-friendly, operator splitting algorithm. We then establish convergence guarantees under approximate computational errors and we derive theoretical criteria for the numerical stability of DFGPGD based on absolute stability of dynamical systems. We also propose a new generalized proximal ADMM that can be used to instantiate most of existing proximal-based composite optimization solvers. We implement DFGPGD and ADMM on FPGA ZCU106 board and compare them in light of FPGA's timing as well as resource utilization and power efficiency. We also perform a full-stack, application-to-hardware, comparison between approximate versions of DFGPGD and ADMM based on dynamic power/error rate trade-off, which is a new hardware-application combined metric.

Probabilistic Verification of Approximate Algorithms with Unstructured Errors: Application to Fully Inexact Generalized ADMM

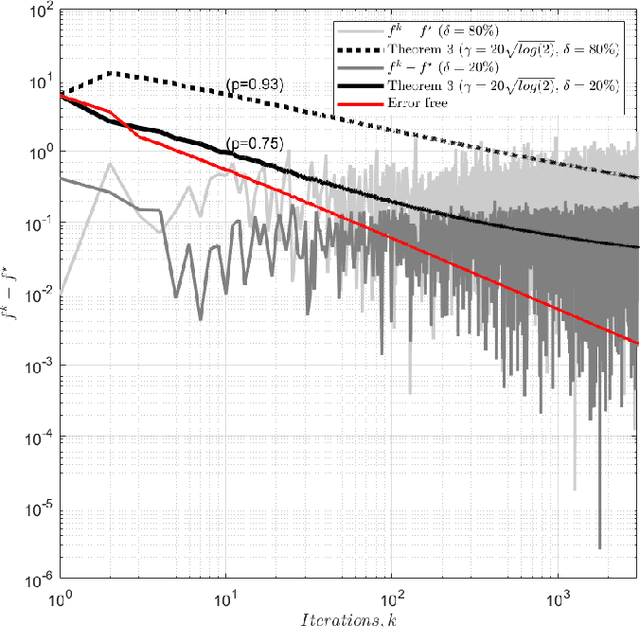
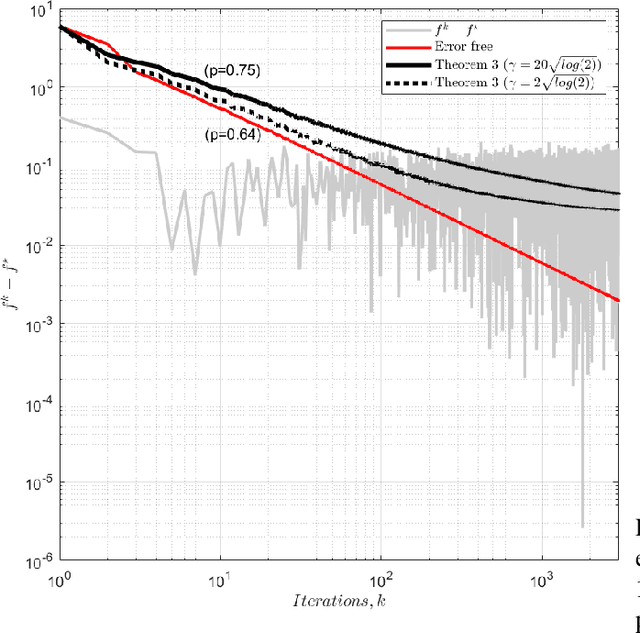
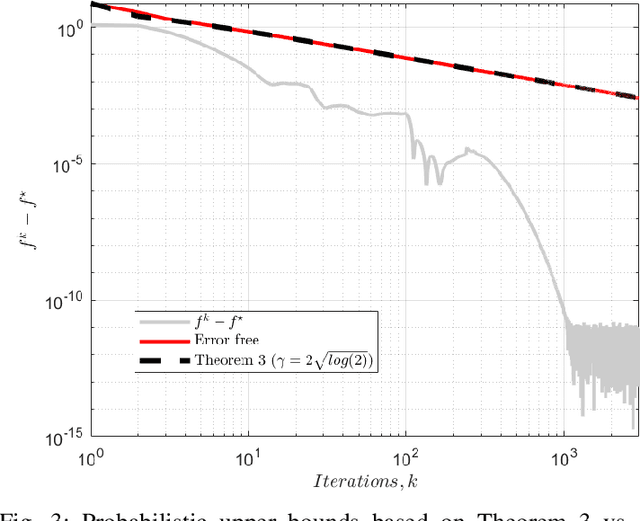
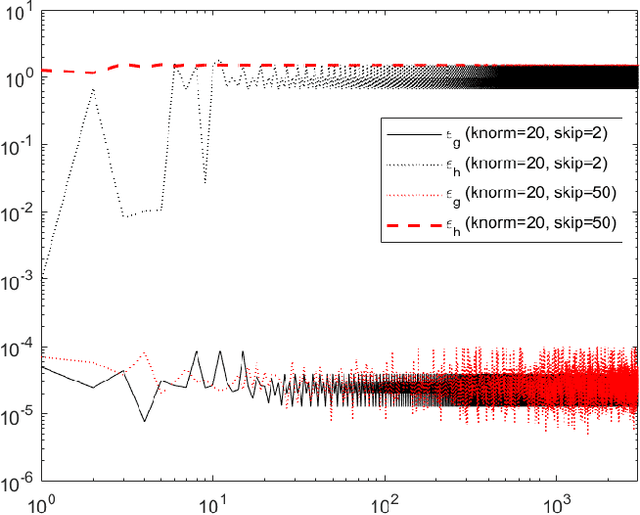
We analyse the convergence of an approximate, fully inexact, ADMM algorithm under additive, deterministic and probabilistic error models. We consider the generalized ADMM scheme that is derived from generalized Lagrangian penalty with additive (smoothing) adaptive-metric quadratic proximal perturbations. We derive explicit deterministic and probabilistic convergence upper bounds for the lower-C2 nonconvex case as well as the convex case under the Lipschitz continuity condition. We also present more practical conditions on the proximal errors under which convergence of the approximate ADMM to a suboptimal solution is guaranteed with high probability. We consider statistically and dynamically-unstructured conditional mean independent bounded error sequences. We validate our results using both simulated and practical software and algorithmic computational perturbations. We apply the proposed algorithm to a synthetic LASSO and robust regression with k-support norm regularization problems and test our proposed bounds under different computational noise levels. Compared to classical convergence results, the adaptive probabilistic bounds are more accurate in predicting the distance from the optimal set and parasitic residual error under different sources of inaccuracies.

Sharper Bounds for Proximal Gradient Algorithms with Errors

We analyse the convergence of the proximal gradient algorithm for convex composite problems in the presence of gradient and proximal computational inaccuracies. We derive new tighter deterministic and probabilistic bounds that we use to verify a simulated (MPC) and a synthetic (LASSO) optimization problems solved on a reduced-precision machine in combination with an inaccurate proximal operator. We also show how the probabilistic bounds are more robust for algorithm verification and more accurate for application performance guarantees. Under some statistical assumptions, we also prove that some cumulative error terms follow a martingale property. And conforming to observations, e.g., in \cite{schmidt2011convergence}, we also show how the acceleration of the algorithm amplifies the gradient and proximal computational errors.